Матрица математика как решать умножение

Узнайте, как использовать матрицы в математике для решения задач умножения. Получите подробное объяснение алгоритма умножения матриц и научитесь применять его в практике. Эта статья поможет вам улучшить свои навыки в математике и научиться решать сложные задачи с помощью матриц.

Умножение матриц – одна из основных операций в линейной алгебре. Оно позволяет умножать две матрицы и получать третью матрицу – результат их перемножения. В матричной алгебре это является важным инструментом для решения различных задач и моделирования различных процессов.

Чтобы правильно решать умножение матриц, необходимо следовать определенным правилам и алгоритмам. Сначала нужно убедиться, что количество столбцов в первой матрице равно количеству строк во второй матрице, иначе умножение невозможно. Затем происходит поэлементное умножение строк первой матрицы на столбцы второй, а результат суммируется. Таким образом, каждый элемент матрицы-результата является скалярным произведением соответствующих строк и столбцов.

Умножение матриц позволяет решать широкий спектр задач, таких как трансформация координат, решение систем линейных уравнений, моделирование физических и экономических процессов. Кроме того, оно является основой для других операций, таких как возведение матрицы в степень и нахождение обратной матрицы.

Важно отметить, что умножение матриц не коммутативно, то есть AB не всегда равно BA. Это означает, что порядок умножения имеет значение и может существенно влиять на результат.

Правильное решение умножения матриц – основа для получения точных результатов и успешного применения матричной алгебры в практике. Понимание основных правил и алгоритмов поможет вам эффективно решать задачи и достигать желаемых результатов.

Матрица математика: общая информация

Матрицы часто используются для передачи и обработки данных в различных областях науки, техники и экономики. Они могут быть использованы для описания связей между объектами, решения систем линейных уравнений, преобразования геометрических фигур, анализа данных и многих других задач.

Матрицы имеют свои особенности и свойства, которые позволяют проводить различные операции с ними. Например, умножение матриц, сложение матриц, нахождение определителя и ранга матрицы, нахождение обратной матрицы и т.д.

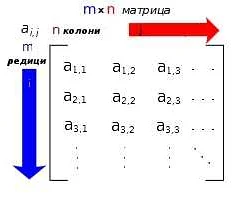
Матрицы могут быть заданы различными способами: в виде таблицы, в виде формулы или в виде списка элементов. Количество строк и столбцов в матрице называется ее размерностью, и она обозначается числом строк и столбцов через запятую.

Основные типы матриц — это квадратные матрицы, прямоугольные матрицы, нулевые матрицы, единичные матрицы и диагональные матрицы. Каждый тип матрицы имеет свои особенности и свойства, которые используются при решении математических задач.

Матрицы играют важную роль в различных областях математики, физики, экономики, компьютерных наук и других наук, и их изучение является неотъемлемой частью математического образования и исследований.

Что такое матрица в математике?

Матрица обычно записывается в виде прямоугольной сетки, где строки представляют собой горизонтальные линии, а столбцы — вертикальные линии. Каждый элемент матрицы находится на пересечении строки и столбца и имеет свой индекс, указывающий его положение.

Матрицы широко применяются в различных областях математики, физики, экономики, компьютерных наук и других науках. Они используются для решения систем линейных уравнений, описания линейных преобразований, моделирования данных и многих других задач.

Каждая матрица имеет свои особенности, такие как размерность (количество строк и столбцов), тип элементов (числа, булевы значения, символы и т.д.), способ задания и операции, которые можно выполнять с ней. Например, сложение, умножение, транспонирование, нахождение определителя и обратной матрицы.

Важно отметить, что для умножения матрицы на другую матрицу, необходимо соблюдать определенные правила и условия, в противном случае результат может быть некорректным. Также можно использовать специальные методы и алгоритмы для решения задач, связанных с матрицами.

В заключение, матрица является мощным инструментом в математике, который позволяет представлять и обрабатывать данные в удобной форме. Она является основой для решения сложных математических задач и имеет широкий спектр применения в различных областях науки и техники.

Основные операции с матрицами

Основные операции с матрицами включают:

1. Сложение матриц. Для сложения матриц они должны быть одинакового размера. Каждый элемент результирующей матрицы получается путем сложения соответствующих элементов слагаемых матриц.

2. Вычитание матриц. Для вычитания матриц они также должны быть одинакового размера. Каждый элемент результирующей матрицы получается путем вычитания соответствующих элементов вычитаемой матрицы из элементов уменьшаемой матрицы.

3. Умножение матрицы на число. Эта операция заключается в умножении каждого элемента матрицы на заданное число.

4. Умножение матриц. Умножение двух матриц возможно, если количество столбцов первой матрицы равно количеству строк второй матрицы. При умножении матриц получается новая матрица, количество строк которой равно количеству строк первой матрицы, а количество столбцов равно количеству столбцов второй матрицы. Каждый элемент результирующей матрицы получается путем умножения соответствующих элементов строк первой матрицы на соответствующие элементы столбцов второй матрицы и сложения полученных произведений.

5. Транспонирование матрицы. Транспонирование матрицы заключается в замене строк на столбцы. При транспонировании матрицы ее размеры меняются: количество строк становится равным количеству столбцов, и наоборот.

Операции с матрицами могут быть полезными при решении систем линейных уравнений, нахождении обратной матрицы, нахождении собственных значений и векторов и других математических задачах.

ОперацияОбозначение

Сложение матриц	А + B
Вычитание матриц	А — B
Умножение матрицы на число	α * A
Умножение матриц	A * B
Транспонирование матрицы	AT

Умножение матриц: основные правила

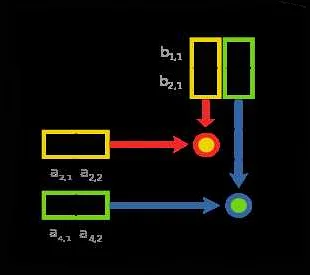
1. Размерность матриц. Для умножения матриц их размерности должны быть согласованы. Если у нас есть матрица A размером m x n и матрица B размером n x p, то мы можем умножить их, и результирующая матрица будет размером m x p.

2. Формула умножения. Для каждого элемента результирующей матрицы C[i][j] мы берем i-ую строку из матрицы A и j-ый столбец из матрицы B и умножаем соответствующие элементы их строк и столбцов, а затем суммируем эти произведения.

3. Порядок умножения. Умножение матриц не коммутативно, то есть порядок умножения имеет значение. Умножение матрицы A на матрицу B не равно умножению матрицы B на матрицу A.

4. Умножение на единичную матрицу. Умножение любой матрицы на единичную матрицу дает исходную матрицу. Единичная матрица представляет собой квадратную матрицу, у которой все диагональные элементы равны 1, а все остальные элементы равны 0.

5. Умножение на нулевую матрицу. Умножение любой матрицы на нулевую матрицу дает нулевую матрицу. Нулевая матрица представляет собой матрицу, у которой все элементы равны 0.

6. Ассоциативность умножения. Умножение матриц ассоциативно, то есть при умножении трех матриц A, B и C, результат будет одинаковым независимо от порядка умножения: (A * B) * C = A * (B * C).

7. Дистрибутивность умножения. Умножение матриц дистрибутивно относительно сложения, то есть (A + B) * C = A * C + B * C.

Умножение матриц — это мощный инструмент, который находит применение в различных областях, таких как физика, экономика, компьютерная графика и многое другое. Правильное применение правил умножения матриц позволяет получить точный результат и эффективно работать с данными.

Как решать умножение матриц?

Для умножения матриц необходимо соблюдать определенные правила. Пусть даны две матрицы: матрица A размером m x n и матрица B размером n x p. Результатом умножения данных матриц будет матрица C размером m x p.

Для получения элемента cij матрицы C необходимо умножить соответствующие элементы i-й строки матрицы A на j-й столбец матрицы B и сложить полученные произведения.

Матричное умножение можно записать следующим образом:

cij = ai1b1j + ai2b2j + … + ainbnj

Таким образом, для умножения матрицы A на матрицу B нужно выполнить операцию умножения для каждого элемента матрицы C.

Важно обратить внимание на согласованность размеров матриц. Количество столбцов матрицы A должно быть равно количеству строк матрицы B.

Умножение матриц важно для решения различных математических задач. Оно позволяет моделировать сложные системы и решать линейные уравнения. Также оно является основой для других матричных операций, таких как нахождение обратной матрицы и решение систем линейных уравнений.

Вывод: умножение матриц – это важная операция в математике, которая позволяет объединять различные значения и данные для получения новой информации. Правильное выполнение умножения матриц требует согласованности размеров матриц и правильного использования формулы умножения.

Практические примеры умножения матриц

Рассмотрим несколько примеров умножения матриц:

Пример 1:

2	3	1
4	2	5

Умножим эту матрицу на следующую:

1	2
3	4
5	6

Чтобы получить результат умножения, нужно каждый элемент первой строки первой матрицы умножить на соответствующий элемент первого столбца второй матрицы, а затем сложить полученные произведения. Таким образом, получим следующую матрицу:

20	28
29	46

Пример 2:

Умножим следующую матрицу:

1	2
3	4

На эту матрицу:

5	6
7	8

Результат умножения будет:

19	22
43	50

Таким образом, практические примеры умножения матриц позволяют наглядно продемонстрировать применение данной операции и получить точные результаты, которые могут быть использованы для решения различных задач.

Как получить точный результат при умножении матриц?

Для получения точного результата при умножении матриц необходимо учитывать следующие моменты:

1. Убедитесь, что размерности матриц совместимы. Матрица A размерности m×n может быть умножена на матрицу B размерности n×p только в том случае, если количество столбцов матрицы A равно количеству строк матрицы B.

2. Используйте корректную формулу умножения матриц. Результатом умножения матриц A и B будет новая матрица C, размерность которой будет равна m×p. Каждый элемент матрицы C вычисляется по формуле:

Cij = Ai1 · B1j + Ai2 · B2j + … + Ain · Bnj

где i принимает значения от 1 до m, j – от 1 до p, и n – количество столбцов матрицы A (или количество строк матрицы B).

3. При умножении матрицы на вектор или на скаляр, учтите, что размерности соответствуют правилам умножения матриц. Например, умножение матрицы размерности m×n на вектор размерности n×1 даст вектор размерности m×1.

4. Используйте точные числа при вычислении элементов матрицы C. Это особенно важно при работе с дробями или числами с плавающей точкой, чтобы избежать ошибок округления.

Соблюдение этих правил и методов поможет получить точный результат при умножении матриц и использовать его для решения широкого спектра задач в линейной алгебре и науке.

Вопрос-ответ:

Зачем нужно умножение матриц?

Умножение матриц используется в различных областях математики, физики, экономики и компьютерных наук. Эта операция позволяет комбинировать и совмещать различные данные и информацию, а также преобразовывать системы уравнений и решать сложные задачи.

Как умножать матрицы?

Для умножения матриц необходимо соблюдать определенные правила. Нужно убедиться, что количество столбцов первой матрицы равно количеству строк второй матрицы. Затем производится перемножение элементов исходных матриц, при этом элемент новой матрицы получается как сумма произведений элементов соответствующих строки первой матрицы и столбца второй матрицы.

Как проверить правильность результата умножения матриц?

Правильность результата умножения матриц можно проверить с помощью простой проверки. Для этого нужно умножить исходные матрицы в обратном порядке и сравнить полученный результат с исходными матрицами. Если результаты совпадают, то умножение было выполнено правильно.

Какие особенности есть при умножении матриц?

При умножении матриц существуют несколько особенностей, которые стоит учитывать. Например, умножение матриц не коммутативно, то есть AB не всегда равно BA. Также важно помнить, что размерность результирующей матрицы зависит от размерности исходных матриц, и некоторые матрицы не могут быть умножены вообще.

Видео по теме: