Что такое матрица в высшей математике простыми словами
Содержимое
- 1 Что такое матрица в высшей математике простыми словами
- 1.1 Что такое матрица в высшей математике?
- 1.2 Видео по теме:
- 1.3 Определение и основные понятия
- 1.4 Структура и элементы матрицы
- 1.5 Операции с матрицами
- 1.6 Примеры использования матриц
- 1.7 Матрицы в линейной алгебре
- 1.8 Матрицы в теории вероятностей
- 1.9 Применение матриц в компьютерной графике
- 1.10 Вопрос-ответ:
- 1.10.0.1 Зачем нужны матрицы в высшей математике?
- 1.10.0.2 Каково определение матрицы в высшей математике?
- 1.10.0.3 Как записывают матрицы?
- 1.10.0.4 Какие операции можно выполнять с матрицами?
- 1.10.0.5 Можете привести пример использования матриц в реальной жизни?
- 1.10.0.6 Что такое матрица?
- 1.10.0.7 Какие бывают типы матриц?
Матрица в высшей математике представляет собой таблицу чисел или выражений, упорядоченных в определенном порядке. Она используется для решения систем линейных уравнений, преобразований координат и многих других задач. В этой статье вы узнаете, что такое матрица и как она применяется в высшей математике.
Матрица – это одна из ключевых концепций высшей математики, которая играет важную роль во многих областях науки и техники. Она представляет собой упорядоченный набор чисел, расположенных в виде прямоугольной таблицы. В математической терминологии такая таблица называется матрицей, а числа в ней – элементами матрицы.
Каждый элемент матрицы имеет свою позицию, которая определяется номером строки и номером столбца, на пересечении которых он находится. Обозначение элемента матрицы производится с помощью индексов, например, aij, где i – номер строки, а j – номер столбца.
Матрицы широко используются в алгебре, анализе, теории вероятностей, физике, экономике и других научных дисциплинах. Они позволяют удобно описывать и решать различные математические и физические задачи, связанные с линейными операциями и системами уравнений.
Примером матрицы может служить таблица оценок студентов, где каждая строка соответствует определенному студенту, а каждый столбец – определенному предмету. Значения в ячейках таблицы представляют оценки студентов по соответствующим предметам.
Что такое матрица в высшей математике?
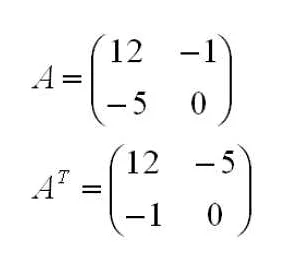
Матрицы можно представить как набор векторов, где каждый вектор является строкой или столбцом матрицы. Количество строк и столбцов определяет размерность матрицы. Например, матрица размерности 3×3 имеет 3 строки и 3 столбца.
Элементы матрицы могут быть любого типа данных: числа, буквы, символы и т.д. Они обычно обозначаются заглавными буквами, например, A, B, C, и так далее. Каждый элемент матрицы имеет свой индекс, который указывает его положение в строке и столбце.
Примером матрицы может служить матрица коэффициентов системы линейных уравнений:
A = | 2 3 |
| 4 5 |
В данном примере матрица A имеет размерность 2×2 и содержит элементы 2, 3, 4 и 5. Элемент A1,2 равен 3, так как он находится в первой строке и втором столбце.
Матрицы играют важную роль в решении систем линейных уравнений, нахождении определителей, нахождении собственных значений и векторов, а также многих других математических операций.
Вывод: Матрица – это таблица чисел, упорядоченных по строкам и столбцам. Она широко применяется в различных областях математики и имеет множество приложений.
Видео по теме:
Определение и основные понятия
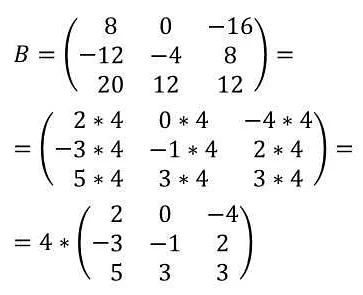
Основные понятия, связанные с матрицами:
Размерность матрицы — это количество строк и столбцов, которые она содержит. Обозначается двумя числами: M — количество строк, и N — количество столбцов. Матрица размерности MxN имеет M строк и N столбцов.
Элемент матрицы — это числовое значение, находящееся на пересечении строки и столбца. Обозначается символом aij, где i — номер строки, а j — номер столбца.
Главная диагональ — это последовательность элементов, которые находятся на одной линии от левого верхнего угла до правого нижнего угла матрицы. Элементы главной диагонали имеют одинаковые индексы i и j.
Транспонированная матрица — это матрица, полученная из исходной матрицы путем замены строк на столбцы и столбцов на строки. Обозначается символом AT.
Единичная матрица — это квадратная матрица, у которой все элементы на главной диагонали равны 1, а остальные элементы равны 0. Обозначается символом E.
Это основные понятия, которые помогают понять суть матриц в высшей математике.
Структура и элементы матрицы

Каждый элемент матрицы обозначается с помощью индексов. Индексы состоят из двух чисел: первое число указывает на номер строки, а второе число — на номер столбца, в котором находится элемент.
Например, матрица размерности 3×3 будет выглядеть следующим образом:
| a11 | a12 | a13 |
| a21 | a22 | a23 |
| a31 | a32 | a33 |
Здесь aij — элемент матрицы, где i — номер строки, а j — номер столбца.
Матрицы могут быть различных типов: квадратные, прямоугольные, нулевые, единичные и другие. Также в матрицах могут быть определены операции сложения, умножения, транспонирования и другие.
Операции с матрицами
Матрицы подчиняются определенным операциям, которые позволяют выполнять различные действия с этими структурами данных. Рассмотрим основные операции с матрицами:
- Сложение матриц — это операция, при которой суммируются соответствующие элементы матриц. Для сложения матриц необходимо, чтобы они имели одинаковое количество строк и столбцов.
- Умножение матриц — это операция, при которой каждый элемент новой матрицы вычисляется как сумма произведений элементов соответствующих строки первой матрицы на элементы соответствующего столбца второй матрицы.
- Умножение матрицы на число — это операция, при которой каждый элемент матрицы умножается на заданное число.
- Транспонирование матрицы — это операция, при которой строки матрицы становятся столбцами, а столбцы — строками.
- Определитель матрицы — это число, которое связано с матрицей и позволяет определить, является ли матрица обратимой.
- Обратная матрица — это такая матрица, при умножении которой на исходную матрицу получается единичная матрица.
Это лишь некоторые из операций с матрицами. Они играют важную роль в высшей математике и находят применение в различных областях науки и техники.
Примеры использования матриц
Матрицы широко применяются в различных областях математики, физики, компьютерной графики, экономики и других науках. Вот несколько примеров использования матриц:
1. Линейные преобразования
Матрицы используются для представления линейных преобразований, таких как повороты, масштабирование и смещение в трехмерном пространстве. Например, матрица поворота может быть использована для изменения ориентации объекта в трехмерном пространстве.
2. Решение систем линейных уравнений
Матрицы используются для решения систем линейных уравнений. Каждое уравнение представляется в виде строки матрицы, а неизвестные значения – в виде столбца. Затем система уравнений может быть решена с помощью метода Гаусса или других методов.
3. Криптография
Матрицы используются в криптографии для шифрования информации. Например, матрицы могут быть использованы для перемешивания символов в тексте или для умножения на вектор, чтобы зашифровать сообщение.
4. Компьютерная графика
Матрицы используются в компьютерной графике для преобразования трехмерных объектов в двумерное изображение на экране. Например, матрица проекции может быть использована для преобразования координат вершин трехмерного объекта в двумерные координаты на экране.
5. Статистика
Матрицы используются в статистике для анализа данных. Например, матрица корреляции может быть использована для определения степени взаимосвязи между различными переменными.
Все эти примеры демонстрируют важность матриц в решении различных задач и их широкое применение в реальном мире.
Матрицы в линейной алгебре
Матрица состоит из элементов, которые располагаются в ячейках, образующих строки и столбцы. Каждый элемент матрицы обозначается в виде aij, где i — номер строки, а j — номер столбца. Например, матрица размером 2×3 будет иметь вид:
| a11 | a12 | a13 |
| a21 | a22 | a23 |
Матрицы могут быть разных типов, в зависимости от их размерности и свойств элементов. Например, квадратная матрица имеет одинаковое количество строк и столбцов, прямоугольная матрица имеет разное количество строк и столбцов, а нулевая матрица состоит из всех нулей.
Матрицы могут быть сложены, умножены на число, умножены друг на друга и обратимы. Определенные операции над матрицами позволяют решать системы линейных уравнений, находить собственные значения и векторы, а также применять преобразования координат и векторов.
Примеры матриц в линейной алгебре:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
или
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Матрицы в теории вероятностей
Матрицы имеют широкое применение в различных областях математики, включая теорию вероятностей. В теории вероятностей матрицы используются для описания и анализа вероятностных моделей и стохастических процессов.
Одним из основных примеров использования матриц в теории вероятностей являются матрицы переходных вероятностей. Эти матрицы используются для описания перехода между состояниями в стохастических процессах. Каждый элемент матрицы представляет собой вероятность перехода из одного состояния в другое.
Например, рассмотрим простую модель марковского процесса с двумя состояниями: «солнечно» и «дождливо». Матрица переходных вероятностей для этой модели может выглядеть следующим образом:
- Если сейчас «солнечно», то с вероятностью 0.8 будет «солнечно» и с вероятностью 0.2 будет «дождливо».
- Если сейчас «дождливо», то с вероятностью 0.3 будет «солнечно» и с вероятностью 0.7 будет «дождливо».
Такая матрица позволяет описывать вероятности перехода между состояниями в каждый момент времени и анализировать вероятностные свойства процесса.
В теории вероятностей также используются другие виды матриц, например, матрицы условных вероятностей, матрицы распределения вероятностей и т. д. Все они играют важную роль в анализе случайных процессов и моделировании вероятностных явлений.
Применение матриц в компьютерной графике
Матрицы играют важную роль в компьютерной графике. Они позволяют задавать и преобразовывать различные геометрические объекты, такие как точки, линии и фигуры. С помощью матриц можно выполнять такие операции, как масштабирование, поворот, сдвиг и отражение объектов.
Одним из основных применений матриц в компьютерной графике является преобразование координат. Координаты точек на экране могут быть представлены с помощью матрицы, что позволяет легко изменять их расположение, направление и масштаб.
Например, чтобы выполнить масштабирование объекта, можно использовать матрицу масштабирования. Эта матрица изменяет размеры объекта вдоль каждой из осей x и y. Аналогично, для поворота объекта можно использовать матрицу поворота, которая изменяет направление объекта на определенный угол.
Матрицы также применяются для преобразования цветовых значений. Каждый пиксель на экране может быть представлен как комбинация красного, зеленого и синего цветов, известных как RGB. С помощью матриц можно изменять интенсивность каждого цвета, создавая эффекты, такие как оттенки, тени и градиенты.
Кроме того, матрицы используются для комбинирования различных преобразований. Например, можно сначала выполнить масштабирование и затем повернуть объект. Для этого необходимо умножить матрицы масштабирования и поворота. Такой подход позволяет создавать сложные и реалистичные эффекты в компьютерной графике.
- Преобразование координат
- Масштабирование объектов
- Поворот объектов
- Изменение цветовых значений
- Комбинирование преобразований
Вопрос-ответ:
Зачем нужны матрицы в высшей математике?
Матрицы являются важным инструментом в высшей математике, так как они позволяют компактно и удобно записывать и решать системы линейных уравнений, находить собственные значения и собственные векторы линейных операторов, а также решать множество других задач. Благодаря матрицам можно сделать множество вычислений более эффективными и удобными.
Каково определение матрицы в высшей математике?
Матрица — это упорядоченный набор чисел, расположенных в виде прямоугольной таблицы. Матрицы имеют размерность, которая задается количеством строк и столбцов. Например, матрица размерности 3×2 содержит 3 строки и 2 столбца.
Как записывают матрицы?
Матрицы обычно записывают с помощью квадратных скобок. Каждая строка матрицы записывается через запятую, а между элементами строки ставится пробел. Например, матрица размерности 2×3 может быть записана следующим образом: [1 2 3; 4 5 6]. Первая строка матрицы содержит элементы 1, 2 и 3, а вторая строка — элементы 4, 5 и 6.
Какие операции можно выполнять с матрицами?
С матрицами можно выполнять различные операции, такие как сложение, вычитание, умножение на число, умножение матрицы на матрицу. Например, сложение матриц происходит покомпонентно, то есть каждый элемент результирующей матрицы равен сумме соответствующих элементов слагаемых матриц. Умножение матриц осуществляется по определенным правилам и позволяет получить новую матрицу.
Можете привести пример использования матриц в реальной жизни?
Одним из примеров использования матриц в реальной жизни является задача оптимизации процессов. Например, при планировании производства товаров можно использовать матрицы для определения оптимального распределения ресурсов и минимизации затрат. Также матрицы широко применяются в компьютерной графике для трансформации и манипуляции объектами.
Что такое матрица?
Матрица — это упорядоченная прямоугольная таблица чисел или символов, разделенных на строки и столбцы. Она используется для представления данных и решения математических задач. Например, матрицы используются для описания линейных уравнений, преобразований векторов и многих других математических операций.
Какие бывают типы матриц?
Существует несколько типов матриц, включая квадратные, прямоугольные, треугольные, диагональные и единичные. Квадратная матрица имеет одинаковое количество строк и столбцов, прямоугольная матрица имеет разное количество строк и столбцов, треугольная матрица имеет нулевые элементы либо выше, либо ниже главной диагонали, диагональная матрица имеет ненулевые элементы только на главной диагонали, а единичная матрица имеет ненулевые элементы только на главной диагонали и равны единицам.
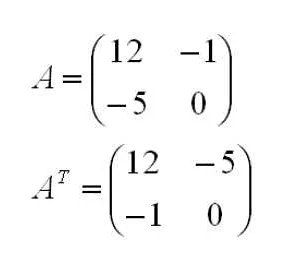


Статья очень понятно и доступно объясняет, что такое матрица в высшей математике. Наконец-то я разобралась с этим понятием! Примеры, которые приведены в статье, помогли мне лучше понять, как использовать матрицы в практических задачах. Теперь я понимаю, что матрица — это таблица из чисел, которая помогает решать системы уравнений и проводить линейные преобразования. Очень рада, что такая сложная тема объяснена так простыми словами. Спасибо автору за четкое и понятное изложение материала!
Отличная статья! Я всегда хотела разобраться, что такое матрица в высшей математике, но боялась, что это будет сложно. Но благодаря вашему объяснению, все стало намного яснее. Теперь я понимаю, что матрица — это прямоугольная таблица, состоящая из чисел или символов. Кажется, что они действительно могут быть очень полезными в решении различных задач. Примеры, которые вы привели, помогли мне лучше представить, как матрицы работают на практике. Теперь я почувствовала себя немного математиком! Спасибо за простое и понятное объяснение!
Статья прекрасно раскрывает сущность матриц в высшей математике. Важно, что автор использует простые и понятные слова, что позволяет мне, как читателю, лучше понять основные концепции. Примеры также являются отличным дополнением, помогающим усвоить материал. Я теперь чувствую, что имею достаточное представление о матрицах и их применении в математике. Спасибо автору за интересную и познавательную статью!