Математическая матрица для чего она нужна
Содержимое
- 1 Математическая матрица для чего она нужна
- 1.1 Математическая матрица: устройство и свойства
- 1.2 Видео по теме:
- 1.3 Определение и классификация матриц
- 1.4 Операции над матрицами: сложение и умножение
- 1.5 Вопрос-ответ:
- 1.5.0.1 Зачем нужна математическая матрица?
- 1.5.0.2 Какие применения имеет математическая матрица?
- 1.5.0.3 Какие операции можно выполнять с матрицами?
- 1.5.0.4 Как можно представить матрицу графически?
- 1.5.0.5 Какие свойства имеют матрицы?
- 1.5.0.6 Для чего используют математические матрицы?
- 1.5.0.7 Какие операции можно выполнять с матрицами?
- 1.6 Свойства матриц: симметричность и обратимость
- 1.7 Применение матриц в линейной алгебре
- 1.8 Матрицы в теории графов: представление и анализ
- 1.9 Матричные методы в статистике и экономике
- 1.10 Матрицы в компьютерной графике и компьютерных играх
- 1.11 Применение матриц в машинном обучении и искусственном интеллекте
Математическая матрица — это удобный инструмент для представления и решения различных математических задач. Узнайте, как она используется в линейной алгебре, графическом моделировании, статистике и других областях науки и техники.
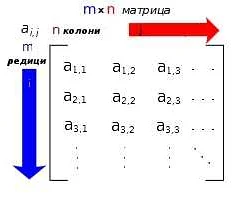
Матрица — это одна из ключевых структур данных в математике, которая используется для описания и решения различных задач. Она представляет собой таблицу, состоящую из элементов, упорядоченных по строкам и столбцам. Каждый элемент матрицы имеет свое значение и порядковый номер, что позволяет оперировать данными внутри матрицы и выполнять различные математические операции.
Назначение матрицы заключается в том, чтобы систематизировать и структурировать данные, а также в упрощении решения задач. Она может быть использована для описания линейных отношений, моделирования и решения систем уравнений, анализа данных и многих других задач. Матрица также является основой для различных алгоритмов и методов решения задач, включая матричные умножения, нахождение определителя и ранга матрицы, поиск собственных значений и векторов и т.д.
«Матрица — это мощный инструмент, который позволяет упорядочить и обрабатывать данные, а также решать различные задачи в математике и других областях науки и техники».
Применение матрицы находит широкое применение в различных областях, включая физику, экономику, компьютерную графику, машинное обучение, теорию вероятности и многих других. Она позволяет моделировать и анализировать различные процессы и системы, решать задачи оптимизации и прогнозирования, а также разрабатывать алгоритмы и программы для обработки данных и принятия решений. Благодаря своей универсальности и эффективности, матрица является неотъемлемой частью современной математики и науки в целом.
Математическая матрица: устройство и свойства
У матрицы есть несколько основных свойств:
- Размерность: матрица имеет определенное количество строк и столбцов. Ее размерность обозначается числом строк и числом столбцов.
- Элементы: каждый элемент матрицы представляет собой число, расположенное на определенной позиции в таблице.
- Структура: матрица состоит из строк и столбцов, которые пересекаются и образуют клетки. Каждая клетка содержит один элемент.
- Типы матриц: существуют различные типы матриц, такие как квадратная матрица, прямоугольная матрица, диагональная матрица и другие. Каждый тип матрицы имеет свои особенности и свойства.
- Операции: с помощью матриц можно выполнять различные математические операции, такие как сложение, вычитание, умножение и другие. Операции над матрицами позволяют решать различные задачи в математике, физике, экономике и других науках.
Математическая матрица является важным инструментом в математике и имеет широкое применение в различных областях. Она используется для решения систем линейных уравнений, нахождения собственных значений и собственных векторов, аппроксимации данных, обработки изображений и многих других задач.
Видео по теме:
Определение и классификация матриц
Математическая матрица представляет собой упорядоченный набор элементов, расположенных в виде прямоугольной таблицы, состоящей из строк и столбцов. Каждый элемент матрицы имеет свое место, которое определяется его положением в строке и столбце.
Матрицы часто используются для представления и решения различных математических задач. Они позволяют компактно хранить и обрабатывать большие объемы данных и удобно работать с линейными операциями, такими как сложение, умножение и нахождение обратной матрицы.
Матрицы можно классифицировать по различным характеристикам:
- По размерности: матрицы могут быть одномерными (векторами), двумерными (матрицами) или иметь большую размерность.
- По типу элементов: матрицы могут содержать элементы из различных множеств, например, числа, булевы значения или символы.
- По способу заполнения: матрицы могут быть заполнены определенным образом, например, нулями, случайными числами или значениями, полученными из других источников данных.
- По структуре: матрицы могут быть разреженными, когда большинство элементов равны нулю, или плотными, когда большинство элементов отличны от нуля.
Классификация матриц позволяет определить особенности их использования в различных областях науки, техники и экономики, а также выбрать подходящие методы и алгоритмы для работы с ними.
Операции над матрицами: сложение и умножение

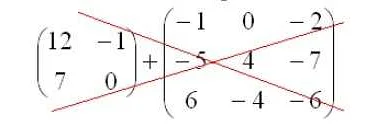
Сложение матриц производится путем покомпонентного сложения элементов матриц одинакового размера. Для того чтобы сложить две матрицы, необходимо, чтобы их размерности совпадали. Каждый элемент полученной матрицы равен сумме соответствующих элементов исходных матриц.
Умножение матриц является более сложной операцией. Размеры матриц должны соответствовать условию: количество столбцов первой матрицы должно быть равно количеству строк второй матрицы. Каждый элемент полученной матрицы вычисляется путем умножения элементов строки первой матрицы на соответствующие элементы столбца второй матрицы и их суммирования.
Умножение матриц является одной из основных операций в линейной алгебре и находит широкое применение в различных областях: от программирования и компьютерной графики до экономики и физики.
Операции над матрицами позволяют решать множество задач, связанных с обработкой данных и моделированием различных процессов.
Вопрос-ответ:
Зачем нужна математическая матрица?
Матрица — это удобный инструмент для хранения и обработки данных. Она позволяет компактно представить информацию, а также выполнять различные операции, такие как сложение, умножение и нахождение обратной матрицы.
Какие применения имеет математическая матрица?
Матрицы широко используются во многих областях, включая физику, экономику, информатику, статистику и многие другие. Они позволяют решать системы линейных уравнений, моделировать физические процессы, обрабатывать изображения и звук, анализировать данные и многое другое.
Какие операции можно выполнять с матрицами?
С матрицами можно выполнять множество операций. К ним относятся сложение и вычитание матриц, умножение матрицы на число, умножение матрицы на матрицу, нахождение обратной матрицы, нахождение определителя, решение систем линейных уравнений и многое другое.
Как можно представить матрицу графически?
Матрицу можно представить в виде прямоугольной таблицы, где каждый элемент матрицы располагается в ячейке таблицы. Количество строк и столбцов в таблице соответствует размерам матрицы. Также можно представить матрицу графически с помощью графов и схем.
Какие свойства имеют матрицы?
Матрицы обладают множеством свойств. Некоторые из них включают коммутативность сложения и умножения матриц, ассоциативность умножения матриц, существование нейтральных и обратных элементов относительно сложения и умножения, связь между определителем матрицы и ее свойствами, и многое другое.
Для чего используют математические матрицы?
Математические матрицы используются для решения различных задач в математике, физике, экономике и других областях науки. Они позволяют компактно представить и обрабатывать большие объемы данных и выполнять различные операции, такие как сложение, умножение, нахождение определителя и обратной матрицы.
Какие операции можно выполнять с матрицами?
С матрицами можно выполнять различные операции, такие как сложение, вычитание, умножение на число, умножение матрицы на матрицу, нахождение определителя, нахождение обратной матрицы и др. Операции с матрицами позволяют решать системы линейных уравнений, находить собственные значения и собственные векторы, проводить анализ данных и многое другое.
Свойства матриц: симметричность и обратимость
Два основных свойства матриц, которые часто изучаются, – это симметричность и обратимость.
Симметричность – это свойство матрицы, когда она равна транспонированной матрице, то есть элементы матрицы A[i][j] равны элементам матрицы A[j][i].
Для примера, рассмотрим матрицу:
1 2 3
2 4 5
3 5 6
Эта матрица является симметричной, так как она равна своей транспонированной матрице:
1 2 3 1 2 3
2 4 5 = 2 4 5
3 5 6 3 5 6
Обратимость – это свойство матрицы, когда существует обратная матрица, которая при умножении на исходную матрицу дает единичную матрицу.
Единичная матрица – это матрица, у которой все элементы на главной диагонали равны 1, а остальные элементы равны 0.
Для примера, рассмотрим матрицу:
1 2
3 4
Эта матрица обратима, так как существует обратная матрица:
-2 1
1.5 -0.5
При умножении исходной матрицы на обратную получаем единичную матрицу:
1 2 -2 1 1 0
3 4 * 1.5 -0.5 = 0 1
Симметричность и обратимость являются важными свойствами матриц, которые имеют различные применения в математике, физике, экономике и других областях науки.
Применение матриц в линейной алгебре
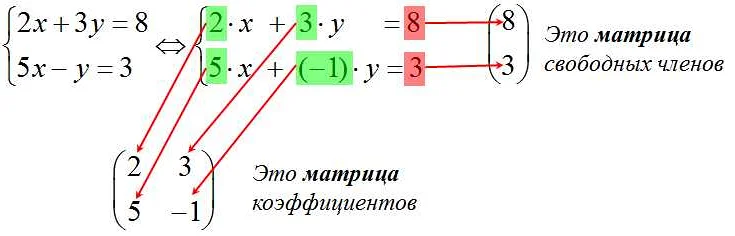
- Системы линейных уравнений. Матрицы позволяют компактно записывать системы линейных уравнений и решать их с помощью методов матричной алгебры, таких как метод Гаусса или метод Гаусса-Жордана.
- Линейные преобразования. Матрицы можно использовать для представления и анализа линейных преобразований, таких как повороты, масштабирования и сдвиги в трехмерном пространстве.
- Декомпозиция матриц. Матрицы могут быть разложены на более простые компоненты с помощью различных методов, таких как LU-разложение, QR-разложение и сингулярное разложение. Это позволяет решать системы линейных уравнений, находить обратные матрицы и находить собственные значения и собственные векторы.
- Определители. Матрицы позволяют вычислять определители, которые являются важными характеристиками матрицы и находят применение в различных задачах, например, при вычислении площади треугольника или объема параллелепипеда.
- Компьютерная графика. Матрицы используются для преобразования и отображения трехмерных объектов на двумерный экран. Например, матрицы проекции позволяют строить перспективные изображения.
- Теория вероятностей и статистика. Матрицы используются для описания и анализа случайных процессов и моделей, например, при построении матрицы переходных вероятностей или вычислении ковариационной матрицы.
Это лишь некоторые примеры применения матриц в линейной алгебре. Благодаря своей универсальности и эффективности, матрицы являются важным инструментом для решения различных задач в науке, технике и других областях знания.
Матрицы в теории графов: представление и анализ

Матрицы играют важную роль в теории графов, которая занимается изучением связей и взаимодействий между объектами, называемыми вершинами. В графовой теории существуют различные типы матриц, которые используются для представления графов и их анализа.
Одна из наиболее распространенных матриц, используемых в теории графов, — это матрица смежности. В этой матрице каждой вершине графа соответствует строка и столбец, а на пересечении строки и столбца стоит число, обозначающее наличие или отсутствие ребра между соответствующими вершинами. Если ребро есть, то число может быть равно 1 или любому другому положительному значению, а если ребра нет, то число может быть равно 0 или отрицательному значению.
Еще одной важной матрицей в теории графов является матрица инцидентности. В этой матрице каждой вершине и каждому ребру графа соответствует строка и столбец, а на пересечении строки и столбца стоит число, обозначающее связь между соответствующей вершиной и ребром. Если вершина является началом или концом ребра, то число может быть равно 1 или любому другому положительному значению, а если вершина не связана с ребром, то число может быть равно 0 или отрицательному значению.
Также в теории графов используется матрица достижимости, которая позволяет определить, существует ли путь между двумя вершинами графа. В этой матрице каждой паре вершин соответствует строка и столбец, а на пересечении строки и столбца стоит число, обозначающее наличие или отсутствие пути между соответствующими вершинами.
Матрицы в теории графов широко применяются для анализа свойств графов, таких как наличие циклов, связность, планарность и др. Они позволяют компактно представить информацию о графе и проводить различные операции над ним, такие как умножение матриц, возведение матриц в степень и др.
Таким образом, матрицы в теории графов играют важную роль, облегчая анализ и изучение графовых структур и их свойств.
Матричные методы в статистике и экономике
Матричные методы играют важную роль в статистике и экономике. Они позволяют анализировать данные и решать различные задачи, связанные с обработкой больших объемов информации.
В статистике матрицы используются для работы с многомерными статистическими данными. Например, с помощью матриц можно представить выборку данных, состоящую из нескольких переменных, и проводить их сравнительный анализ. Матрицы также используются при решении задач классификации и кластеризации, а также при построении регрессионных моделей.
В экономике матричные методы применяются для анализа экономических систем и моделирования экономических процессов. Матрицы используются для описания взаимосвязей между экономическими агентами, например, между производителями и потребителями. С помощью матриц можно анализировать структуру экономических секторов, определять устойчивость экономических систем, а также моделировать влияние различных факторов на экономические показатели.
Матричные методы также находят применение в других областях, таких как физика, биология, информатика и т. д. Они являются мощным инструментом для анализа и обработки данных, позволяют решать сложные задачи и получать новые знания о реальных системах.
Матрицы в компьютерной графике и компьютерных играх
Матрицы играют важную роль в компьютерной графике и компьютерных играх. Они используются для преобразования и трансформации объектов в трехмерном пространстве.
В компьютерной графике матрицы позволяют определить положение, поворот и масштаб объекта. С их помощью можно перемещать объекты, вращать их вокруг определенной оси, изменять их размеры. Таким образом, матрицы позволяют создавать анимацию и визуальные эффекты.
В компьютерных играх матрицы используются для определения положения и движения игровых объектов. Они позволяют контролировать перемещение игрока и других персонажей, определять коллизии и столкновения объектов, а также вычислять освещение и тени.
Одним из наиболее распространенных применений матриц в компьютерной графике и играх является проекция. Матрицы проекции позволяют отображать трехмерные объекты на двухмерный экран. С их помощью можно создавать эффект глубины и реалистичности визуального представления.
Использование матриц в компьютерной графике и компьютерных играх требует умения работать с математическими операциями и алгоритмами. Матричные вычисления позволяют достичь высокой степени реалистичности и детализации визуальных эффектов, создавая уникальные и захватывающие игровые миры.
Применение матриц в машинном обучении и искусственном интеллекте
Матрицы играют ключевую роль в области машинного обучения и искусственного интеллекта. Они предоставляют мощный инструмент для организации и обработки данных, которые используются для обучения моделей и принятия решений.
В машинном обучении матрицы широко применяются для представления данных. Например, в задачах классификации каждый объект может быть представлен в виде вектора, а набор таких векторов можно организовать в матрицу, где каждая строка соответствует объекту, а каждый столбец — признаку. Такая матрица данных может быть использована для обучения модели классификации.
Матрицы также применяются для преобразования данных и выявления скрытых закономерностей. С помощью операций над матрицами можно сжать информацию, выделить наиболее значимые признаки и устранить шум. Эти процессы, называемые факторным анализом и снижением размерности, помогают улучшить качество моделей и упростить интерпретацию результатов.
В искусственном интеллекте матрицы применяются для организации знаний и представления логических связей. Например, матрицы смежности используются для представления графов, где каждый элемент матрицы указывает наличие или отсутствие ребра между вершинами. Это позволяет эффективно решать задачи поиска кратчайшего пути, кластеризации и рекомендации.
Матрицы также являются основой для обучения нейронных сетей — распространенного подхода в области искусственного интеллекта. Каждый слой нейронной сети представляет собой матрицу весов, а операции над этими матрицами позволяют модели аппроксимировать сложные функции и решать широкий спектр задач.
Таким образом, матрицы играют важную роль в машинном обучении и искусственном интеллекте, обеспечивая эффективное представление и обработку данных, а также возможность принятия обоснованных решений на основе этих данных.

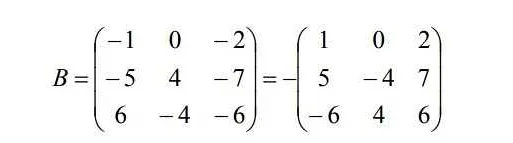
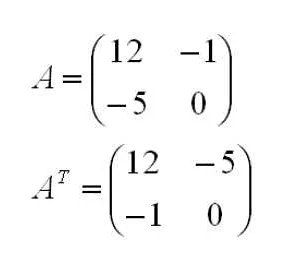

Очень интересная статья про математические матрицы! Я всегда задавалась вопросом, для чего они нужны и как применяются. Оказывается, матрицы используются во многих областях, начиная от физики и экономики и заканчивая программированием и компьютерной графикой. Я узнала, что матрицы позволяют компактно представлять и обрабатывать большие объемы данных. Например, в компьютерной графике они используются для преобразования и перемещения объектов на экране. Это позволяет создавать реалистичные и динамичные изображения. Также матрицы применяются в статистике и экономике для анализа данных и моделирования различных явлений. Они помогают решать сложные задачи оптимизации и прогнозирования. Я бы хотела узнать больше о применении матриц в моей профессиональной области. Например, как они могут быть полезны в маркетинге или управлении проектами. В целом, статья очень понятно объясняет, что такое математическая матрица и зачем она нужна. Я узнала много нового и получила стимул изучать эту тему глубже. Большое спасибо автору за интересную и познавательную статью!
Замечательная статья! Я всегда увлекалась математикой, и в особенности мне нравится работа с матрицами. Матрицы — это мощный инструмент, который применяется в различных областях знаний, от физики и экономики до компьютерной графики и машинного обучения. Одним из основных назначений матриц является решение систем линейных уравнений. Благодаря матрицам можно эффективно и точно находить решения для систем с большим количеством переменных. Кроме того, матрицы используются в геометрии для преобразования и вращения объектов. Я также узнала, что матрицы имеют важное значение в компьютерной графике. Они используются для преобразования трехмерных моделей, применения текстур и освещения. Без матриц визуализация объектов была бы гораздо сложнее и медленнее. Интересно, что матрицы широко применяются в машинном обучении. Они используются для обработки данных, построения моделей и решения задач классификации. Без матриц было бы сложно представить себе работу нейронных сетей и алгоритмов машинного обучения. В целом, матрицы — это мощный инструмент, который находит свое применение во многих областях науки и техники. Они помогают нам решать сложные задачи и находить оптимальные решения. Я рада, что узнала больше о матрицах благодаря этой статье!