Что такое минор высшая математика
Содержимое
- 1 Что такое минор высшая математика
Минор в высшей математике — это дополнительное специализированное направление в рамках математической науки. Статья расскажет о том, что такое минор в математике, его применение и значимость в современном мире. Узнайте, каким образом миноры используются в различных областях науки и техники, и как они способствуют развитию математического мышления и решению сложных задач.
Минор — это одно из основных понятий в высшей математике, которое широко применяется в различных областях, включая линейную алгебру, теорию матриц и дифференциальные уравнения. Минор представляет собой определенный определитель, вычисляемый для определенной подматрицы матрицы.
Основное назначение миноров в математике — это анализ и изучение свойств матрицы. Они позволяют определить, является ли матрица невырожденной (обратимой) или вырожденной (необратимой), а также выявить линейную зависимость или независимость векторов, которые представлены матрицей.
Миноры имеют широкое применение во многих областях науки и техники. Они используются в физике, экономике, компьютерной графике и других дисциплинах для решения различных задач, таких как определение стабильности системы, нахождение собственных значений и векторов, а также для решения систем линейных уравнений.
Примечание: Миноры также являются важным инструментом в теории графов, где они позволяют анализировать связи между вершинами и ребрами графа.
Таким образом, миноры являются неотъемлемой частью высшей математики и играют важную роль в решении широкого спектра математических и прикладных задач. Их определение и применение являются важными темами для изучения студентами и исследователями в области математики и ее приложений.
Что такое минор высшая математика

Минором матрицы называется определитель квадратной подматрицы, полученной из исходной матрицы путем выбора определенных строк и столбцов.
Миноры играют важную роль в решении систем линейных уравнений, нахождении собственных значений и векторов матрицы, а также в других задачах алгебры и анализа.
Определение и вычисление миноров матрицы требует знания теории определителей, линейной алгебры и матричных операций.
Использование миноров позволяет сократить размерность задачи и облегчить алгебраические вычисления.
В итоге, знание миноров и их применение позволяет математикам эффективно работать с крупными системами уравнений и сложными матрицами.
Видео по теме:
Определение минора в высшей математике
Другими словами, минор матрицы — это определитель матрицы, образованной выбором нескольких строк и столбцов исходной матрицы. При этом выбранные строки и столбцы образуют квадратную подматрицу.
Миноры матрицы используются для исследования ее свойств, решения систем уравнений, нахождения собственных значений и векторов, а также в других областях математики и ее приложений.
Определение и изучение миноров позволяет получить информацию о матрице и ее свойствах, а также применять их в различных математических моделях и задачах.
Применение миноров в высшей математике

- Линейная алгебра: Миноры используются для решения систем линейных уравнений, определения ранга матрицы и нахождения обратной матрицы. Они помогают анализировать свойства матриц и выполнять операции с ними.
- Теория графов: Миноры применяются для изучения графов и их свойств. Они позволяют определить, является ли граф планарным, ациклическим или связным. Также они используются в задачах о раскраске графов и поиске минимального остовного дерева.
- Теория вероятностей: Миноры применяются для вычисления вероятности событий и исследования зависимостей между случайными величинами. Они помогают определить условную вероятность и выполнить различные статистические анализы.
- Математическая физика: В задачах математической физики миноры используются для нахождения собственных значений и собственных функций дифференциальных операторов. Они также применяются для решения уравнения Лапласа и других уравнений математической физики.
- Дифференциальные уравнения: Миноры применяются для изучения свойств и решения дифференциальных уравнений. Они помогают определить тип уравнения, найти общее решение или частное решение уравнения.
Это лишь некоторые примеры применения миноров в высшей математике. Они играют важную роль в анализе данных, моделировании и решении различных задач. Понимание миноров позволяет математикам эффективно работать с разнообразными математическими структурами и находить новые решения и результаты.
Как найти минор в матрице
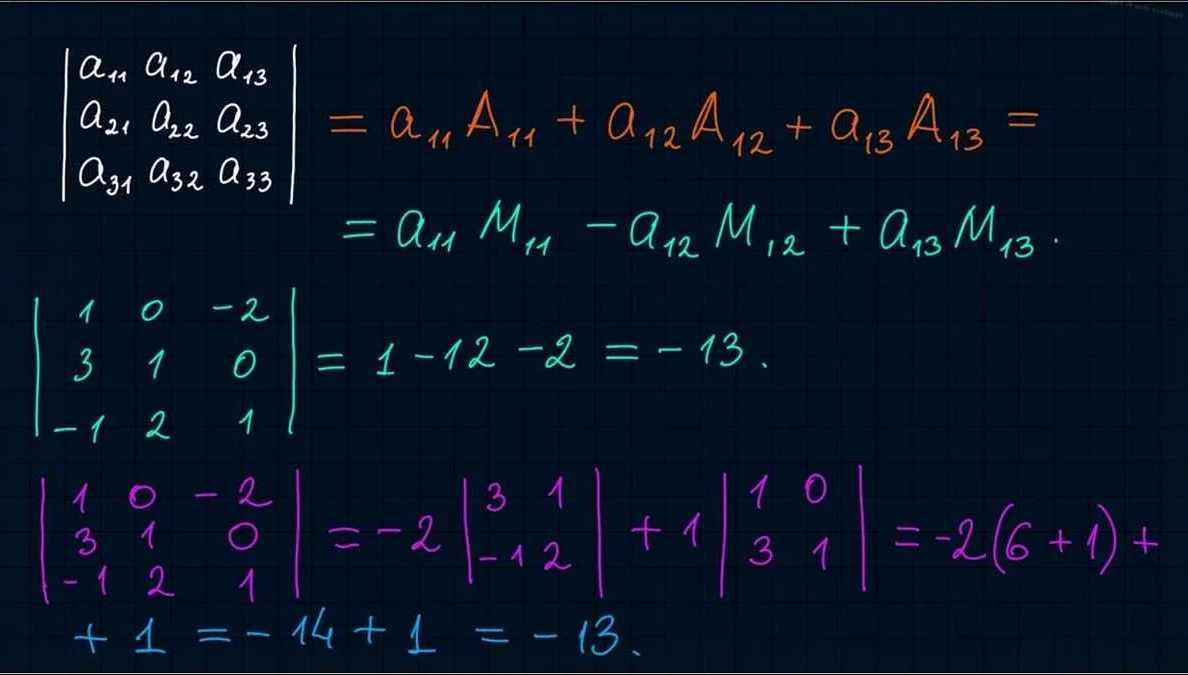
Для нахождения минора в матрице нужно выбрать квадратную подматрицу по определённым правилам:
- Выбираем k строк и k столбцов исходной матрицы, где k – размерность минора.
- Исключаем выбранные строки и столбцы, оставляя только остальные элементы.
После этого находим определитель получившейся матрицы – это и будет минором исходной матрицы.
Миноры широко применяются в линейной алгебре и математическом анализе. Они используются для решения систем линейных уравнений, нахождения обратной матрицы, определения ранга матрицы и других задач.
Свойства миноров в высшей математике

Существуют несколько свойств миноров, которые помогают в их использовании:
1. Замена строк или столбцов. Если строки или столбцы матрицы заменить соответствующими линейными комбинациями, миноры не изменятся.
2. Замена элементов. Если элементы матрицы заменить на их линейные комбинации, миноры также не изменятся.
3. Умножение строки или столбца на константу. Если строку или столбец матрицы умножить на некоторую константу, определитель минора будет умножаться на эту же константу.
4. Добавление строки или столбца. Если к строке или столбцу матрицы добавить линейную комбинацию других строк или столбцов, миноры не изменятся.
5. Связь с определителем. Миноры связаны с определителем основной матрицы. Если миноры одной строки или столбца матрицы равны, то их определители также равны. Это свойство может быть использовано для проверки линейной независимости векторов или строк матрицы.
Использование свойств миноров позволяет упростить вычисления и решить множество задач в высшей математике.
Основные примеры использования миноров
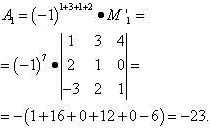
1. Вычисление определителя матрицы: миноры используются для вычисления определителя матрицы. Определитель матрицы может быть получен как сумма произведений элементов матрицы на соответствующие им миноры. Это позволяет нам анализировать свойства и характеристики матрицы.
2. Нахождение обратной матрицы: миноры также используются при нахождении обратной матрицы. Обратная матрица может быть получена путем нахождения алгебраических дополнений для каждого элемента матрицы и их транспонирования. Миноры играют роль в нахождении алгебраических дополнений.
3. Решение систем линейных уравнений: миноры могут быть использованы для решения систем линейных уравнений. С помощью миноров можно определить, является ли система совместной или несовместной, находить базисные переменные, а также выражать переменные через другие переменные, что упрощает решение системы.
4. Анализ многомерных данных: миноры могут быть использованы для анализа многомерных данных. Многомерные данные могут быть представлены в виде матрицы, где элементы матрицы представляют собой различные характеристики объектов. Миноры позволяют выделять подматрицы, содержащие наиболее важные характеристики и использовать их для анализа данных.
5. Оптимизация и оптимальное решение: миноры используются при оптимизации и нахождении оптимального решения. В задачах оптимизации миноры позволяют анализировать зависимости между переменными и определять, какие переменные влияют на результат задачи.
Это лишь несколько примеров использования миноров в высшей математике. Они являются мощным инструментом в анализе и решении различных задач, и их понимание и применение является важным для успешного изучения высшей математики.
Вопрос-ответ:
Что такое минор в высшей математике?
Минор в высшей математике — это определитель квадратной подматрицы матрицы, полученный удалением некоторых строк и столбцов.
Какие свойства имеют миноры в высшей математике?
Миноры в высшей математике обладают рядом свойств, таких как: свойство монотонности, свойство аддитивности, свойство мультипликативности и другие.
В каких областях применяются миноры в высшей математике?
Миноры в высшей математике находят широкое применение в различных областях, таких как линейная алгебра, теория вероятностей, дифференциальная геометрия, математическая физика и другие.
Какие задачи можно решать с помощью миноров в высшей математике?
С помощью миноров в высшей математике можно решать задачи нахождения обратной матрицы, ранга матрицы, определения линейной зависимости векторов, нахождения угла между векторами и другие.
Какую роль играют миноры в теории матриц?
Миноры играют важную роль в теории матриц, так как позволяют определить множество свойств матрицы, таких как ее ранг, определитель, обратимость и другие.


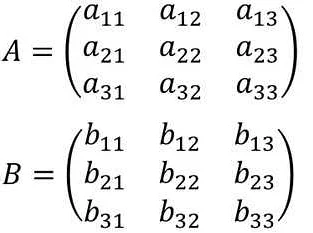
Минор высшая математика — это важное понятие, которое помогает решать сложные задачи и применять математические методы в различных областях науки и техники. Это математическое понятие используется в линейной алгебре и теории матриц для определения определителя матрицы. Минор высшая математика находит свое применение во многих областях, таких как физика, экономика, компьютерные науки и даже в биологии. Например, в физике миноры используются для нахождения собственных значений и собственных векторов матрицы, что позволяет решать задачи в квантовой механике и теории поля. В экономике они используются для анализа зависимостей между различными переменными, а в компьютерных науках — для разработки алгоритмов и оптимизации программ. Овладение минорами высшей математикой дает возможность решать сложные задачи и находить новые способы анализа данных. Это незаменимый инструмент для всех, кто интересуется наукой и стремится к развитию своих математических навыков. Поэтому, если вы хотите расширить свои знания и приобрести новые возможности, необходимо изучить этот важный аспект высшей математики.
Статья очень понятно и доступно описывает, что такое минор в высшей математике. Я всегда слышал этот термин, но никогда не понимал его значения и применение. Теперь стало ясно, что минор — это определитель квадратной подматрицы матрицы. А также, что миноры играют важную роль в линейной алгебре, теории графов и других областях математики. Теперь, благодаря этой статье, я лучше понимаю, как миноры используются для решения различных задач, таких как нахождение собственных значений матрицы или определение базиса пространства решений линейной системы уравнений. Я хотел бы еще больше узнать о применении миноров в практических задачах и о том, как они связаны с другими важными понятиями в математике. Спасибо за познавательную статью!
Эта статья очень интересна и полезна. Минор в высшей математике — это некоторый дополнительный определитель, который можно выделить из матрицы. Он имеет свои специфические свойства и играет важную роль в различных областях науки, таких как физика, экономика и компьютерная графика. Миноры используются для решения линейных систем уравнений, вычисления определителей матриц, нахождения собственных значений и векторов, а также для определения ранга и обратной матрицы. Они являются неотъемлемой частью линейной алгебры и находят применение во многих практических задачах. Чтение этой статьи помогло мне лучше понять, что такое миноры и как они применяются. Теперь я могу легче разбираться с математическими задачами и применять их знания в реальной жизни. Большое спасибо автору за доступное и понятное объяснение этой сложной темы. Рекомендую всем, кто интересуется математикой, ознакомиться с этой статьей.