Когда изучают матрицу по математике

Статья рассказывает о том, когда в школьной программе изучают матрицу по математике. Узнайте, какой класс и какие темы включают изучение этой важной математической концепции.

Матрица – это одна из фундаментальных концепций линейной алгебры, которую изучают в рамках математического образования. Она представляет собой таблицу чисел, расположенных в виде прямоугольной сетки. Изначально матрицы использовались для описания систем линейных уравнений, но с течением времени их применение стало шире: они используются в различных областях науки и техники, включая физику, экономику, информатику и другие.

Обучение матрицам начинается обычно в средней школе, когда ученики уже знакомы с основами алгебры и геометрии. На этом этапе изучаются основные понятия – размерность матрицы, элементы, операции с матрицами (сложение, вычитание, умножение), а также свойства этих операций. Учащиеся практикуются в решении простых задач, связанных с матрицами, и узнают, как применять их для решения систем линейных уравнений.

«Матрицы открывают перед нами мир новых математических возможностей. Они позволяют нам анализировать и описывать сложные явления, моделировать различные процессы и находить оптимальные решения», – говорит Алексей Петров, доцент кафедры математического анализа МГУ.

На старших классах глубже изучаются свойства матриц, их произведение, обратная матрица, детерминант и другие важные понятия. Ученикам предлагаются более сложные задачи, которые требуют творческого подхода и применения матриц в реальных ситуациях. Это помогает развить аналитическое мышление, умение работать с абстрактными объектами и находить логические решения.

Изучение матриц является важной частью математической подготовки и имеет большое практическое значение. Знание матриц помогает понять многие явления и процессы в нашей жизни, а также применять их для решения различных задач в науке и технике.

Определение матрицы

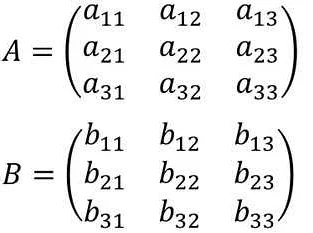
Матрицы используются в различных областях, включая линейную алгебру, теорию вероятностей, статистику, компьютерную графику и т.д. Они позволяют структурировать и хранить информацию, а также выполнять различные операции над этой информацией.

Матрицу обычно обозначают заглавной латинской буквой, например, A, B, C и т.д. Размерность матрицы определяется количеством строк и столбцов, и обозначается в виде m x n, где m — количество строк, а n — количество столбцов.

Элементы матрицы могут быть различных типов, например, действительные числа, комплексные числа, булевы значения и т.д. Матрицы могут быть квадратными (когда количество строк равно количеству столбцов) или прямоугольными (когда количество строк не равно количеству столбцов).

Матрицы можно складывать, вычитать, умножать на число, умножать друг на друга, транспонировать и выполнять другие операции. Некоторые из основных понятий, связанных с матрицами, включают определитель, ранг, обратную матрицу, собственные значения и векторы.

Пример:

Рассмотрим матрицу A:

A = \(\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}\)

Эта матрица имеет 2 строки и 3 столбца, поэтому ее размерность равна 2 x 3. Ее элементы обозначаются через индексы, например, \(a_{11}\) — элемент в первой строке и первом столбце, равный 1, \(a_{23}\) — элемент во второй строке и третьем столбце, равный 6.

Основные операции с матрицами

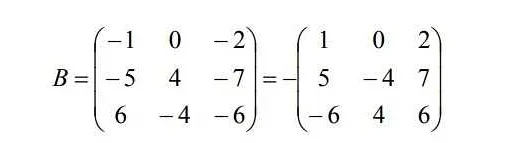
Основные операции с матрицами включают:

ОперацияОписание

Сложение	Для сложения двух матриц необходимо сложить соответствующие элементы этих матриц. Сложение возможно только для матриц одинакового размера.
Вычитание	Для вычитания одной матрицы из другой необходимо вычесть соответствующие элементы этих матриц. Вычитание возможно только для матриц одинакового размера.
Умножение на число	Для умножения матрицы на число необходимо умножить каждый элемент матрицы на это число.
Умножение матриц	Для умножения двух матриц необходимо умножить соответствующие элементы строк первой матрицы на соответствующие элементы столбцов второй матрицы и сложить полученные произведения.
Транспонирование	Для транспонирования матрицы необходимо поменять строки и столбцы матрицы местами.
Определитель	Определитель матрицы — это число, которое можно вычислить для квадратной матрицы. Определитель позволяет определить, обратима ли матрица.

Знание основных операций с матрицами позволяет решать различные математические и технические задачи, а также применять матрицы в компьютерной графике, статистике, физике и других областях науки.

Системы линейных уравнений и матрицы

Система линейных уравнений состоит из нескольких уравнений, каждое из которых представляет собой линейное уравнение. Линейное уравнение имеет вид:

a1x1 + a2x2 + … + anxn = b

где a1, a2, …, an — коэффициенты, x1, x2, …, xn — неизвестные переменные, b — свободный член.

Систему линейных уравнений можно записать в матричной форме, используя матрицы. Матрица системы состоит из коэффициентов при неизвестных и свободных членов. Например, система из двух уравнений с двумя неизвестными может быть записана как:

a11	a12	|	b1
a21	a22	|	b2

где a11, a12, a21, a22 — коэффициенты, b1, b2 — свободные члены.

С помощью матриц можно решать системы линейных уравнений, используя методы элементарных преобразований. Эти методы позволяют привести матрицу системы к ступенчатому виду или к диагональному виду, что позволяет найти решение системы или определить, что система несовместна.

Виды матриц

В математике существует несколько видов матриц, которые имеют свои особенности и применяются в различных областях.

• Квадратная матрица: это матрица, у которой число строк равно числу столбцов. Квадратные матрицы широко используются в линейной алгебре и теории вероятностей.
• Прямоугольная матрица: это матрица, у которой число строк не равно числу столбцов. Прямоугольные матрицы могут быть использованы, например, для представления данных в таблицах и базах данных.
• Диагональная матрица: это квадратная матрица, у которой все элементы вне главной диагонали равны нулю. Диагональные матрицы широко применяются в физике и инженерии для описания линейных систем.
• Единичная матрица: это квадратная матрица, у которой все элементы на главной диагонали равны единице, а все остальные элементы равны нулю. Единичные матрицы используются в линейной алгебре и теории вероятностей.
• Нулевая матрица: это матрица, у которой все элементы равны нулю. Нулевые матрицы могут быть использованы, например, для инициализации переменных в компьютерных программах.

Это только некоторые из видов матриц, которые изучаются в математике. Каждый вид матрицы имеет свои свойства и применения, и их изучение позволяет более глубоко понять структуру и связи между данными.

Матрицы и линейные преобразования

Линейные преобразования представляют собой математические операции, которые изменяют исходные векторы или матрицы. Они описывают линейные зависимости и отношения между объектами. Примеры линейных преобразований включают вращение, масштабирование, сдвиг и отражение.

Матрицы позволяют компактно представлять линейные преобразования и удобно выполнять операции с векторами и матрицами. Они состоят из чисел, расположенных в виде прямоугольной таблицы. Каждое число в матрице называется элементом, а его положение определяется номерами строки и столбца.

Матрицы можно умножать, складывать, находить определитель и обратную матрицу. Умножение матриц позволяет комбинировать линейные преобразования, а сложение матриц соответствует комбинированию результатов преобразований. Определитель матрицы позволяет определить, является ли линейное преобразование обратимым. Обратная матрица позволяет выполнить обратное преобразование.

Матрицы и линейные преобразования широко применяются в графике и компьютерной графике, физике, экономике и других областях. Они помогают моделировать и анализировать различные явления и процессы, а также решать задачи оптимизации и управления.

Изучение матриц и линейных преобразований позволяет развить абстрактное мышление, улучшить навыки анализа и решения задач, а также освоить базовые инструменты алгебры и линейной алгебры.

Собственные значения и собственные векторы матрицы

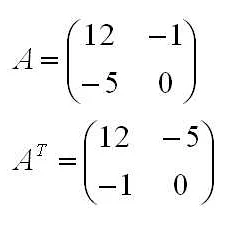
Собственные значения матрицы являются корнями характеристического уравнения, которое определяется как определитель разности матрицы и единичной матрицы, умноженный на неизвестную λ.

Собственные векторы матрицы – это такие векторы, которые при умножении на матрицу остаются коллинеарными с исходным вектором. Другими словами, они не меняют свое направление, только изменяются по длине в λ раз.

Собственные значения и собственные векторы матрицы могут иметь важное физическое или геометрическое значение. Например, при решении задач на полях физики собственные значения матрицы могут представлять энергетические уровни, а собственные векторы – состояния системы.

Собственные значенияСобственные векторы

Определяются как корни характеристического уравнения	Остаются коллинеарными с исходным вектором при умножении на матрицу
Могут иметь физическое или геометрическое значение	Могут иметь физическое или геометрическое значение

Вопрос-ответ:

Какие этапы обучения матрицам существуют?

Обучение матрицам проходит в несколько этапов: введение в понятие матрицы, основные операции с матрицами, решение систем линейных уравнений с помощью матриц, нахождение определителя и обратной матрицы, применение матриц в различных областях науки и техники.

Каковы основные концепции, связанные с изучением матриц?

Основные концепции, связанные с изучением матриц, включают в себя понятие размерности матрицы, элементы матрицы, операции с матрицами (сложение, умножение), свойства матриц (коммутативность, ассоциативность, дистрибутивность), системы линейных уравнений, определитель матрицы, обратная матрица и применение матриц в различных областях.

Каковы основные этапы введения в понятие матрицы?

Основные этапы введения в понятие матрицы включают в себя знакомство с определением и обозначением матрицы, различными типами матриц (квадратная, прямоугольная, нулевая), понятием размерности матрицы, элементами матрицы и их расположением в матрице.

Какие операции с матрицами необходимо изучить?

Необходимо изучить операции сложения и умножения матриц, а также умножение матрицы на число. Операция сложения матриц выполняется покомпонентно, то есть каждый элемент результирующей матрицы равен сумме соответствующих элементов слагаемых матриц. Операция умножения матриц выполняется путем перемножения строк первой матрицы на столбцы второй матрицы.

Как применяются матрицы в различных областях науки и техники?

Матрицы широко применяются в различных областях науки и техники. Например, они используются для решения систем линейных уравнений, моделирования физических процессов, обработки изображений и звука, компьютерной графики, криптографии, анализа данных и многих других. Матрицы являются мощным и удобным инструментом для работы с большими объемами данных и сложными математическими моделями.

Что такое матрица?

Матрица — это математический объект, представляющий собой прямоугольную таблицу чисел или символов, разделенных на строки и столбцы. Она является одним из базовых понятий линейной алгебры и широко применяется в различных областях науки и техники.

Какие этапы обучения матрицам существуют?

Обучение матрицам обычно проходит в несколько этапов. На начальном этапе изучаются основные понятия, такие как размерность матрицы, операции с матрицами (сложение, умножение и т. д.), а также свойства матриц. Затем переходят к более сложным темам, таким как нахождение определителя матрицы, решение систем линейных уравнений с помощью матриц и другие приложения матриц в линейной алгебре. В конечном итоге, обучение матрицам может продолжаться и в углубленных курсах по линейной алгебре и прикладной математике.

Практическое применение матриц в реальной жизни

В физике матрицы применяются для описания взаимодействия множества физических величин. Например, при моделировании электрических цепей, матрицы используются для представления системы уравнений, описывающих токи и напряжения в цепи.

В экономике матрицы используются для анализа и прогнозирования экономических данных. Они могут быть использованы для моделирования потоков товаров и услуг, распределения ресурсов и управления финансовыми портфелями.

В компьютерной графике матрицы широко используются для трансформации исходных изображений. Они позволяют выполнять такие операции, как масштабирование, поворот и смещение изображений.

В технических науках матрицы применяются для моделирования и анализа систем. Например, они могут быть использованы для описания и управления движением роботов или для анализа данных в области машинного обучения.

Понимание и применение матриц в реальной жизни является важным навыком, который может быть полезен во многих областях деятельности. Они позволяют эффективно моделировать и анализировать сложные системы, а также решать задачи с использованием компьютерных технологий.

Видео по теме: