Что такое минор в математике

Минор в математике — это определитель квадратной подматрицы, полученной из исходной матрицы путем вычеркивания некоторых строк и столбцов. Миноры широко используются при решении систем линейных уравнений, нахождении обратной матрицы, определении собственных значений и в других математических задачах.

Минор – это одно из ключевых понятий в линейной алгебре и матричном анализе. В математике минор определяется как определитель квадратной подматрицы исходной матрицы.

Миноры играют важную роль в различных областях математики и науки. Они широко применяются в линейной алгебре, теории графов, статистике, физике, экономике и других дисциплинах. Миноры позволяют анализировать и изучать различные свойства и характеристики матриц и систем линейных уравнений.

Применение миноров в математике очень разнообразно. С их помощью можно вычислять ранг матрицы, находить собственные значения, решать системы линейных уравнений, определять обратимость матрицы и многое другое.

Изучение миноров позволяет получить глубокое понимание структуры и свойств матриц, а также решать разнообразные задачи в науке и технике. Знание миноров является важным инструментом для успешного применения математики в практических задачах.

Что такое минор в математике

Для того чтобы вычислить минор, необходимо выбрать определенные строки и столбцы матрицы и удалить их из исходной матрицы. Затем оставшиеся элементы матрицы образуют новую матрицу, из которой можно вычислить минор.

Миноры широко применяются в различных областях математики и физики. Они используются для вычисления определителей, решения систем линейных уравнений, нахождения собственных значений и векторов, а также в теории графов и комбинаторике.

Миноры имеют важное практическое значение, поскольку они позволяют анализировать свойства и характеристики матрицы и решать различные задачи, связанные с линейной алгеброй и теорией определителей.

Важно отметить, что миноры могут быть положительными, отрицательными или нулевыми в зависимости от свойств исходной матрицы. Изучение миноров помогает понять структуру и свойства матрицы, а также найти ее важные характеристики.

Определение и свойства миноров

Основные свойства миноров:

1. Минор может быть вычислен только для квадратных матриц.
2. Минор зависит от выбранных строк и столбцов исходной матрицы.
3. Если в исходной матрице поменять местами строки или столбцы, то минор не изменится.
4. Если одна из строк или столбцов исходной матрицы состоит из нулей, то минор будет равен нулю.
5. Если одна строка или столбец исходной матрицы пропорциональна другой строке или столбцу, то минор будет равен нулю.

Миноры имеют важное значение в линейной алгебре и матричных вычислениях. Они используются для решения систем линейных уравнений, нахождения обратной матрицы, определения ранга матрицы и многих других задач.

Миноры в теории матриц

Миноры определяются как определители подматриц. Подматрица — это матрица, полученная из исходной матрицы путем выбора нескольких строк и столбцов. Минор матрицы получается путем вычисления определителя этой подматрицы.

Важно отметить, что миноры характеризуют свойства матрицы и могут быть использованы для определения ее ранга, линейной независимости строк и столбцов, проверки совместности системы линейных уравнений и других задач. Кроме того, миноры позволяют упростить вычисления и облегчить решение сложных математических задач.

Одним из важных применений миноров является нахождение обратной матрицы. Используя миноры, можно проверить обратимость матрицы и вычислить обратную матрицу, что позволяет решать системы линейных уравнений и другие задачи. Миноры также применяются для нахождения определителя матрицы, который отражает свойства и характеристики матрицы.

Таким образом, миноры играют важную роль в теории матриц и имеют широкое применение в различных областях математики. Изучение и использование миноров позволяет более глубоко понять и анализировать свойства матриц, решать сложные задачи и сделать выводы о характеристиках системы линейных уравнений.

Применение миноров в линейной алгебре

Одним из основных применений миноров является нахождение определителя матрицы. Определитель матрицы можно выразить через миноры, используя формулу Лапласа. Для этого матрица разбивается на подматрицы, миноры которых затем вычисляются и суммируются с определенными знаками. Таким образом, миноры позволяют найти точное значение определителя матрицы.

Еще одним важным применением миноров является решение систем линейных уравнений. Если матрица системы имеет ненулевой определитель, то система имеет единственное решение. Миноры позволяют проверить, является ли определитель ненулевым, и таким образом определить, имеет ли система линейных уравнений решение.

Миноры также используются для нахождения ранга матрицы. Ранг матрицы определяется как максимальное количество линейно независимых строк или столбцов. Миноры помогают определить, какие строки или столбцы являются линейно независимыми, и таким образом вычислить ранг матрицы.

Кроме того, миноры используются для проверки линейной зависимости векторов. Если минор некоторой матрицы равен нулю, то векторы, соответствующие этим строкам или столбцам, являются линейно зависимыми. Таким образом, миноры позволяют определить, является ли система векторов линейно зависимой или линейно независимой.

Таким образом, миноры играют важную роль в линейной алгебре и находят применение в различных областях математики.

Миноры в теории графов

Миноры графа могут быть использованы для анализа структуры и свойств исходного графа. Они позволяют изучать подграфы и выявлять взаимосвязи и зависимости между вершинами и ребрами.

Миноры также позволяют классифицировать графы и определить их свойства. Например, минор графа может иметь меньшую плотность, быть деревом или содержать циклы определенной длины.

Использование миноров в теории графов позволяет решать различные задачи, такие как поиск оптимальных путей, определение связности графа, выявление гамильтоновых циклов и многое другое.

Таким образом, миноры в теории графов являются мощным инструментом для анализа и изучения различных свойств и характеристик графов.

Связь миноров с определителями

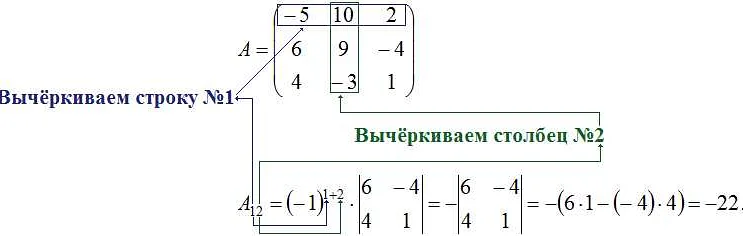
Минор матрицы получается путем вычеркивания определенных строк и столбцов из исходной матрицы. К примеру, если матрица имеет размерность 3×3, то минору будет соответствовать матрица размерностью 2×2, полученная после вычеркивания определенной строки и столбца.

Связь миноров с определителями заключается в том, что определитель матрицы можно выразить через миноры. Существуют различные формулы и методы, позволяющие вычислить определитель матрицы с использованием миноров.

Например, для матрицы размерностью 3×3 определитель можно выразить следующим образом:

| a b c |

| d e f | = a(ei − fh) − b(di − fg) + c(dh − eg)

| g h i |

В данной формуле входят миноры 2×2, которые образуются из исходной матрицы путем вычеркивания определенных строк и столбцов.

Таким образом, миноры играют важную роль в вычислении определителей матриц и позволяют упростить процесс расчета. Знание связи миноров с определителями является необходимым для понимания и применения математических методов и формул.

Расширение понятия минора

Однако, понятие минора может быть расширено и применено не только для квадратных матриц, но и для прямоугольных матриц. В случае прямоугольной матрицы, минор — это определитель квадратной подматрицы, полученной из исходной матрицы путем выбора определенных строк и столбцов.

Расширение понятия минора позволяет более гибко использовать его в различных математических исследованиях и приложениях. Например, миноры прямоугольной матрицы могут быть использованы для анализа зависимости между различными переменными в системе уравнений, или для описания свойств и структуры графов.

Таким образом, расширение понятия минора дает возможность более глубокого и всестороннего анализа различных математических объектов и систем, позволяет выявить закономерности и связи, которые могут быть полезны в различных прикладных областях.

МатрицаМиноры

1 2 3 4 5 6 7 8 9

Минор 1Минор 2Минор 3 1 2 3 4 5 6

Вычисление миноров

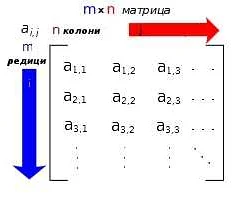
Обозначим исходную матрицу размером n × n как A. Для вычисления минора Mi,j выбираются i строка и j столбец, и из матрицы A удаляются эти строки и столбцы. Полученная матрица называется подматрицей и обозначается как Ai,j. Минор Mi,j равен определителю подматрицы Ai,j.

Вычисление минора можно выполнить с помощью разложения по определенной строке или столбцу. Разложение по строке позволяет выразить минор через миноры меньшего порядка. Аналогично, разложение по столбцу позволяет выразить минор через миноры меньшего порядка.

Вычисление миноров может быть полезно в различных областях математики, таких как теория вероятностей, линейная алгебра, теория дифференциальных уравнений и др. Миноры могут быть использованы для решения систем линейных уравнений, определения обратной матрицы, нахождения собственных значений и векторов матрицы и других задач.

Матрица A	Матрица Ai,j	Минор Mi,j
a11 a12 a13	a21 a22 a23	a31 a32 a33	a41 a42 a43	a51 a52 a53	a61 a62 a63	a71 a72 a73	a81 a82 a83
a11 a12 a13	a21 a22 a23	a31 a32 a33	a41 a42 a43	a51 a52 a53	a61 a62 a63	a71 a72 a73	a81 a82 a83

Примеры использования миноров в реальных задачах

1. Определение вырожденности матрицы. Миноры позволяют определить, является ли матрица вырожденной, то есть имеет нулевой определитель. Если хотя бы один из миноров матрицы равен нулю, то матрица является вырожденной.
2. Нахождение ранга матрицы. Ранг матрицы можно определить с помощью миноров. Для этого необходимо последовательно вычислить все ненулевые миноры матрицы и найти максимальный порядок минора, который не равен нулю. Ранг матрицы равен порядку найденного минора.
3. Решение систем линейных уравнений. Миноры позволяют выяснить, имеет ли система линейных уравнений единственное решение или не имеет решений вообще. Если все миноры матрицы системы ненулевые, то система имеет единственное решение. В противном случае система может иметь бесконечное количество решений или не иметь их вовсе.
4. Нахождение обратной матрицы. Миноры используются в процессе вычисления обратной матрицы. Если все миноры матрицы ненулевые, то матрица имеет обратную, и ее можно найти с помощью формулы, которая зависит от миноров исходной матрицы.
5. Определение линейной независимости векторов. Миноры позволяют определить, являются ли векторы линейно независимыми. Если все миноры из столбцов векторов ненулевые, то векторы являются линейно независимыми. В противном случае они линейно зависимы.

Это лишь некоторые примеры использования миноров в математике. Миноры имеют широкое применение в различных областях, таких как физика, экономика, компьютерная графика и другие, где требуется анализ матриц и систем линейных уравнений.

Видео по теме:

Что такое минор в математике?

Минор в математике — это определитель квадратной подматрицы матрицы. Он вычисляется путем выбора i строк и j столбцов из исходной матрицы и расчета определителя полученной подматрицы.

Какие применения миноров в математике?

Миноры широко используются в линейной алгебре и теории матриц. Они позволяют решать уравнения, находить обратные матрицы, находить ранг матрицы и многое другое. Также миноры применяются в анализе и оптимизации, например, в задачах определения оптимальной конфигурации системы.

Как вычислять миноры матрицы?

Для вычисления миноров матрицы необходимо выбрать i строк и j столбцов из исходной матрицы и вычислить определитель полученной подматрицы. Определитель можно вычислить путем разложения по любой строке или столбцу или с помощью специальных методов, таких как метод Гаусса или метод Крамера.

Что такое минор в математике?

Минор — это определитель квадратной подматрицы матрицы. В математике миноры используются для решения систем линейных уравнений, вычисления обратной матрицы, нахождения собственных значений и векторов, а также для решения задач оптимизации.