Что такое вершина в математике

Вершина в математике — это точка, которая является конечной или начальной точкой ребра или отрезка. Вершины играют важную роль в графах, треугольниках, многогранниках и других геометрических фигурах. Вершины имеют координаты и могут быть объединены с другими вершинами для создания графов и моделей. Вершины также могут быть использованы для определения путей и расстояний в графе. Понимание понятия вершины является важным основным принципом в математике и науке.

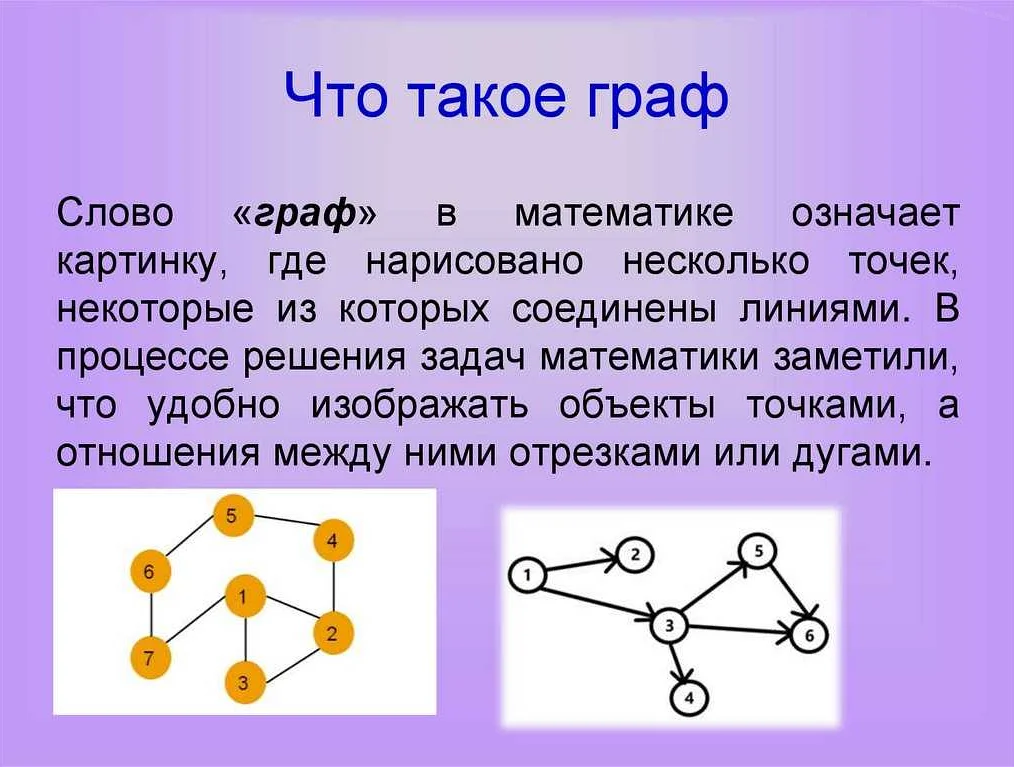
Вершина – это одна из основных понятий в математике, которое широко используется в различных областях этой науки. Обычно вершина определяется как точка, в которой сходятся ребра или грани графа или многогранника. Вершины могут быть двухмерными (как в случае с графами) или трехмерными (как в случае с многогранниками).

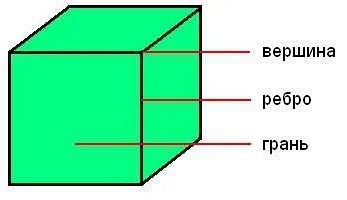
Вершины имеют ряд свойств, которые делают их особенными. Одно из главных свойств вершин – это их количество. Количество вершин в графе или многограннике может быть разным и зависит от его структуры. Например, в треугольнике есть три вершины, в кубе – восемь вершин, а в пятиугольнике – пять вершин.

Вершины играют важную роль в различных математических задачах и конструкциях. Они могут быть использованы для определения путей и связей между объектами, для анализа структуры и свойств объектов, а также для решения задач оптимизации и поиска минимума или максимума функций.

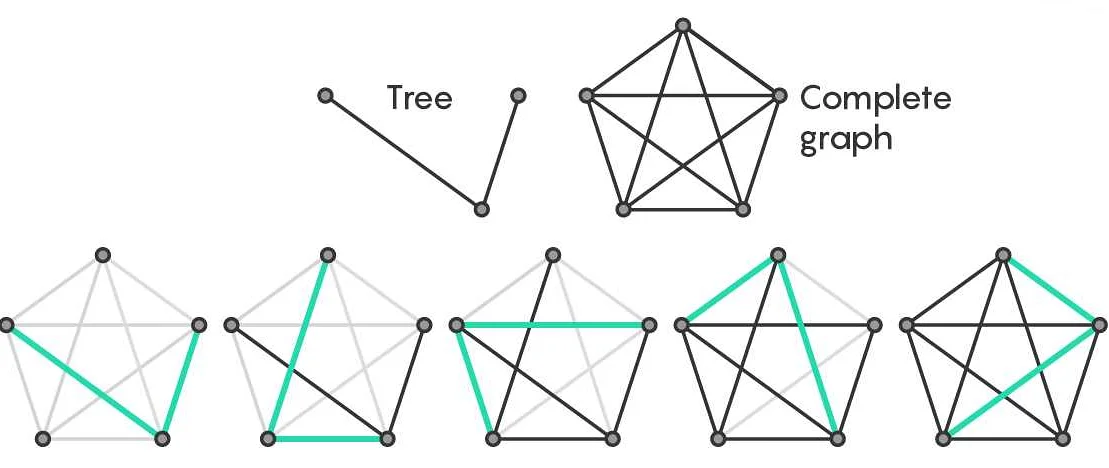
Примером использования вершин в математике являются деревья. В дереве каждая вершина может иметь несколько дочерних вершин. Это позволяет организовать иерархическую структуру данных и эффективно хранить информацию.

Определение вершины

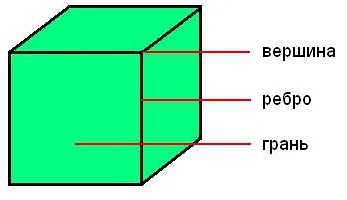
Вершины играют важную роль в различных областях математики. В графовой теории, вершины представляют объекты или события, а ребра представляют отношения или связи между ними. В геометрии, вершины определяют форму и структуру объектов. В алгебре, вершины могут быть точками экстремума функций. Вершины также используются в теории игр, теории чисел и других областях математики.

Примеры вершин:

ГрафГеометрия

Свойства вершины

Вершина имеет следующие свойства:

1. Степень вершины. Степень вершины определяется как количество ребер, инцидентных данной вершине. Например, вершина с двумя инцидентными ребрами имеет степень 2. Степень вершины может быть как нулевой, так и положительной.
2. Смежные вершины. Смежные вершины — это вершины, соединенные ребром с данной вершиной. Например, если вершина A соединена ребром с вершиной B, то вершина B считается смежной с вершиной A.
3. Изолированная вершина. Изолированная вершина — это вершина, у которой степень равна нулю. Такая вершина не имеет смежных вершин и не связана ни с одной другой вершиной.

Вершины используются для описания и анализа различных структур и сетей, таких как социальные сети, дорожные сети, электрические схемы и многие другие.

Примеры вершин

1. Вершина в треугольнике: в треугольнике каждая из трёх точек, где пересекаются его стороны, является вершиной.
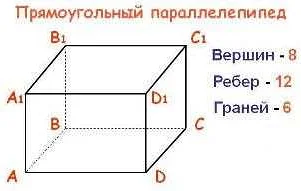
2. Вершина в кубе: в кубе каждая из восьми точек, где пересекаются его рёбра, является вершиной.
3. Вершина в графе: в ориентированном или неориентированном графе вершинами могут быть различные объекты, например, города на карте или узлы в сети.

Это лишь некоторые примеры вершин, которые могут встретиться в различных математических объектах. Вершины являются важными понятиями в математике и используются для анализа и описания различных структур и связей между объектами.

Вершина в графе

Каждая вершина в графе имеет свои свойства и характеристики:

• Степень вершины — это количество ребер, которые выходят из данной вершины. Например, вершина с тремя ребрами имеет степень 3.
• Соседние вершины — это вершины, которые имеют общее ребро с данной вершиной.

Вершины в графе могут быть направленными или ненаправленными:

• В ненаправленном графе ребра между вершинами не имеют направления. Например, если вершины А и Б соединены ребром, то можно перемещаться между ними в обоих направлениях.
• В направленном графе ребра имеют направление. Например, если вершина А соединена с вершиной Б направленным ребром, то можно перемещаться только от вершины А к вершине Б.

Примеры использования вершин в графе:

• В социальных сетях вершины могут представлять пользователей, а ребра — связи между ними.
• В дорожных сетях вершины могут представлять города, а ребра — дороги между ними.
• В компьютерных сетях вершины могут представлять компьютеры, а ребра — соединения между ними.

Вершина в геометрии

В геометрии вершина может иметь несколько различных значений в зависимости от контекста. В общем смысле, вершиной называется точка, в которой встречаются две или более линии, отрезка или грани.

В трехмерной геометрии, вершины могут быть частью полиэдра, которые представляют собой многогранники, имеющие плоские грани и ребра. В этом контексте, вершина определяется как точка пересечения трех или более ребер или граней полиэдра.

Например, в кубе есть 8 вершин, так как каждый угол куба является вершиной. В пространстве, вершина может быть точкой, где пересекаются три плоскости или три отрезка.

Вершины также играют важную роль в графической геометрии, где они определяют форму и структуру фигуры. Например, в треугольнике вершины являются концами его трех сторон и определяют его форму и углы.

Таким образом, вершина в геометрии является важным понятием, определяющим точку пересечения линий, отрезков или граней, и используется для определения формы и структуры геометрических фигур.

Вершина в теории игр

В теории игр вершиной называется комбинация стратегий, выбранных всеми игроками в определенной игре. Вершина представляет собой точку в стратегическом пространстве игры, где каждый игрок принимает определенное решение, основываясь на своей стратегии и стратегиях других игроков.

Вершины в теории игр могут быть разных типов. Например, в кооперативной игре, где игроки сотрудничают друг с другом, вершина представляет собой комбинацию стратегий, которые приводят к определенному исходу игры для всех игроков. В некооперативной игре, где игроки действуют независимо друг от друга, каждая вершина представляет собой комбинацию стратегий, которые определяют исход игры для каждого игрока.

Вершины в теории игр имеют свойства, которые могут быть использованы для анализа игры. Например, равновесие Нэша — это вершина игры, где ни одному игроку не выгодно изменить свою стратегию, при условии, что стратегии других игроков остаются неизменными. Равновесие Нэша является одной из ключевых концепций в теории игр и имеет множество применений в экономике, политике и других областях.

Примером вершины в теории игр может быть ситуация, когда два игрока играют игру «Камень, ножницы, бумага». Вершиной будет комбинация стратегий, выбранных обоими игроками. Например, если один игрок выбрал «камень», а другой игрок выбрал «бумагу», то это будет вершина игры, в которой один игрок выиграет, а другой проиграет.

Вершина в оптимизации

Вершина в оптимизации может быть найдена с помощью различных методов, включая метод градиентного спуска, метод Ньютона-Рафсона и метод симплекса. Эти методы позволяют исследовать пространство решений, чтобы найти оптимальные значения переменных и достичь наилучшего результата.

ПримерОписание

Задача коммивояжера	Вершина в этой задаче представляет собой оптимальный маршрут, который проходит через все города и возвращается в исходный город, минимизируя общее расстояние.
Модель маркетинговых решений	Вершина в этой модели представляет оптимальный набор маркетинговых решений, который максимизирует прибыль компании при ограниченных ресурсах.

Изучение вершин в оптимизации позволяет найти наилучшие решения и оптимизировать процессы в различных областях, таких как логистика, производство, финансы и маркетинг.

Вершина в алгоритмах

Вершины в алгоритмах имеют следующие свойства:

СвойствоОписание

Степень	Степень вершины — это количество ребер, смежных с данной вершиной. Она может быть исходящей (количество ребер, исходящих из вершины) или входящей (количество ребер, входящих в вершину).
Соседи	Соседи вершины — это другие вершины, с которыми эта вершина соединена ребрами. В алгоритмах это очень важная информация, так как она позволяет найти пути между вершинами или выполнить другие операции.
Метки	Метки или атрибуты могут быть присвоены вершинам и использоваться для хранения дополнительной информации о вершинах. Например, в алгоритмах поиска в ширину или в глубину метки могут использоваться для отслеживания пройденных вершин.

Примеры использования вершин в алгоритмах:

1. Алгоритм Дейкстры использует вершины для поиска кратчайшего пути в графе. Каждая вершина имеет метку, которая обозначает текущее минимальное расстояние от начальной вершины до данной вершины.

2. Алгоритм Краскала использует вершины для построения минимального остовного дерева в связном графе. Каждая вершина представляет отдельное поддерево, которое со временем объединяется с другими поддеревьями.

Таким образом, вершины в алгоритмах играют важную роль и позволяют представить и оперировать сущностями в графах и других структурах данных.

Видео по теме:

Что такое вершина в математике?

В математике вершина – это точка, которая является концом отрезка или луча. Она также может быть точкой пересечения нескольких отрезков или лучей.

Какую роль играют вершины в графах?

Вершины в графах играют ключевую роль. Они являются узлами, в которых сходятся ребра и от которых исходят новые ребра. Вершины графа могут представлять объекты или события, а ребра – их взаимосвязь или отношение. Вершины графа позволяют анализировать и моделировать сложные системы, такие как социальные сети, транспортные сети и т. д.