Что такое множество дискретная математика

Множество в дискретной математике — это совокупность различных элементов, неупорядоченная коллекция объектов. Узнайте, как множества используются для решения задач в дискретной математике и какие основные операции можно выполнять над множествами.

Множество — одно из основных понятий дискретной математики. Оно представляет собой совокупность различных элементов, которые называются членами множества. В отличие от числовых систем, множество может содержать любые объекты: числа, буквы, слова, предметы и т.д. Важно отметить, что каждый элемент может входить в множество только один раз.

Множество обычно обозначается заглавной буквой, а его элементы записываются в фигурных скобках через запятую. Например, множество натуральных чисел можно записать так: {1, 2, 3, 4, …}. Если элементы множества обладают каким-то общим свойством, то можно использовать формулу для их описания. Например, множество всех четных чисел можно записать как {x | x является четным числом}.

Примеры множеств:

• Множество гласных букв русского алфавита: {а, е, ё, и, о, у, ы, э, ю, я}
• Множество простых чисел: {2, 3, 5, 7, 11, …}
• Множество цветов радуги: {красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый}

Множества играют важную роль в дискретной математике и используются для описания различных явлений и отношений. Они являются основой для других понятий, таких как операции над множествами, подмножества, объединение и пересечение множеств. Поэтому понимание основных свойств и определений множеств является необходимым для изучения дискретной математики.

Определение множества и его элементов

Множество обычно обозначается заглавными буквами латинского алфавита, например A, B, C. Элементы множества обычно записываются в фигурных скобках, разделенные запятыми. Например, множество A может содержать элементы {1, 2, 3}, а множество B может содержать элементы {a, b, c}.

Элемент множества — это каждый отдельный объект, который принадлежит данному множеству. Например, если множество A содержит элементы {1, 2, 3}, то каждое из чисел 1, 2 и 3 является элементом множества A.

Важно отметить, что множество не может содержать повторяющиеся элементы, поскольку каждый элемент должен быть уникальным. Если повторяющиеся элементы все же присутствуют, то они считаются одним и тем же элементом.

Видео по теме:

Операции над множествами

Множества в дискретной математике поддерживают несколько базовых операций, которые позволяют выполнять различные операции с элементами множеств.

Основные операции над множествами включают:

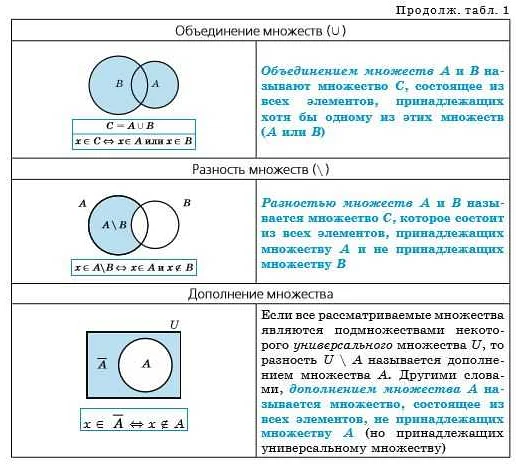
• Объединение: данная операция позволяет объединить два или более множества в одно, включая все элементы из исходных множеств. Обозначается символом «∪».
• Пересечение: данная операция позволяет найти все элементы, которые есть одновременно в двух или более множествах. Обозначается символом «∩».
• Разность: данная операция позволяет найти все элементы, которые принадлежат одному множеству, но не принадлежат другому. Обозначается символом «\» или «-«.
• Дополнение: данная операция позволяет найти все элементы, которые не принадлежат заданному множеству. Обозначается символом «¬» или «C».

Например, если у нас есть два множества:

• А = {1, 2, 3}
• B = {3, 4, 5}

Тогда:

• Объединение A и B будет равно A ∪ B = {1, 2, 3, 4, 5}
• Пересечение A и B будет равно A ∩ B = {3}
• Разность A и B будет равна A \ B = {1, 2}
• Дополнение A будет равно ¬A = {4, 5}

Таким образом, операции над множествами позволяют находить общие элементы, различия и другую полезную информацию, которая может быть полезна при анализе данных или решении задач дискретной математики.

Пустое множество и универсальное множество

Пустое множество, также известное как нулевое множество или множество без элементов, обозначается символом ∅ или {} и не содержит ни одного элемента. Математически можно записать его так: ∅ = {}.

Универсальное множество, также известное как множество всех элементов или множество всех возможных значений, обозначается символом U. Оно содержит все элементы, которые рассматриваются в данной области. Например, если мы рассматриваем множество натуральных чисел, то универсальным множеством будет множество всех натуральных чисел. Математически можно записать его так: U = {0, 1, 2, 3, …}.

Пустое множество является подмножеством любого другого множества, так как не содержит элементов. Универсальное множество, напротив, содержит все возможные элементы, поэтому является надмножеством любого другого множества.

Понимание пустого и универсального множества играет важную роль в дискретной математике и используется при определении операций над множествами, таких как объединение, пересечение и разность.

Примеры множеств в дискретной математике

Множество натуральных чисел:

Н={1, 2, 3, 4, 5, …}

Множество четных чисел:

Ч={2, 4, 6, 8, …}

Множество нечетных чисел:

НЧ={1, 3, 5, 7, …}

Множество простых чисел:

П={2, 3, 5, 7, 11, …}

Множество цветов радуги:

Ц={красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый}

Множество букв латинского алфавита:

А={A, B, C, D, …, Z}

Множество дней недели:

Д={Понедельник, Вторник, Среда, Четверг, Пятница, Суббота, Воскресенье}

Подмножество и надмножество

В дискретной математике множество может содержать другие множества. В этом случае говорят о подмножестве и надмножестве.

Подмножество — это множество, элементы которого являются также элементами другого множества. Иными словами, если каждый элемент подмножества принадлежит некоторому множеству, то говорят, что это множество является подмножеством. Подмножество обозначается символом ⊆.

Например, пусть есть множество A = {1, 2, 3} и множество B = {1, 2, 3, 4, 5}. Тогда множество A является подмножеством множества B, так как каждый элемент множества A также является элементом множества B.

Надмножество — это множество, в которое входят все элементы другого множества. Другими словами, если каждый элемент некоторого множества является также элементом надмножества, то говорят, что это множество является надмножеством. Надмножество обозначается символом ⊇.

Продолжая пример с множествами A и B, можно сказать, что множество B является надмножеством множества A, так как все элементы множества A также являются элементами множества B.

Иногда множество может быть одновременно и подмножеством, и надмножеством другого множества. Например, если есть множество C = {1, 2, 3}, то оно является и подмножеством множества A и надмножеством множества B.

Важно отметить, что пустое множество является подмножеством любого множества, а любое множество является надмножеством пустого множества.

Равенство и неравенство множеств

Для проверки равенства множеств необходимо сравнить их элементы. Если все элементы одного множества присутствуют в другом множестве, и наоборот, то они считаются равными.

Неравенство множеств означает, что они содержат различные элементы или могут иметь разное количество элементов. Например, множество C = {1, 2, 3} не равно множеству D = {4, 5, 6}, так как они содержат разные элементы.

Для доказательства неравенства множеств необходимо найти хотя бы один элемент, который присутствует в одном множестве и отсутствует в другом множестве.

Вопрос-ответ:

Что такое множество в дискретной математике?

Множество в дискретной математике — это совокупность элементов, которые могут быть любого типа и не повторяться.

Каким образом определяется множество?

Множество определяется перечислением его элементов в фигурных скобках, разделенных запятыми. Например, {1, 2, 3} — множество из трех элементов.

Какие примеры множеств можно привести?

Примерами множеств могут быть множество натуральных чисел {1, 2, 3, …}, множество четных чисел {2, 4, 6, …}, множество гласных букв {а, е, и, о, у, э, ю, я}, и множество цветов радуги {красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый}.

Можно ли множество пустым?

Да, можно определить пустое множество, которое не содержит ни одного элемента. Оно обозначается фигурными скобками без элементов: {}.

Что такое подмножество?

Подмножество — это множество, элементы которого являются также элементами другого множества. Например, множество {1, 2} является подмножеством множества {1, 2, 3}.

Что такое множество в дискретной математике?

Множество в дискретной математике — это совокупность различных объектов, которые называются элементами множества. В отличие от упорядоченных списков, элементы множества не имеют определенного порядка.