Что такое множество в математике 3

Множество в математике — это упорядоченная коллекция объектов, которая может быть конечной или бесконечной. В статье

Множество — это основное понятие в математике, которое описывает совокупность элементов, объединенных каким-либо общим свойством. Множество может содержать различные объекты — числа, буквы, предметы и т.д. В математике множество обозначается заглавной буквой латинского алфавита, а элементы множества записываются в фигурных скобках и разделяются запятыми.

Множества обладают рядом свойств и операций. Одно из основных свойств множества — уникальность элементов, то есть каждый элемент может входить в множество только один раз. Кроме того, множество может быть конечным или бесконечным. Операции над множествами включают объединение, пересечение и разность. Объединение двух множеств содержит все элементы обоих множеств, пересечение — только общие элементы, а разность — элементы первого множества, которых нет во втором.

Примерами множеств могут быть: множество натуральных чисел, множество цветов радуги, множество геометрических фигур и т.д. Математика активно использует множества для решения различных задач, а также для построения других математических объектов, таких как функции и отношения. Понимание множеств и их свойств является фундаментальным для изучения математики и других наук.

Определение множества в математике

Основными элементами множества являются его элементы или члены. Элементы множества могут быть любого типа: числа, буквы, слова, объекты, другие множества и так далее.

В математике множество обычно обозначается заглавными латинскими буквами, например, A, B, C. Для указания принадлежности элемента к множеству используется символ ∈ («принадлежит»), а для указания отсутствия принадлежности — символ ∉ («не принадлежит»).

Множество может быть описано явно или неявно. Явное описание множества представляет собой перечисление всех его элементов в фигурных скобках, например, A = {1, 2, 3}. Неявное описание множества основано на задании свойств его элементов, например, B = {x | x является четным числом}.

Важным свойством множества является то, что оно не содержит повторяющихся элементов. Если элемент встречается в множестве более одного раза, он считается только одним из его элементов.

Множество может быть конечным или бесконечным. Конечное множество содержит конечное количество элементов, например, C = {a, b, c}. Бесконечное множество содержит бесконечное количество элементов, например, D = {1, 2, 3, …}.

Множество может быть пустым или непустым. Пустое множество не содержит ни одного элемента и обозначается символом ∅ или {}.

Множество может быть задано с помощью списка элементов, условия, функции или другими способами. Оно может быть объединено с другими множествами операцией объединения, пересечено с другими множествами операцией пересечения, разделено на подмножества и так далее.

Свойства множества в математике

1. Равенство множеств: Два множества считаются равными, если они содержат одни и те же элементы. То есть, если каждый элемент первого множества принадлежит второму множеству, и каждый элемент второго множества принадлежит первому множеству.

2. Пустое множество: Это множество, которое не содержит ни одного элемента. Оно обозначается символом ∅ или {}.

3. Непустое множество: Множество, содержащее хотя бы один элемент.

4. Подмножество: Множество A является подмножеством множества B, если каждый элемент множества A также является элементом множества B. Обозначается как A ⊆ B.

5. Надмножество: Множество A является надмножеством множества B, если каждый элемент множества B также является элементом множества A. Обозначается как A ⊇ B.

6. Дополнение множества: Дополнение множества A относительно универсального множества U — это множество элементов, которые принадлежат U, но не принадлежат A. Обозначается как A’ или complement(A).

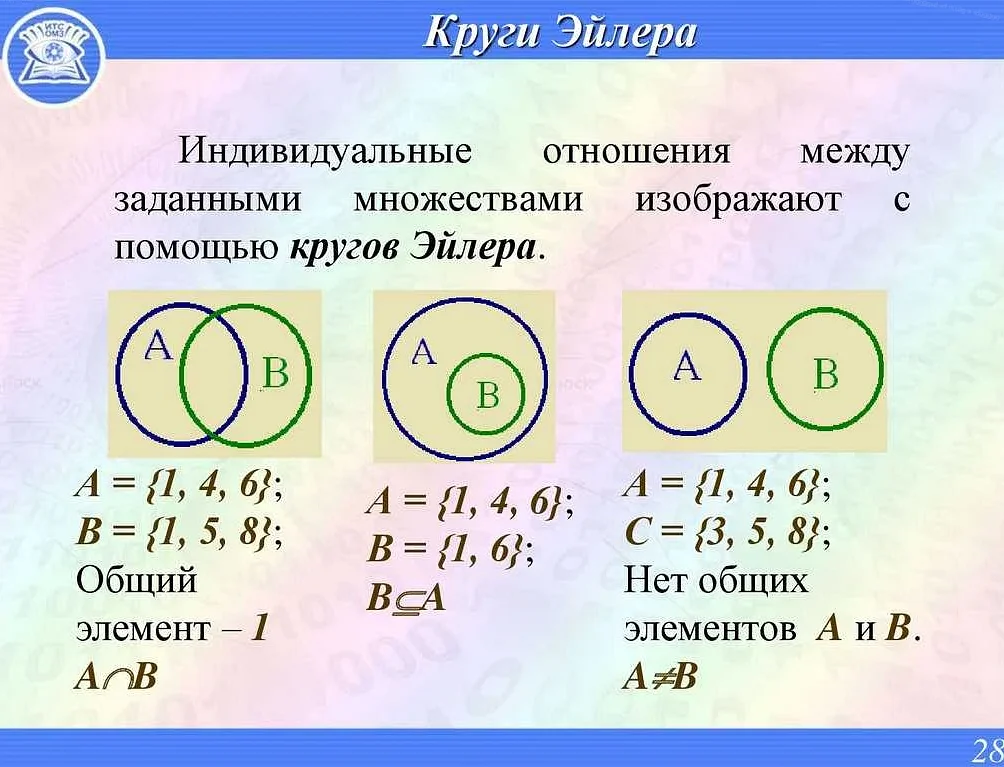
7. Пересечение множеств: Пересечение двух множеств A и B — это множество элементов, которые принадлежат одновременно и A, и B. Обозначается как A ∩ B.

8. Объединение множеств: Объединение двух множеств A и B — это множество элементов, которые принадлежат либо A, либо B, либо одновременно A и B. Обозначается как A ∪ B.

9. Разность множеств: Разность множеств A и B — это множество элементов, которые принадлежат множеству A, но не принадлежат множеству B. Обозначается как A \ B или A — B.

10. Декартово произведение: Декартово произведение двух множеств A и B — это множество всех упорядоченных пар (a, b), где a принадлежит A, а b принадлежит B. Обозначается как A × B.

Мощность множества и операции над множествами

Операции над множествами позволяют выполнять различные действия с множествами. Основными операциями над множествами являются объединение, пересечение, разность и дополнение.

Объединение двух множеств A и B обозначается как A ∪ B и представляет собой множество, состоящее из всех элементов, которые принадлежат либо множеству A, либо множеству B, либо обоим множествам одновременно.

Пересечение двух множеств A и B обозначается как A ∩ B и представляет собой множество, состоящее из всех элементов, которые принадлежат и множеству A, и множеству B одновременно.

Разность двух множеств A и B обозначается как A \ B и представляет собой множество, состоящее из всех элементов, которые принадлежат множеству A, но не принадлежат множеству B.

Дополнение множества A обозначается как A’ или complement(A) и представляет собой множество, состоящее из всех элементов, которые не принадлежат множеству A, но принадлежат универсальному множеству.

ОперацияОбозначениеОписание

Объединение	A ∪ B	Множество всех элементов, которые принадлежат A или B или обоим множествам
Пересечение	A ∩ B	Множество всех элементов, которые принадлежат и A и B одновременно
Разность	A \ B	Множество всех элементов, которые принадлежат A, но не принадлежат B
Дополнение	A’	Множество всех элементов, которые не принадлежат A, но принадлежат универсальному множеству

Принципы построения множеств

1. Принцип об абстракции. Множество строится на основе выделения общего признака у элементов. Например, можно построить множество всех четных чисел, где каждый элемент имеет общий признак — делится на 2 без остатка.

2. Принцип описательного определения. Множество может быть построено путем описания его элементов. Например, можно построить множество всех столиц стран мира, перечислив каждую столицу в описании множества.

3. Принцип перечисления элементов. Множество может быть построено путем перечисления всех его элементов. Например, можно построить множество всех гласных букв в русском алфавите, перечислив их: а, е, ё, и, о, у, ы, э, ю, я.

4. Принцип включения или исключения элементов. Множество может быть построено путем указания, какие элементы входят в него, а какие исключаются. Например, можно построить множество всех двузначных чисел, включая как положительные, так и отрицательные, исключая ноль.

Эти принципы помогают систематизировать и классифицировать множества, делая их более удобными для работы и анализа в математике.

Примеры множеств в математике

Множество натуральных чисел: Множество всех положительных целых чисел, начиная с единицы: {1, 2, 3, 4, …}.

Множество целых чисел: Множество всех целых чисел, включая нуль и отрицательные числа: {…, -3, -2, -1, 0, 1, 2, 3, …}.

Множество рациональных чисел: Множество всех чисел, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами: {…, -2/3, -1/2, -1/3, 0, 1/3, 1/2, 2/3, …}.

Множество действительных чисел: Множество всех чисел, которые можно представить на числовой прямой, включая иррациональные числа, такие как корень из двух и число «пи»: {…, -√2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, √2, 3.14, …}.

Множество комплексных чисел: Множество всех чисел вида a + bi, где a и b являются действительными числами, а i — мнимая единица, такая что i^2 = -1: {…, -3 — 2i, -2 — i, -1, 0, 1, 2 + i, 3 + 2i, …}.

Множество пустое: Множество, не содержащее ни одного элемента, обозначается {} или ∅.

Множество всех множеств: Множество, содержащее все возможные множества, называется универсальным множеством и обозначается U.

Множество подмножеств: Множество, содержащее все подмножества данного множества, называется множеством всех подмножеств и обозначается P(A).

Множество декартова произведения: Множество, состоящее из всех возможных упорядоченных пар элементов из двух или более множеств, обозначается A × B.

Множество всех букв алфавита: Множество всех букв алфавита, состоящее из однобуквенных элементов.

Бесконечные множества и их свойства

Свойство 1: Бесконечность

Бесконечные множества содержат бесконечное количество элементов, которые могут быть перечислены или охарактеризованы. Например, множество натуральных чисел {1, 2, 3, …} является бесконечным, так как можно продолжать перечислять натуральные числа бесконечно.

Свойство 2: Подмножества

Бесконечные множества могут содержать бесконечное количество подмножеств. Например, множество всех натуральных чисел содержит подмножества четных чисел, нечетных чисел, простых чисел и так далее.

Свойство 3: Биекция с частью себя

Бесконечные множества могут быть биективно отображены с их собственными подмножествами. Например, множество натуральных чисел можно биективно отобразить со множеством четных натуральных чисел, где каждому натуральному числу соответствует удвоенное число.

Свойство 4: Бесконечность при удалении конечного числа элементов

Бесконечное множество остается бесконечным, даже если из него удалить конечное число элементов. Например, множество натуральных чисел остается бесконечным, даже если из него удалить несколько чисел.

Свойство 5: Показательная мощность

Бесконечные множества могут иметь разную мощность. Например, множество всех натуральных чисел имеет мощность континуума, то есть равно мощности множества всех действительных чисел.

Бесконечные множества и их свойства играют важную роль в математике и имеют широкие приложения в различных областях науки.

Виды множеств по элементам и структуре

В зависимости от свойств и характеристик элементов, а также структуры, множества могут быть разделены на несколько видов:

• Конечные и бесконечные множества: конечное множество содержит определенное количество элементов, в то время как бесконечное множество имеет неограниченное количество элементов.
• Равномощные множества: два множества считаются равномощными, если между их элементами можно установить взаимно однозначное соответствие.
• Подмножества: множество A называется подмножеством множества B, если каждый элемент A также является элементом B.
• Декартово произведение: произведение двух множеств A и B состоит из всех возможных упорядоченных пар (a, b), где a — элемент A, b — элемент B.
• Пустое множество: множество, не содержащее ни одного элемента, называется пустым множеством или нулевым множеством.
• Универсальное множество: множество, содержащее все возможные элементы, которые рассматриваются в данном контексте, называется универсальным множеством.

Классификация множеств по элементам и структуре позволяет систематизировать и изучать их свойства, а также использовать различные методы и операции для работы с множествами в математике.

Практическое применение множеств в различных областях

Математика: Множества используются для определения отношений между объектами, решения задач комбинаторики, анализа данных и доказательства теорем. Они играют важную роль в теории множеств и многих других разделах математики.

Логика и информатика: Множества используются в логических операциях, алгоритмах поиска и сортировки данных, а также в структурах данных, таких как хэш-таблицы и графы.

Экономика: Множества применяются для моделирования экономических процессов, таких как потребление, производство и распределение ресурсов. Они используются для анализа рыночных трендов, прогнозирования спроса и предложения, а также для принятия решений в области инвестиций и финансов.

Искусственный интеллект: Множества применяются в алгоритмах машинного обучения для классификации данных, кластеризации и поиска закономерностей. Они используются для создания моделей и прогнозирования результатов на основе имеющихся данных.

Сети и телекоммуникации: Множества применяются для моделирования связей и взаимодействий между узлами в сетях, таких как компьютерные сети, интернет и телефонные сети. Они используются для оптимизации маршрутизации, распределения трафика и прогнозирования нагрузки.

Биология: Множества применяются для классификации организмов в таксономии, анализа генетических данных, моделирования биологических процессов и исследования эволюции.

Это лишь некоторые примеры практического применения множеств в различных областях. Без множеств многие современные науки и технологии были бы невозможны.

Вопрос-ответ:

Что такое множество в математике?

Множество в математике — это совокупность элементов, объединенных общим признаком.

Какие свойства имеют множества?

Множества могут быть конечными или бесконечными, содержать различные элементы или быть пустыми. Они не зависят от порядка элементов и не содержат повторяющиеся элементы.

Как можно описать множество?

Множество можно описать перечислением всех его элементов, использованием характеристического свойства или с помощью операций над другими множествами.

Какие примеры множеств можно привести?

Примерами множеств могут быть множество всех целых чисел, множество всех красных фруктов, множество всех простых чисел и т. д.

Какие операции можно выполнять над множествами?

Операции над множествами включают объединение, пересечение, разность и дополнение. Эти операции позволяют комбинировать и анализировать множества.

Видео по теме: