Что такое натуральное число 5 класс в математике

В математике натуральные числа — это целые числа, которые начинаются с единицы и продолжаются бесконечно. Натуральное число 5 класс включает в себя все числа, которые можно записать без использования десятичной точки или знака минус. В этой статье вы узнаете подробности о натуральных числах и их применении в математике.

Математика — это наука, которая изучает числа, их свойства и взаимоотношения. Одним из важных понятий, которое изучают в начальной школе, является натуральное число. Натуральные числа — это положительные целые числа, которые используются для подсчета и упорядочивания объектов. Они обозначают количество элементов в множестве и являются основой для понимания других разделов математики.

В 5 классе ученики углубляют свои знания о натуральных числах. Они учатся сравнивать числа, находить их сумму и разность, а также умножать и делить. Работа с натуральными числами помогает развить логическое мышление, абстрактное мышление и навыки решения математических задач.

Примеры натуральных чисел:

1 — это наименьшее натуральное число, которое указывает на один объект или элемент.

2 — указывает на два объекта или элемента.

3 — указывает на три объекта или элемента.

4 — указывает на четыре объекта или элемента.

5 — указывает на пять объектов или элементов.

Натуральные числа используются в повседневной жизни для подсчета количества предметов, людей, времени и многого другого. Понимание и умение работать с натуральными числами является важным навыком, который поможет ученикам не только в математике, но и в других областях знания.

Основные понятия о натуральных числах в математике 5 класса

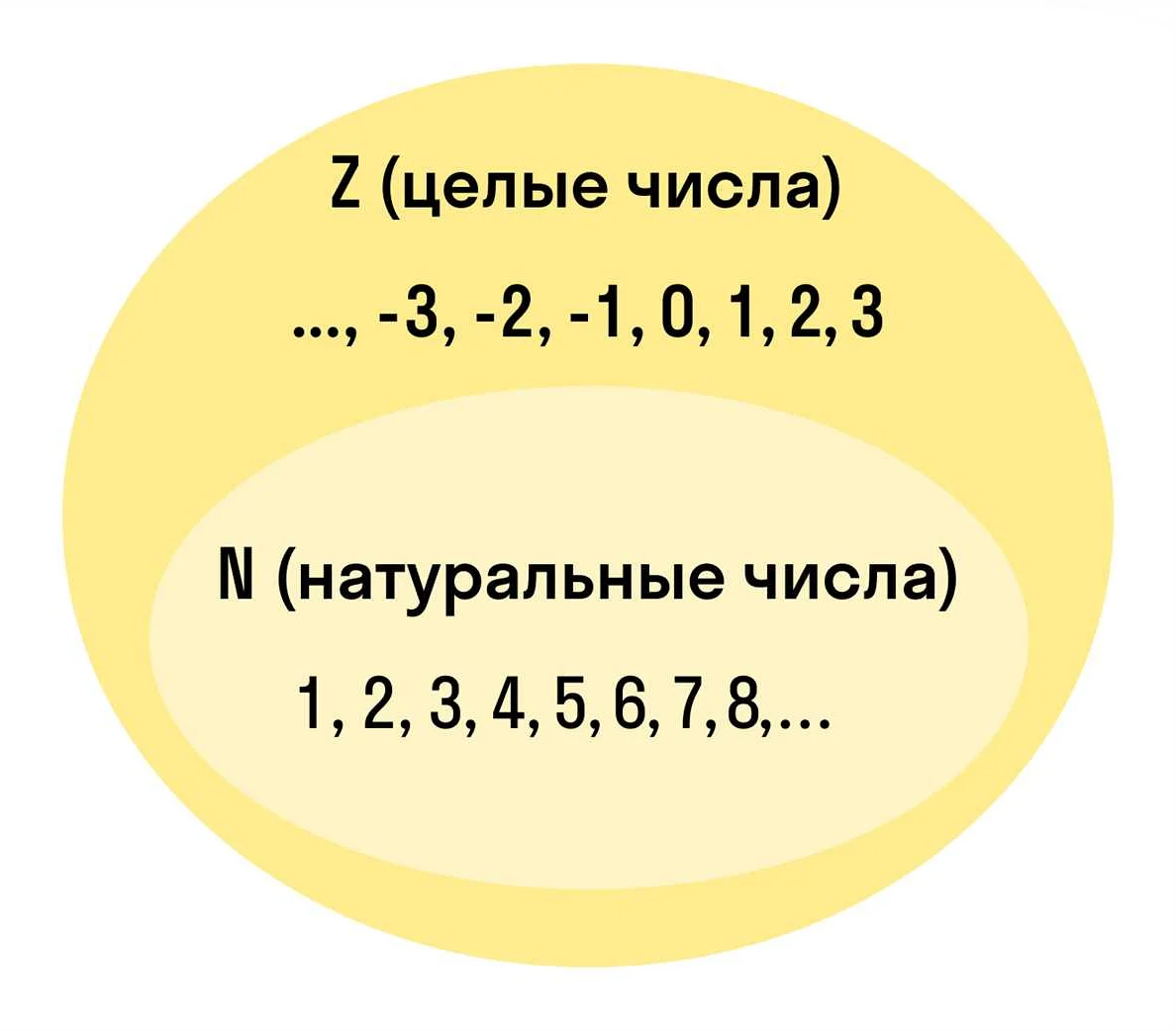
Натуральные числа можно представить в виде числовой прямой, где число 1 находится крайней левой точкой, а остальные числа расположены в порядке возрастания.

Основные операции с натуральными числами включают сложение, вычитание, умножение и деление. Например, при сложении двух натуральных чисел получается третье число, которое обозначает сумму предметов или явлений.

Также натуральные числа можно сравнивать между собой. Например, если у нас есть два предмета, то их количество обозначается числом 2, которое больше числа 1 и меньше числа 3.

В математике также используются термины «четное число» и «нечетное число». Четные числа делятся нацело на 2, например, 2, 4, 6 и так далее. Нечетные числа не делятся на 2 без остатка, например, 1, 3, 5 и так далее.

Натуральные числа играют важную роль в математике и используются в различных областях знаний, таких как геометрия, алгебра и статистика. Понимание основных понятий о натуральных числах поможет ученикам развить математическое мышление и навыки решения задач.

Видео по теме:

Классификация натуральных чисел

Натуральные числа можно классифицировать по различным признакам:

1. Однозначные числа — числа, которые содержат всего одну цифру. Например, 1, 2, 3, и так далее.
2. Двузначные числа — числа, которые содержат две цифры. Например, 10, 11, 12, и так далее.
3. Трехзначные числа — числа, которые содержат три цифры. Например, 100, 101, 102, и так далее.

Кроме того, натуральные числа можно разделить на четные и нечетные:

• Четные числа — числа, которые делятся на 2 без остатка. Например, 2, 4, 6, и так далее.
• Нечетные числа — числа, которые не делятся на 2 без остатка. Например, 1, 3, 5, и так далее.

Также, натуральные числа можно классифицировать как простые и составные:

• Простые числа — числа, которые имеют только два делителя: 1 и само число. Например, 2, 3, 5, и так далее.
• Составные числа — числа, которые имеют больше двух делителей. Например, 4, 6, 8, и так далее.

Определение натурального числа

Натуральные числа обозначаются символами 1, 2, 3, 4 и так далее. Они используются, например, для подсчета количества людей, предметов, животных и других объектов в реальном мире.

Примеры натуральных чисел:

• Число 1 – означает один элемент или единицу чего-либо.
• Число 2 – означает два элемента или две единицы чего-либо.
• Число 3 – означает три элемента или три единицы чего-либо.
• И так далее.

Натуральные числа являются одним из основных понятий в математике, и они широко применяются в различных областях, таких как арифметика, геометрия, алгебра и т.д.

Свойства натуральных чисел

Натуральные числа обладают рядом особых свойств, которые помогают нам лучше понять их природу и взаимодействие друг с другом.

• Свойство упорядоченности: Натуральные числа можно расположить в порядке возрастания или убывания. Например, числа 1, 2, 3, 4, 5 идут по возрастанию, а числа 5, 4, 3, 2, 1 идут по убыванию.
• Свойство соседства: У каждого натурального числа есть соседи — предыдущее и следующее число. Например, для числа 5 предыдущим будет 4, а следующим — 6.
• Свойство пропорциональности: Натуральные числа могут быть умножены или поделены друг на друга с сохранением своего натурального характера. Например, если умножить число 5 на 2, получится число 10, которое также является натуральным.
• Свойство сравнимости: Натуральные числа можно сравнивать между собой. Например, число 5 больше числа 3, а число 2 меньше числа 4.
• Свойство сложения и вычитания: Натуральные числа можно складывать и вычитать друг из друга. Например, 5 + 3 = 8, а 8 — 3 = 5.

Эти свойства натуральных чисел помогают нам решать различные задачи и оперировать числами в математике.

Натуральные числа в повседневной жизни

Вот несколько примеров использования натуральных чисел в повседневной жизни:

1. Когда мы считаем количество яблок в корзине или количество книг на полке, мы используем натуральные числа.
2. Когда мы считаем количество друзей на вечеринке или количество учеников в классе, мы также используем натуральные числа.
3. Если мы хотим узнать, сколько денег у нас есть в кошельке, мы снова используем натуральные числа.
4. Когда мы считаем количество дней до нашего дня рождения или количество месяцев в году, мы также используем натуральные числа.

Натуральные числа помогают нам ориентироваться в мире и делать различные расчеты. Они являются основой для изучения более сложных математических концепций и помогают нам понимать мир вокруг нас.

Примеры использования натуральных чисел в задачах

Натуральные числа широко применяются в различных математических задачах. Рассмотрим несколько примеров использования натуральных чисел:

• Задача 1: В магазине было 10 яблок, али 5 из них продали. Сколько яблок осталось в магазине?
• Задача 2: У Маши было 7 карандашей, а у Пети было в два раза больше. Сколько карандашей было у Пети?
• Задача 3: У Васи было 15 конфет, а он раздал по 3 конфеты каждому другу. Сколько конфет осталось у Васи?

В решении этих задач мы используем операции над натуральными числами, такие как сложение, вычитание и умножение. Натуральные числа позволяют нам считать предметы, людей, дни и многое другое. Они являются основным инструментом в изучении математики и применяются во многих сферах нашей жизни.

Основные операции с натуральными числами

В математике существует несколько основных операций, которые можно выполнять с натуральными числами.

Сложение — это операция, при которой два или более числа объединяются в одно число, называемое суммой. Например, 2 + 3 = 5.

Вычитание — это операция, при которой одно число вычитается из другого числа, результат называется разностью. Например, 5 — 2 = 3.

Умножение — это операция, при которой одно число увеличивается в заданное количество раз. Результат умножения называется произведением. Например, 2 * 3 = 6.

Деление — это операция, при которой одно число делится на другое число. Результат деления называется частным. Например, 6 / 3 = 2.

Остаток от деления — это операция, при которой одно число делится на другое число, и остается некоторое число, которое не делится нацело. Например, остаток от деления 7 на 3 равен 1.

Для выполнения этих операций над натуральными числами нужно знать основные свойства и правила математики. Например, сумма двух натуральных чисел всегда будет натуральным числом, а разность может быть натуральным числом или нулем.

Также важно уметь правильно записывать операции с натуральными числами и выполнять их последовательно, чтобы получить правильный результат.

Примеры решения задач с использованием натуральных чисел

1. Задача: На площадке для игры в футбол есть 8 игроков. Сколько игроков должно стоять на поле, если каждая команда играет в полным составом?

Решение: Поскольку каждая команда играет в полном составе, на поле должно быть по 11 игроков. Всего на поле должно стоять 11 + 11 = 22 игрока.

2. Задача: В корзине лежат 36 яблок. Каждый день из корзины берут по 4 яблока. Сколько яблок останется в корзине через 7 дней?

Решение: Каждый день из корзины берут по 4 яблока, значит за 7 дней будет взято 4 * 7 = 28 яблок. Остаток яблок в корзине равен 36 — 28 = 8 яблок.

3. Задача: В классе 25 учеников. Каждый день по 5 учеников пропускают урок. Сколько учеников пропустит урок класс в течение 5 дней?

Решение: Каждый день пропускают урок по 5 учеников, значит за 5 дней будет пропущено 5 * 5 = 25 учеников.

Значимость изучения натуральных чисел в математике 5 класса

Натуральные числа — это числа, которые используются для обозначения количества предметов или объектов. Они начинаются с единицы и продолжаются бесконечно: 1, 2, 3, 4, 5, и так далее. Изучение натуральных чисел позволяет ученикам развить навыки счета, операций сложения и вычитания, а также понимание последовательности чисел.

Основная цель изучения натуральных чисел в 5 классе — научить учеников работать с числами, понимать их свойства и особенности. Это поможет им развить логическое мышление, абстрактное мышление и аналитические навыки, которые будут полезны в дальнейшем изучении математики и других наук.

Изучение натуральных чисел также помогает ученикам развить навыки решения задач. При работе с натуральными числами они учатся анализировать задачи, определять необходимую информацию, использовать различные стратегии решения и проверять правильность полученного результата. Эти навыки помогут ученикам не только в математике, но и в реальной жизни, где встречаются различные задачи, требующие математического мышления и решения.

Примеры задач, связанных с натуральными числами:

1. В корзине лежит 7 яблок, а в другой корзине — 4 яблока. Сколько яблок всего?

2. Аня собрала 5 красных шариков, а Петя — 3 желтых шарика. Сколько шариков у них всего?

3. У Васи было 9 марок, а он отдал 3 марки другу. Сколько марок у Васи осталось?

Эти и подобные задачи помогают ученикам применять знания о натуральных числах на практике и развивать навыки решения различных математических задач.

Таким образом, изучение натуральных чисел в математике 5 класса является важным этапом в обучении математике, которое способствует развитию логического мышления, абстрактного мышления, аналитических навыков и навыков решения задач. Оно также помогает ученикам понять и использовать числа в различных практических ситуациях и задачах.

Вопрос-ответ:

Что такое натуральное число?

Натуральное число — это число, которое используется для обозначения количества элементов в конечном множестве. Оно может быть положительным и целым. Натуральные числа образуют бесконечную последовательность, начиная с единицы: 1, 2, 3, 4 и так далее.

Какие примеры можно привести натуральных чисел?

Некоторые примеры натуральных чисел: 1, 2, 3, 4, 5, 6 и так далее. Они используются для подсчета элементов в различных ситуациях, например, при счете яблок, книг, детей и т. д.

Какие основные понятия связаны с натуральными числами?

Основные понятия, связанные с натуральными числами, включают следующие: последовательность натуральных чисел, упорядоченность чисел, операции сложения и умножения натуральных чисел, свойства сложения и умножения, принципы ассоциативности и коммутативности, нулевой элемент, единичный элемент, деление с остатком и многое другое.

Как можно использовать натуральные числа в реальной жизни?

Натуральные числа используются в реальной жизни для подсчета и измерения различных вещей. Например, вы можете использовать натуральные числа для подсчета количества яблок в корзине, книг в библиотеке, друзей на вечеринке и т. д. Они также могут быть использованы для измерения времени, расстояния и других физических величин.