Что такое в математике нод и нок 6 класс

Нод и нок в математике – это два важных понятия, которые изучаются в 6 классе. Нод (наибольший общий делитель) и нок (наименьшее общее кратное) помогают решать задачи на делимость чисел и находить общие множители и кратные. Узнайте, как найти нод и нок чисел, и как применять эти знания в практических задачах.

НОД (наибольший общий делитель) и НОК (наименьшее общее кратное) – это два важных понятия в математике, которые помогают нам находить общие свойства чисел и делать различные вычисления. Знать эти понятия очень полезно для решения различных задач и заданий по математике.

Наибольший общий делитель двух или более чисел – это наибольшее число, на которое все заданные числа делятся без остатка. Например, для чисел 12 и 18 наибольший общий делитель равен 6, так как оба числа делятся нацело на 6.

Наименьшее общее кратное двух или более чисел – это наименьшее число, которое делится нацело на все заданные числа. Например, для чисел 4 и 6 наименьшее общее кратное равно 12, так как 12 делится нацело на оба заданных числа.

Определение НОД и НОК помогает нам решать различные задачи, связанные с дробями, делимостью чисел, простыми и составными числами, и многим другим. Эти понятия являются основой для понимания дальнейших математических концепций и помогают нам лучше разбираться в мире чисел и их свойств.

Что означает НОД?

Другими словами, НОД — это наибольшее число, на которое без остатка делятся два или более числа.

НОД часто используется для сокращения дробей, нахождения наименьшего общего кратного (НОК) и решения различных задач в математике.

Например, для чисел 12 и 18, наибольший общий делитель будет 6, потому что 6 делится и на 12, и на 18 без остатка.

Чтобы найти НОД, можно использовать различные методы, такие как поиск общих делителей чисел, факторизация чисел или метод Евклида.

Видео по теме:

Что означает НОК?

НОК часто используется в математике для решения задач, связанных с периодичностью и повторяемостью событий. Он также может быть полезен при работе с дробями и расчете времени, например, для определения момента, когда два события произойдут одновременно или снова повторятся одновременно.

Для нахождения НОК двух или более чисел можно использовать метод поиска их общего кратного. Сначала находим все кратные каждого числа, затем выбираем наименьшее число из всех этих кратных, которое будет НОК заданных чисел.

Пример:

• Найти НОК чисел 6 и 8.
• Кратные числа 6: 6, 12, 18, 24, 30, 36, …
• Кратные числа 8: 8, 16, 24, 32, 40, 48, …
• Общие кратные числа: 24, 48, 72, …
• Наименьшее общее кратное: 24.

Таким образом, НОК чисел 6 и 8 равен 24.

Важно отметить, что НОК не является уникальным для заданных чисел, их может быть бесконечное количество. Однако в большинстве задач требуется найти наименьшее общее кратное.

Как найти НОД двух чисел?

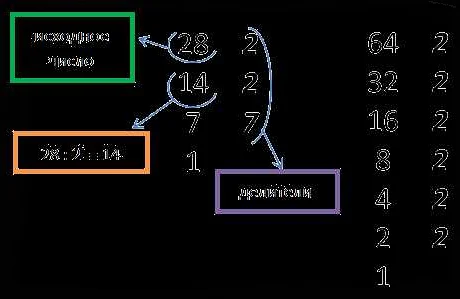
НОД (наибольший общий делитель) двух чисел можно найти с помощью нескольких методов.

Метод деления: для нахождения НОД двух чисел, необходимо разделить большее число на меньшее. Если деление происходит без остатка, то НОД равен меньшему числу. Если есть остаток, то его необходимо разделить на меньшее число и продолжить деление до тех пор, пока остаток не станет равным нулю. Последнее ненулевое число будет НОДом.

Метод вычитания: для нахождения НОД двух чисел, необходимо из большего числа вычитать меньшее. Если результат больше нуля, то его следует заменить на новое большее число, которое получается после вычитания. Процесс повторяется до тех пор, пока числа не станут равными. Полученное число будет НОДом.

Метод простых множителей: для нахождения НОД двух чисел, необходимо разложить их на простые множители и найти общие множители. НОД будет равен произведению этих общих множителей.

Пример:

Даны числа 24 и 36.

Метод деления:

36 / 24 = 1 (остаток 12)

24 / 12 = 2 (остаток 0)

НОД = 12

Метод вычитания:

36 — 24 = 12

24 — 12 = 12

НОД = 12

Метод простых множителей:

24 = 2 * 2 * 2 * 3

36 = 2 * 2 * 3 * 3

Общие множители: 2, 2, 3

НОД = 2 * 2 * 3 = 12

Пример нахождения НОД

НОД (наибольший общий делитель) двух чисел можно найти с помощью алгоритма Евклида. Рассмотрим пример нахождения НОД чисел 18 и 24.

ШагДелениеДелительОстаток

1	24 ÷ 18	18	6
2	18 ÷ 6	6	0

На первом шаге мы делим 24 на 18 и получаем остаток 6. Затем на втором шаге делим 18 на 6 и получаем остаток 0. Когда остаток становится равным 0, последний делитель (6) является НОД чисел 18 и 24.

Таким образом, НОД чисел 18 и 24 равен 6.

Как найти НОК двух чисел?

Первый метод — это разложение чисел на простые множители. Найдем простые множители для каждого числа и запишем их в виде степени:

Пример: Найти НОК для чисел 12 и 15.

12 = 2^2 * 3

15 = 3 * 5

Записываем все простые множители в виде степени с максимальными показателями:

2^2 * 3 * 5 = 60

Таким образом, НОК для чисел 12 и 15 равен 60.

Второй метод — это использование формулы НОК(a, b) = (a * b) / НОД(a, b), где НОД — наибольший общий делитель. Найдем НОД для чисел 12 и 15:

НОД(12, 15) = 3

Используя формулу НОК(a, b) = (a * b) / НОД(a, b), получаем:

НОК(12, 15) = (12 * 15) / 3 = 60

Таким образом, результат получен с использованием формулы НОК(a, b) = (a * b) / НОД(a, b) также равен 60.

Теперь вы знаете, как найти НОК двух чисел! Это может пригодиться, например, для решения задач на кратные числа или для нахождения общего времени встречи двух человек.

Пример нахождения НОК

Для нахождения НОК (наименьшего общего кратного) двух чисел нужно выполнить следующие шаги:

1. Найдите все простые множители каждого из чисел.
2. Укажите каждый простой множитель с наибольшей степенью.
3. Умножьте все полученные простые множители вместе.

Рассмотрим пример нахождения НОК для чисел 12 и 18:

1. Простые множители числа 12: 2 и 3.
2. Простые множители числа 18: 2 и 3.
3. Наибольшие степени простых множителей: 2^2 и 3^1.
4. Умножение: 2^2 * 3^1 = 4 * 3 = 12.

Таким образом, НОК для чисел 12 и 18 равен 12.

Зачем нужны НОД и НОК?

НОД используется для нахождения наибольшего числа, на которое делятся два или более числа без остатка. Он позволяет сократить дроби до несократимого вида и найти общие делители двух чисел. Например, если нужно разделить пирог на одинаковые кусочки, НОД поможет найти наибольший размер кусочка, чтобы все было равномерно поделено.

НОК находит наименьшее общее кратное двух или более чисел. Он используется, когда нужно найти общий множитель двух чисел, например, при расчете времени, через которое две или более вещи совершат одно и то же действие вместе. Например, если нужно синхронизировать два часа, чтобы они звонили одновременно, НОК поможет найти наименьшее время, через которое они зазвонят вместе.

Оба этих понятия являются основными инструментами для решения задач по арифметике, алгебре и другим областям математики.

Вопрос-ответ:

Что такое НОД и НОК?

НОД (наибольший общий делитель) двух или более чисел — это наибольшее число, которое одновременно делит все эти числа без остатка. НОК (наименьшее общее кратное) — это наименьшее число, которое делится на все эти числа без остатка.

Как найти НОД и НОК двух чисел?

Чтобы найти НОД двух чисел, нужно разложить каждое число на простые множители и найти их общие множители с наибольшей степенью. Например, НОД чисел 12 и 18 равен 6, потому что 12 = 2^2 * 3, 18 = 2 * 3^2, и общий множитель 2 встречается с наибольшей степенью 1, общий множитель 3 встречается с наибольшей степенью 1, поэтому 2 * 3 = 6. Чтобы найти НОК двух чисел, нужно разложить каждое число на простые множители и найти их общие множители с наименьшей степенью. Например, НОК чисел 12 и 18 равен 36, потому что 12 = 2^2 * 3, 18 = 2 * 3^2, и общий множитель 2 встречается с наименьшей степенью 1, общий множитель 3 встречается с наименьшей степенью 1, поэтому 2^2 * 3^2 = 36.

Приведите примеры вычисления НОД и НОК.

Пример вычисления НОД: Найти НОД чисел 24 и 36. Разложим 24 на простые множители: 24 = 2^3 * 3. Разложим 36 на простые множители: 36 = 2^2 * 3^2. Общий множитель 2 встречается с наибольшей степенью 2, общий множитель 3 встречается с наибольшей степенью 1, поэтому НОД равен 2^2 * 3 = 12. Пример вычисления НОК: Найти НОК чисел 24 и 36. Разложим 24 на простые множители: 24 = 2^3 * 3. Разложим 36 на простые множители: 36 = 2^2 * 3^2. Общий множитель 2 встречается с наименьшей степенью 2, общий множитель 3 встречается с наименьшей степенью 1, поэтому НОК равен 2^3 * 3^2 = 72.

Зачем нужно знать НОД и НОК?

Знание НОД и НОК помогает в решении задач на поиск общего кратного или общего делителя нескольких чисел. Например, при делении предметов на равные группы, при распределении ресурсов, при вычислении времени, через которое две события произойдут одновременно.

Что такое НОД?

НОД (Наибольший Общий Делитель) двух или нескольких чисел — это наибольшее число, которое одновременно является делителем для всех этих чисел.