Что такое острый угол в математике 3
Содержимое
- 1 Что такое острый угол в математике 3
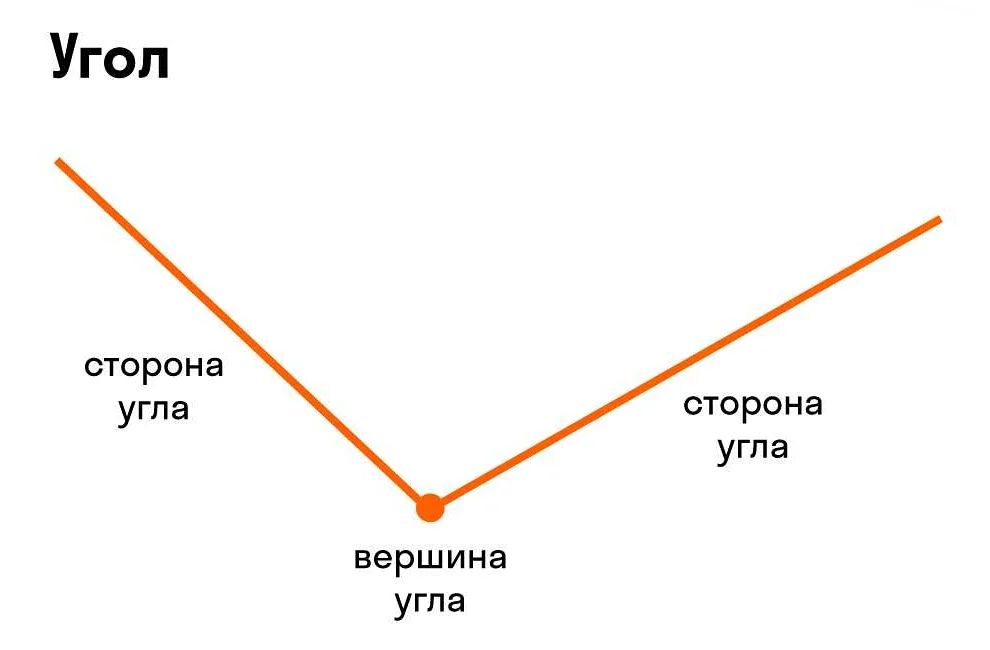
Острый угол в математике 3 — это угол, который меньше 90 градусов. Узнайте, как определить острый угол и используйте его свойства для решения задач и построения геометрических фигур.
Острый угол – это угол, значение которого меньше 90 градусов. В математике острый угол является одним из трех видов углов, в зависимости от его величины. Острый угол можно встретить в различных задачах и примерах из геометрии, физики, тригонометрии и других областей науки.
Острый угол можно представить как поворот одной прямой относительно другой прямой, при этом конечные точки прямых остаются фиксированными. Между этими прямыми образуется угол, которому соответствуют определенные свойства и характеристики.
Примерами острого угла могут быть углы треугольника, где все три угла являются острыми. Например, углы треугольника ABC, где угол A равен 60 градусов, угол B равен 50 градусов и угол C равен 70 градусов, все являются острыми углами.
Свойства острого угла включают в себя то, что сумма всех трех углов треугольника равна 180 градусов, а также то, что острый угол не может быть больше 90 градусов. Знание острого угла и его свойств позволяет решать различные задачи и задания, связанные с геометрией и тригонометрией.
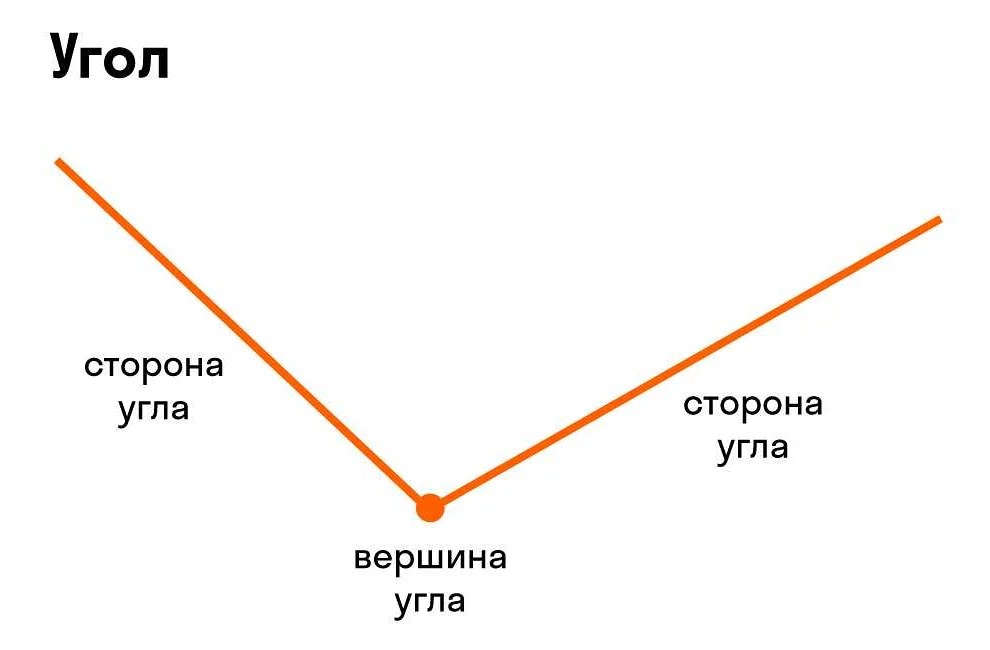
Определение острого угла
Острый угол можно представить с помощью геометрической фигуры — треугольника, где один из углов меньше 90 градусов.
Для определения острого угла можно использовать градусную меру, радианную меру или другие единицы измерения. В любом случае, если угол имеет меру меньше 90 градусов, он считается острым.
Острые углы имеют ряд свойств:
- Сумма мер всех углов треугольника равна 180 градусов. Если в треугольнике есть острый угол, то сумма мер двух других углов будет больше 90 градусов.
- Острый угол может быть углом между двумя сторонами прямоугольного треугольника.
- Острые углы можно измерять в градусах, минутах, секундах, радианах и других единицах измерения.
Примеры острых углов:
- Угол между стрелками часов, если время меньше 3 часов.
- Угол между двумя сторонами равнобедренного треугольника.
- Угол между двумя сторонами прямоугольного треугольника, если он не является прямым углом.
Примеры острых углов
ПримерИзображение
| Угол ABC |  |
| Угол DEF |  |
| Угол GHI |  |
Во всех приведенных примерах, значение угла меньше 90 градусов, поэтому они являются острыми углами.
Острый угол и его свойства
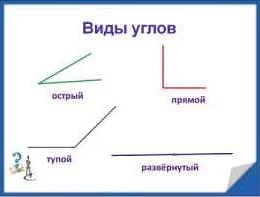
Острый угол обладает следующими свойствами:
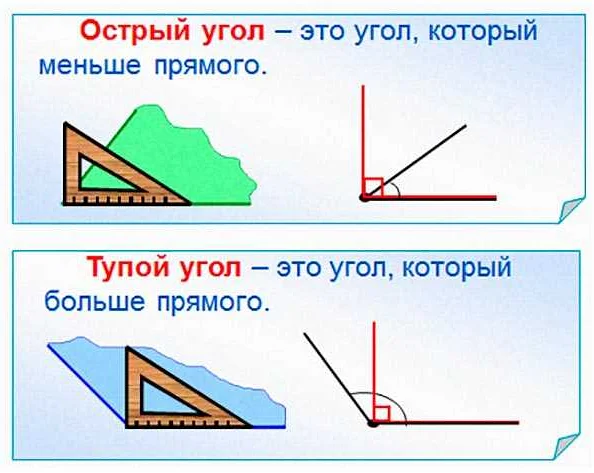
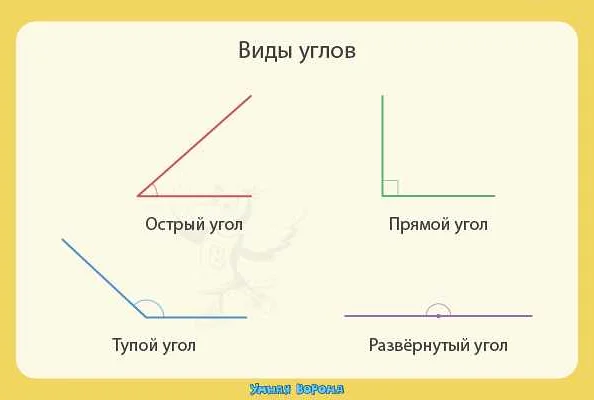
- Острый угол всегда имеет меру меньше 90 градусов.
- Сумма всех углов треугольника равна 180 градусов. Поэтому в остроугольном треугольнике сумма всех углов будет меньше 180 градусов.
- Острый угол может быть обозначен с помощью специальной обозначения, например, угол А может быть обозначен как ∠A.
- Острый угол может быть измерен с помощью транспортира или другого измерительного инструмента.
Примерами острого угла могут быть угол в равностороннем треугольнике, каждый из углов которого равен 60 градусов, а также угол в прямоугольном треугольнике, между катетами которого меньше 90 градусов.
Острый угол является важным понятием в геометрии и находит применение в различных областях науки и техники.
Острый угол и его измерение
Для измерения острого угла используется градусная мера. Градус — это единица измерения угла, которая равна 1/360 части полного оборота (равного 360 градусам). Таким образом, если угол составляет полный оборот, то его размер равен 360 градусам.
Чтобы измерить острый угол, используется градусный протектор или градусник. Градусник представляет собой полукруг с делениями от 0 до 180 градусов. Значение острого угла определяется по числу делений, на которое указывает градусник.
Размер углаОбозначение
| 0 градусов | угол равен 0 |
| 90 градусов | прямой угол |
| меньше 90 градусов | острый угол |
Например, если градусник указывает на 30 градусов, то это означает, что размер угла составляет 30 градусов и он является острым углом.
Острый угол имеет несколько свойств:
- Сумма острых углов треугольника равна 180 градусам.
- Острый угол может быть составной частью других углов, таких как тупой угол (больше 90 градусов) или полный угол (равный 360 градусам).
- Острый угол может быть измерен с помощью градусника или других инструментов для измерения углов.
Связь острого угла с другими понятиями
Острый угол связан с понятием треугольника. Треугольник, в котором все углы острые, называется остроугольным треугольником. Острый угол является одним из углов этого треугольника и обладает свойством, что его величина меньше 90 градусов.
Острый угол также связан с понятием синуса. Синус острого угла определяется как отношение противолежащего катета к гипотенузе прямоугольного треугольника, содержащего данный острый угол. Связь между острым углом и синусом позволяет использовать тригонометрические функции для нахождения значений острого угла в различных задачах.
Острые углы также связаны с понятием косинуса и тангенса. Косинус острого угла определяется как отношение прилежащего катета к гипотенузе прямоугольного треугольника, содержащего данный острый угол. Тангенс острого угла определяется как отношение противолежащего катета к прилежащему катету. Эти понятия позволяют более полно описать свойства и характеристики острого угла.
Острый угол также связан с понятием дополнительного угла. Дополнительный угол к острому углу является углом, который в сумме с ним равен 90 градусов. Знание свойств дополнительных углов позволяет решать задачи, связанные с острыми углами в различных контекстах.
Таким образом, острый угол имеет множество связей с другими понятиями, что позволяет более глубоко изучать его свойства и использовать его в различных математических задачах.
Применение острых углов в практике
В архитектуре острые углы используются при проектировании зданий и сооружений. Они позволяют определить форму и структуру здания, а также помогают в расчете нагрузок и давления на конструкции.
В инженерном деле острые углы применяются при разработке и проектировании различных механизмов и оборудования. Они позволяют определить углы наклона, направления движения и другие параметры, необходимые для правильной работы системы.
В картографии острые углы используются при составлении карт и планов местности. Они помогают определить углы поворота и направления объектов на карте, а также позволяют проводить точные измерения и расчеты расстояний.
В физике острые углы используются при изучении движения и силы. Они позволяют определить угол падения и отражения света, а также помогают в расчете силы трения и давления.
Таким образом, острые углы являются неотъемлемой частью математического и геометрического аппарата и находят широкое применение в практических ситуациях. Изучение острых углов позволяет улучшить понимание мира вокруг нас и применять математические знания на практике.
Значение острых углов в геометрии
Острые углы имеют ряд особенностей и свойств, которые являются основой для решения геометрических задач. Одно из наиболее известных свойств острого угла заключается в том, что сумма острых углов треугольника равна 180 градусов. Это свойство известно как «сумма углов треугольника».
Острые углы также используются для определения и классификации различных типов треугольников. Например, треугольник, у которого все углы острые, называется остроугольным треугольником. Остроугольные треугольники имеют ряд интересных свойств, таких как равенство биссектрис, теорема синусов и теорема косинусов.
Острые углы встречаются не только в треугольниках, но и в других геометрических фигурах, таких как прямоугольники, параллелограммы и равнобедренные треугольники. Острый угол также является одним из основных элементов при изучении тригонометрии.
В заключение, острые углы имеют важное значение в геометрии, так как они определяют форму и свойства различных фигур. Понимание острых углов позволяет решать геометрические задачи и проводить различные геометрические доказательства.
Выводы о острых углах
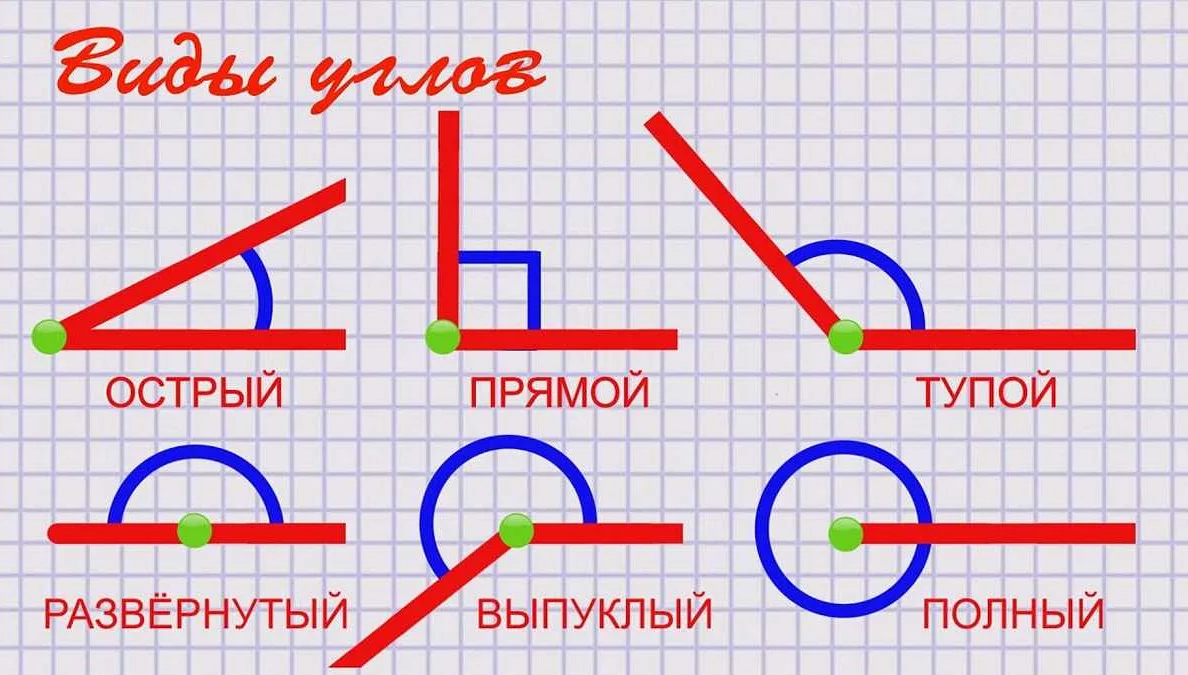
Острые углы имеют следующие свойства:
— Острые углы всегда меньше 90 градусов;
— Сумма трех острых углов в треугольнике равна 180 градусам;
— Чем меньше острый угол, тем меньше его синус, косинус и тангенс;
— Острые углы присутствуют во многих геометрических фигурах, например, в треугольниках, прямоугольных треугольниках, параллелограммах и т.д.
Острые углы имеют важное значение в геометрии и математике в целом. Изучение острых углов помогает понять взаимосвязь между углами и фигурами, а также применять их в различных задачах и вычислениях.
Видео по теме:
Что такое острый угол в математике?
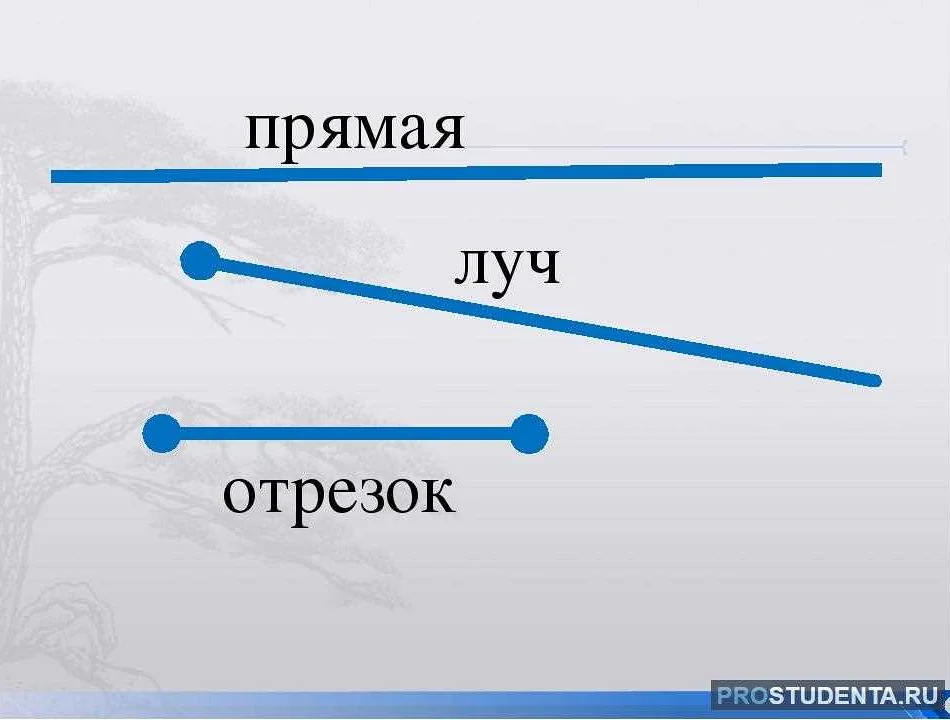
Острый угол в математике — это угол, чья мера меньше 90 градусов. Он образуется двумя лучами, выпущенными из одной точки и лежащими по одну сторону от общего отрезка.
Как можно понять, что угол острый?
Чтобы определить, что угол острый, нужно измерить его меру и убедиться, что она меньше 90 градусов.
Можете привести пример острого угла?
Конечно! Примером острого угла может быть угол, образованный стрелками часов, когда время показывает 9 часов.



Очень интересная статья! Я всегда думала, что острый угол — это просто маленький угол, но оказывается, это намного больше! Спасибо, что подробно объяснили определение острого угла и привели примеры. Теперь я лучше понимаю, что такое острый угол и как его можно распознать. Особенно мне понравилось, как вы объяснили свойства острого угла и его взаимосвязь с другими углами. Это действительно помогает лучше понять геометрию и использовать ее в повседневной жизни. Я обязательно поделюсь этой информацией с друзьями. Спасибо за познавательную статью!
Острый угол в математике — это угол, который меньше 90 градусов. Когда я впервые услышала об этом понятии, я задумалась о том, какие примеры острых углов можно встретить в реальной жизни. И вспомнилось, как я смотрела на закат солнца и видела, как его лучи падают под острым углом на поверхность земли. Также острые углы можно наблюдать в геометрии, например, в треугольнике, где все углы меньше 90 градусов. Интересно, что острые углы обладают рядом свойств, например, их сумма всегда составляет меньше 180 градусов. Все это делает понятие острого угла увлекательным и полезным в математике и в повседневной жизни.
Острый угол в математике — это угол между двумя лучами, которые пересекаются в одной точке и таким образом образуют угол меньше 90 градусов. Острый угол обычно ассоциируется с чем-то острым и означает, что угол открытый, маленький и острый, как острие иголки или кончик острия карандаша. Примеры острых углов в повседневной жизни встречаются повсюду: острый угол может быть углом двух стен в комнате, углом между лопатками ветряка или углом между двумя линиями на листе бумаги. Острые углы обладают рядом свойств: сумма всех углов треугольника равна 180 градусам, а в равнобедренном треугольнике острый угол равен углу между основанием и боковой стороной. Острый угол — это не просто понятие из математики, но и важный элемент повседневной жизни, который помогает нам разбираться в пространстве и геометрии окружающего нас мира.
Спасибо за интересную и познавательную статью! Я, как читатель, всегда стремлюсь расширить свои математические знания и ваша статья помогла мне лучше понять понятие острого угла. Было очень интересно узнать, что острый угол — это угол, который меньше 90 градусов. Примеры и иллюстрации, которые вы предоставили, помогли мне лучше представить, как острый угол выглядит на практике. Также, мне понравилось узнать о свойствах острых углов, таких как их сумма, равная 180 градусов, и то, что они могут быть использованы для решения различных задач. В целом, статья была легкой для понимания и информативной. Я надеюсь, что вы будете продолжать делиться своими знаниями и статьи с математическим содержанием. С нетерпением жду новых публикаций!