Что такое прямая по математике

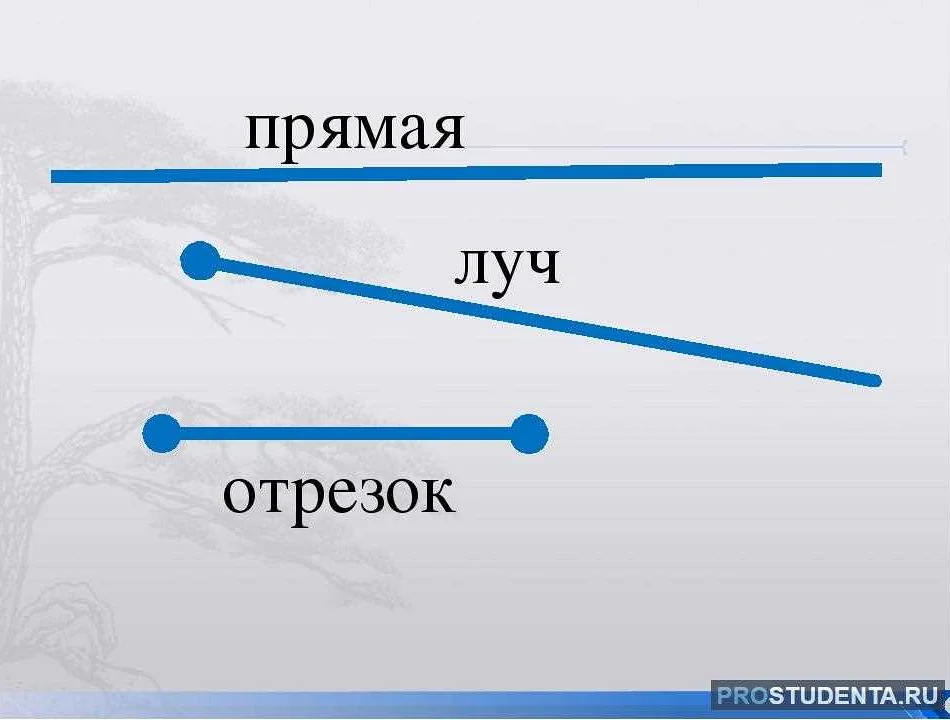
Прямая в математике — это геометрическая фигура, состоящая из бесконечного числа точек, которые лежат на одной линии. Прямая имеет нулевую ширину и бесконечную длину. Она является одним из основных объектов изучения в геометрии и алгебре, и широко используется в различных областях науки и техники.

Прямая – одно из основных понятий математики, которое играет важную роль в геометрии и алгебре. Она является одномерным геометрическим объектом без ширины и толщины. Прямая представляет собой бесконечную линию, которая состоит из бесконечного числа точек, расположенных в одном направлении.

Основное свойство прямой заключается в том, что любые две точки на ней можно соединить отрезком, причем этот отрезок будет полностью лежать на прямой. Также прямая не имеет начала и конца – она продолжается бесконечно в обе стороны. Это свойство позволяет применять прямые для построения графиков функций, решения уравнений и многих других математических задач.

Прямая играет важную роль в алгебре, геометрии и физике. В алгебре она используется для представления уравнений, графиков функций и анализа зависимостей между величинами. В геометрии прямая служит основой для построения различных фигур и определения их свойств. В физике прямая используется для моделирования движения и изменения различных физических величин.

Прямая имеет множество свойств и характеристик, которые изучаются в математике. Некоторые из них включают прямую линию, точку пересечения двух прямых, угол между двумя прямыми и т.д. Кроме того, прямая может быть горизонтальной, вертикальной или наклонной.

Изучение прямой является основой для понимания различных математических концепций и применения их на практике. Понимание определения и свойств прямой позволяет решать разнообразные задачи, анализировать данные и строить модели в различных областях науки и техники.

Прямая в математике: определение и свойства

Прямая может быть задана различными способами. Один из самых распространенных способов — это задать прямую с помощью уравнения. Например, уравнение прямой вида y = mx + b, где m — это наклон прямой, а b — это точка пересечения прямой с осью y.

У прямой есть несколько основных свойств:

1. Прямая не имеет начала и конца, она продолжается в обе стороны бесконечно.
2. Любые две точки на прямой можно соединить отрезком, который также будет лежать на прямой.
3. Прямая делит плоскость на две полуплоскости — верхнюю и нижнюю. Верхняя полуплоскость содержит все точки, лежащие выше прямой, а нижняя полуплоскость содержит все точки, лежащие ниже прямой.
4. Если две прямые пересекаются, то они пересекаются в одной точке. Если две прямые не пересекаются, то они либо параллельны, либо совпадают.
5. Прямая может быть параллельна координатным осям. В этом случае она будет иметь уравнение вида x = c, где c — это константа.

Прямые играют важную роль в геометрии и анализе. Они используются для изучения геометрических фигур, задач на построение, а также в физике и других науках.

Определение прямой в математике

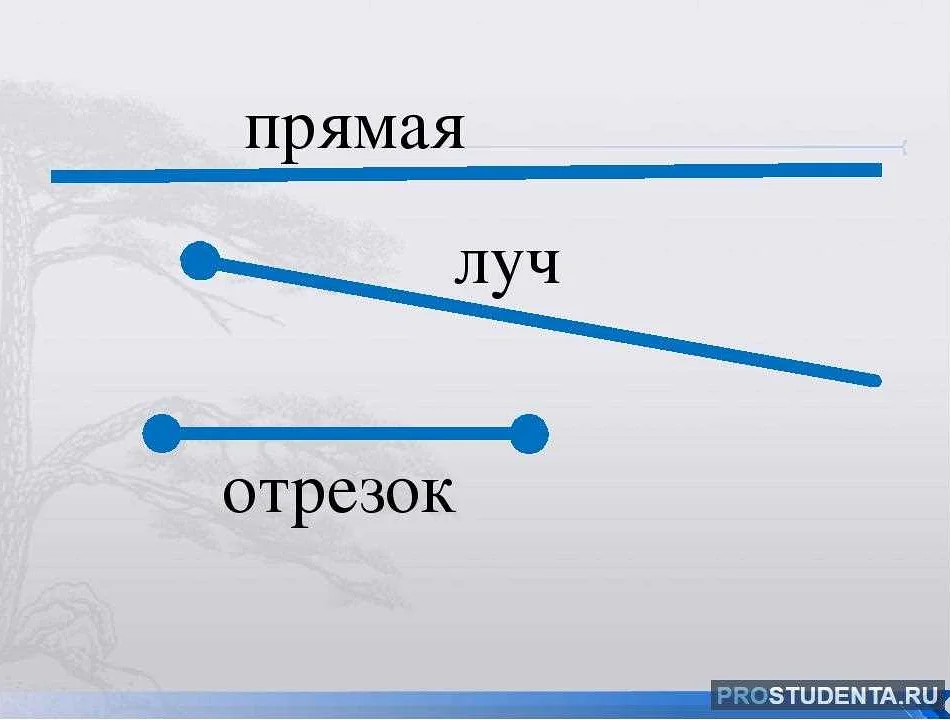
• Прямая не имеет начала и конца, она продолжается бесконечно в обе стороны.
• Любые две точки на прямой можно соединить отрезком, лежащим полностью на прямой.
• Любая точка в пространстве может быть однозначно определена с помощью координат на прямой.
• Прямая делит плоскость на две полуплоскости, называемые полупространствами.
• Прямая является кратчайшим пути между двумя точками.
• Прямая не имеет изгибов и кривизны, она всегда сохраняет прямолинейное направление.

Прямые могут быть заданы различными способами, например, с помощью уравнений, векторов или графиков. Они широко применяются в геометрии, физике, экономике и других научных дисциплинах для анализа и моделирования различных явлений и процессов.

Свойства прямой

1. Прямая является бесконечной в обе стороны. Это означает, что она не имеет начала и конца и простирается вдоль одной оси.
2. На прямой можно выбрать любые две точки. Это позволяет определить ее положение в пространстве и ориентацию.
3. Любые две точки на прямой можно соединить отрезком. Это позволяет измерить расстояние между ними и определить длину отрезка.
4. Прямая разделяет плоскость на две части — полуплоскости. Полуплоскости отличаются тем, что одна сторона прямой находится внутри, а другая — снаружи.
5. Если две прямые пересекаются, то они образуют углы. Углы могут быть острыми, прямыми или тупыми в зависимости от их величины.
6. Прямая может быть параллельна другой прямой. Параллельные прямые не пересекаются и лежат на одной плоскости.

Эти свойства прямой играют важную роль в геометрии и помогают в решении различных задач, связанных с пространством и фигурами.

Уравнение прямой

Коэффициент наклона k определяет угол наклона прямой относительно оси x. Если k положительный, то прямая наклонена вправо, если отрицательный – влево. Значение k определяется как отношение изменения значения y к изменению значения x на прямой.

Свободный член b определяет смещение прямой вверх или вниз относительно оси y. Если b положительный, то прямая смещена вверх, если отрицательный – вниз.

Уравнение прямой может быть представлено в различных формах, например, в общем виде Ax + By + C = 0, где A, B и C – это коэффициенты, либо в каноническом виде y = mx + c, где m – это коэффициент наклона, а c – это свободный член.

Виды прямых

В математике существует несколько видов прямых, которые имеют свои особенности и свойства.

1. Горизонтальная прямая: это прямая, которая лежит параллельно горизонтальной оси координат. Уравнение горизонтальной прямой имеет вид y = c, где с — постоянное значение.
2. Вертикальная прямая: это прямая, которая лежит параллельно вертикальной оси координат. Уравнение вертикальной прямой имеет вид x = c, где с — постоянное значение.
3. Наклонная прямая: это прямая, которая не параллельна ни горизонтальной, ни вертикальной осям координат. Уравнение наклонной прямой имеет вид y = mx + c, где m — коэффициент наклона и с — постоянное значение.

Это основные виды прямых, с которыми можно столкнуться в математике. Знание и понимание этих видов прямых помогает решать различные задачи и проблемы в области геометрии и аналитической геометрии.

Пересечение прямых

1. Если две прямые имеют общую точку, то они пересекаются в этой точке. Это называется точечным пересечением.
2. Если две прямые совпадают, то они пересекаются в любой точке, лежащей на данной прямой. Это называется полным пересечением.
3. Если две прямые параллельны, то они не пересекаются. В этом случае говорят, что прямые не имеют общих точек.

Пересечение прямых в математике имеет большое значение. Оно позволяет решать множество геометрических и алгебраических задач, таких как нахождение координат точки пересечения, определение условий параллельности или перпендикулярности прямых, построение графиков и многое другое.

Угол между прямыми

Для определения угла между прямыми используется угол между их направляющими векторами. Если у прямых заданы уравнения в общем виде Ax + By + C = 0, то их направляющие вектора имеют координаты (B, -A). Угол между прямыми определяется как угол между этими направляющими векторами.

Угол между прямыми может быть как острый (меньше 90 градусов), так и тупой (больше 90 градусов). Если угол между прямыми равен 90 градусов, то прямые называются перпендикулярными.

Свойства угла между прямыми:

• Угол между параллельными прямыми равен 0 градусов.
• Угол между перпендикулярными прямыми равен 90 градусам.
• Угол между скрещивающимися прямыми может быть любым значением от 0 до 180 градусов.
• Угол между прямыми, параллельными одной и той же плоскости, равен углу между нормалями к этой плоскости, проведенными из одной точки.

Знание угла между прямыми позволяет решать различные задачи, связанные с геометрией и аналитической геометрией, а также находить углы между прямыми в пространстве при помощи векторного произведения. Угол между прямыми является важным понятием для изучения геометрии и ее приложений в различных науках и инженерных областях.

Видео по теме:

Вопрос-ответ:

Что такое прямая в математике?

Прямая — это геометрическая фигура, состоящая из бесконечного множества точек, которые лежат на одной линии и не имеют изгибов или углов.

Как можно определить прямую?

Прямую можно определить как геометрическую фигуру, представляющую собой набор точек, которые могут быть описаны одним уравнением вида y = mx + b, где m — наклон прямой, b — точка пересечения с осью y.

Какие свойства имеет прямая?

Прямая обладает рядом свойств: она имеет равные углы с любой пересекающей ее прямой, она имеет равные углы между пересекающими ее прямыми, она имеет равные углы с параллельными ей прямыми и т.д.

Какие виды прямых выделяют в математике?

В математике выделяют несколько видов прямых: вертикальные (с наклоном 0), горизонтальные (с бесконечным наклоном), наклонные (с конечным наклоном), параллельные (никогда не пересекающиеся) и пересекающиеся.

Какие применения имеет прямая в реальной жизни?

Прямая имеет широкое применение в реальной жизни. Например, она используется в строительстве для прокладки дорог и зданий, в навигации для определения направления движения, в графике для отображения зависимости переменных, в физике для моделирования лучей света и т.д.

Что такое прямая в математике?

Прямая в математике — это геометрическое понятие, обозначающее бесконечную протяженность без изгибов и углов.

Как можно определить прямую?

Прямую можно определить различными способами. Например, прямая может быть определена как геометрическое место точек, лежащих на одной прямой линии. Также прямую можно задать с помощью уравнения, которое имеет вид y = kx + b, где k — коэффициент наклона, b — свободный член.

Расстояние от точки до прямой

Для вычисления расстояния от точки до прямой существует формула, которая основывается на использовании уравнения прямой и координат точки.

Пусть имеется прямая, заданная уравнением Ax + By + C = 0, и точка M(x0, y0), от которой необходимо найти расстояние до данной прямой. Тогда расстояние от точки M до прямой можно вычислить по формуле:

d = |Ax0 + By0 + C| / √(A2 + B2)

Здесь | | обозначает модуль числа, √ — корень квадратный.

Таким образом, зная коэффициенты A, B и C уравнения прямой, а также координаты точки M, можно легко вычислить расстояние от точки до прямой.

Расстояние от точки до прямой имеет важное применение в различных областях, таких как геометрия, физика, инженерия и других.

Прямая на плоскости и в пространстве

На плоскости прямую можно определить с помощью двух точек. Любые две различные точки на плоскости определяют прямую, проходящую через них. Прямая на плоскости также может быть задана уравнением вида y = kx + b, где k и b – константы, определяющие ее положение и направление.

В пространстве прямую можно определить с помощью трех точек. Любые три не коллинеарные точки в пространстве определяют прямую, проходящую через них. Прямая в пространстве также может быть задана параметрическими уравнениями, например, x = x0 + at, y = y0 + bt, z = z0 + ct, где x0, y0, z0 – координаты начальной точки прямой, а a, b, c – направляющие коэффициенты, определяющие ее направление.

Свойства прямой на плоскости и в пространстве являются основой для решения множества задач и применяются в различных областях науки и техники.