Что значит параллельно в математике

Понятие параллельности в математике означает, что две или более линии или объекта не пересекаются и всегда остаются на одном и том же расстоянии друг от друга. Узнайте подробности о параллельных линиях и фигурах в математике.

Параллельные линии – это одно из основных понятий в математике, которое важно для понимания геометрии и алгебры. Параллельные линии – это линии, которые лежат в одной плоскости и никогда не пересекаются, даже если продолжать их до бесконечности.

Определение параллельных линий включает в себя два основных условия. Во-первых, параллельные линии должны находиться в одной плоскости, то есть все точки каждой линии должны лежать на одной плоскости. Во-вторых, параллельные линии не должны пересекаться ни в одной точке. Если две линии удовлетворяют этим условиям, то они считаются параллельными.

Параллельные линии также имеют ряд свойств, которые помогают в решении различных задач и построении геометрических фигур. Например, параллельные линии имеют равные углы, образованные пересекающей их прямой. Они также имеют равные углы между секущей, пересекающей обе линии.

Параллельные линии широко применяются в различных областях науки и техники. Они используются для построения плоскостей, поиска решений в задачах оптимизации, а также для создания перспективных изображений в искусстве. Понимание свойств и определения параллельных линий помогает развивать логическое мышление и решать сложные математические задачи.

Параллельные линии: определение и свойства

Свойства параллельных линий:

1. Параллельные линии имеют одинаковый угол наклона. Это означает, что если одна линия наклонена под определенным углом к оси x, то все параллельные линии также будут наклонены под тем же углом.
2. Параллельные линии имеют одинаковое расстояние между собой на протяжении всей их длины. Это означает, что если расстояние между двумя параллельными линиями равно d, то расстояние между любыми другими параллельными линиями также будет равно d.
3. Параллельные линии не пересекаются ни в одной точке. Если две линии пересекаются, то они не могут быть параллельными.
4. Параллельные линии создают соответствующие углы, альтернативные углы и внутренние углы, которые имеют определенные свойства и отношения между собой.
5. Параллельные линии могут быть найдены и по другим свойствам, таким как равенство углов или параллельность соответствующих сторон в прямоугольных треугольниках и трапециях.

Знание свойств параллельных линий позволяет решать задачи, связанные с построением и измерением углов, расчетом расстояний и анализом геометрических фигур.

Видео по теме:

Что такое параллельные линии в математике?

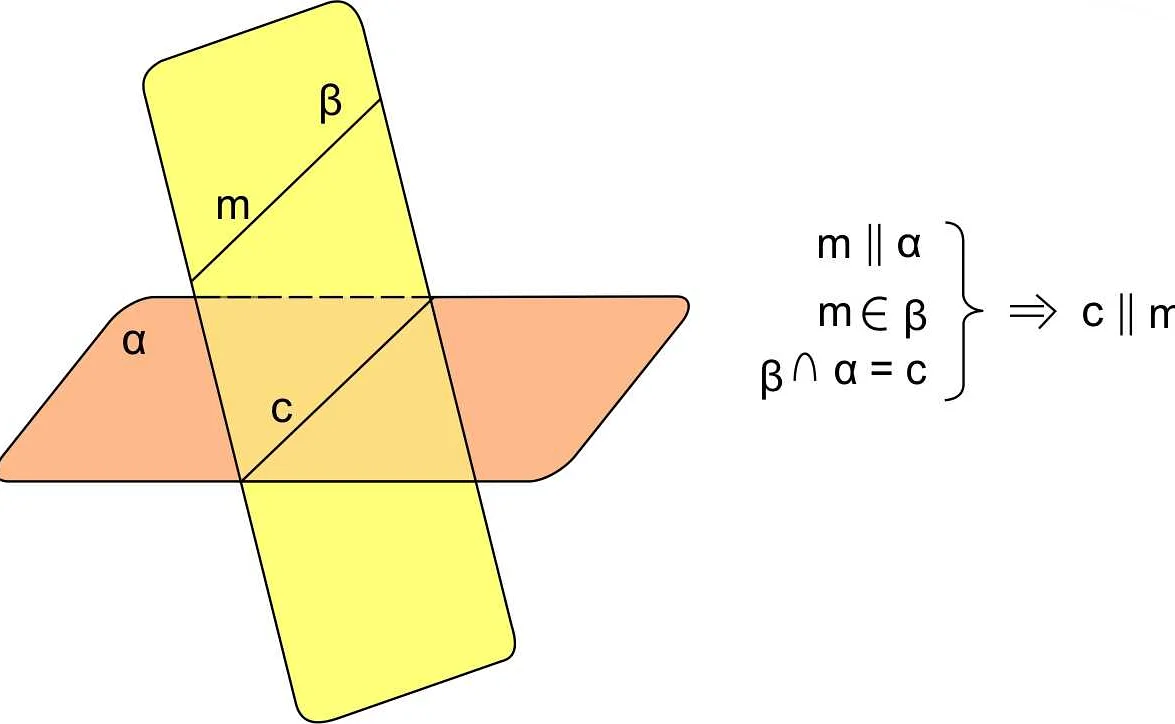
Два условия должны быть выполнены, чтобы линии были параллельными:

1. Линии должны лежать в одной плоскости.
2. Линии не должны пересекаться, то есть их расстояние должно оставаться неизменным на всей их протяженности.

Параллельные линии имеют несколько свойств:

• Они никогда не пересекаются.
• Углы между параллельными линиями равны или соответствующие друг другу.
• Если прямая пересекает одну из параллельных линий, то она пересекает и другую параллельную линию.
• Параллельные линии можно нарисовать с помощью параллельных переносов.

Параллельные линии широко применяются в геометрии и имеют важное значение в различных областях науки и техники.

Определение параллельных линий

Для того чтобы две линии считались параллельными, их направления должны быть одинаковыми и никогда не меняться. Например, если есть две вертикальные линии, то они считаются параллельными, так как обе направлены вверх и вниз. Если же имеются две горизонтальные линии, то они тоже параллельны, так как обе направлены слева направо или справа налево.

Параллельные линии имеют несколько свойств:

1. Расстояние между параллельными линиями постоянно и одинаково на всей их длине.
2. Углы между параллельными линиями равны друг другу и соответственны поперечным линиям, пересекающим параллельные линии.
3. Линии, которые пересекают одну параллельную линию, пересекают и другую параллельную линию при равных углах между пересекаемыми линиями.

Параллельные линии являются важным понятием в геометрии и широко используются не только в математике, но и во многих других областях, таких как архитектура, инженерия, картография и физика.

Свойства параллельных линий

1. Углы между параллельными линиями равны: Если две линии параллельны, то угол, образованный этими линиями и пересекающей их прямой, равен нулю.

2. Расстояние между параллельными линиями постоянно: Расстояние между двумя параллельными линиями всегда одинаково и не меняется по всей их длине.

3. Прямые, перпендикулярные к одной из параллельных линий, перпендикулярны и к другой: Если прямая перпендикулярна одной из параллельных линий, то она также перпендикулярна и ко второй линии.

4. Все параллельные линии расположены в одной плоскости: Все параллельные линии находятся в одной плоскости, которая не пересекается с другими плоскостями.

5. Параллельные линии не пересекаются: Параллельные линии могут быть продолжены в бесконечность, но они не пересекаются ни в одной точке.

6. Параллельные линии имеют одинаковый наклон: Если две линии параллельны, то их наклон или угол наклона будет одинаковым.

7. Альтернативные углы: При пересечении двух параллельных линий, альтернативные углы будут равными.

8. Параллельные линии имеют одинаковую ориентацию: Параллельные линии имеют одинаковую ориентацию, то есть они идут в одном и том же направлении.

9. Транзитивность параллельных линий: Если линия A параллельна линии B, и линия B параллельна линии C, то линия A также параллельна линии C.

10. Углы в смежных вершинах: Углы в смежных вершинах, образованные параллельными линиями и пересекающей их прямой, равны.

Соотношение углов между параллельными линиями

Соответственные углы образуются при пересечении двух параллельных линий с третьей линией, которая пересекает обе параллельные линии. Соответственные углы находятся на одном и том же месте относительно пересекающей линии и имеют одинаковую меру. Например, если две параллельные линии пересекаются третьей линией, то угол, образованный первой параллельной линией и пересекающей линией, будет равен углу, образованному второй параллельной линией и пересекающей линией.

Соответственные углы могут быть разных типов:

1. Вертикальные углы: два соответственных угла, которые находятся на противоположных сторонах пересекающей линии и образуются пересечением двух параллельных линий.
2. Углы-сиамские близнецы: два соответственных угла, которые находятся по одну сторону от пересекающей линии и образуются пересечением двух параллельных линий.
3. Внутренние и внешние углы: соответственные углы, которые находятся по разные стороны от пересекающей линии и образуются пересечением двух параллельных линий.

Соотношение углов между параллельными линиями является важным свойством, которое используется в различных задачах и доказательствах в геометрии. Оно позволяет делать выводы о равенстве и сравнении углов, основываясь на свойствах параллельных линий.

Пересечение параллельных линий

Параллельные линии не пересекаются, так как они имеют одинаковый наклон и расстояние между ними постоянно. Однако в геометрии существуют случаи, когда параллельные линии могут пересечься или соприкоснуться.

Пересечение параллельных линий может происходить в двух случаях:

1. Если линии находятся в трехмерном пространстве и пересекаются под углом. В этом случае они уже не являются просто параллельными.
2. Если одна из линий является перпендикуляром к другой параллельной линии. В этом случае перпендикуляр пересекает параллельные линии и образует углы в точках пересечения.

Кроме того, в геометрии также существуют специальные случаи пересечения параллельных линий, такие как пересечение параллельных линий бесконечно удаленной точкой или пересечение параллельных линий на бесконечности.

Пересечение параллельных линий является важным понятием в геометрии и находит применение в различных областях, включая архитектуру, инженерное дело и графику.

Координаты параллельных линий в пространстве

В двумерном пространстве параллельные линии можно определить как линии, которые никогда не пересекаются и имеют одинаковый угол наклона. Однако в трехмерном пространстве существует более сложное определение, так как наличие третьей координаты добавляет новые возможности.

Координаты параллельных линий в трехмерном пространстве определяются с использованием векторов. Для двух линий, параллельных друг другу, векторы направления этих линий должны быть коллинеарными, то есть лежать на одной прямой.

Координаты параллельных линий могут быть выражены с помощью уравнений прямых в пространстве. Уравнение прямой может быть записано в виде:

x = x₀ + at

y = y₀ + bt

z = z₀ + ct

Где x₀, y₀, z₀ — координаты точки, через которую проходит прямая, а a, b, c — компоненты вектора направления прямой. Параметр t может принимать любые значения.

Для параллельных линий уравнения прямых будут иметь одинаковые компоненты вектора направления a, b, c, но координаты точек x₀, y₀, z₀ могут быть разными.

Таким образом, чтобы определить параллельность двух линий в трехмерном пространстве, необходимо проверить коллинеарность их векторов направления, а также сравнить координаты точек, через которые проходят эти линии.

Примеры и приложения параллельных линий

Параллельные линии широко применяются в математике и в различных областях науки и техники. Ниже приведены некоторые примеры и приложения параллельных линий:

1. Геометрия:

В евклидовой геометрии параллельные линии играют важную роль. Они определяются как линии, которые лежат в одной плоскости и не пересекаются ни в одной точке. Это свойство параллельных линий используется для доказательства многих геометрических теорем и построений.

2. Архитектура:

В архитектуре параллельные линии используются для создания перспективных эффектов и визуального баланса. Здания и сооружения часто содержат параллельные линии, чтобы создать впечатление гармонии и симметрии.

3. Электротехника:

В электротехнике параллельные линии используются для создания электрических цепей. Параллельное соединение проводов позволяет увеличить сопротивление цепи и распределить ток равномерно.

4. Компьютерная графика:

В компьютерной графике параллельные линии используются для создания трехмерных моделей и визуализации объектов. Они помогают создать эффект глубины и перспективы в компьютерных изображениях.

5. Транспорт:

В дорожном строительстве параллельные линии используются для разметки дорог и пешеходных переходов. Они обеспечивают безопасность движения транспорта и пешеходов, а также помогают ориентироваться на дороге.

Это лишь некоторые примеры и приложения параллельных линий. В реальном мире мы часто сталкиваемся с параллельными линиями и используем их для решения различных задач и проблем.

Вопрос-ответ:

Что такое параллельные линии?

Параллельные линии — это линии, которые никогда не пересекаются в любой точке. Они лежат в одной плоскости и имеют одинаковое направление.

Как определить, что две линии параллельны?

Для определения параллельности линий можно использовать несколько способов. Один из самых простых — это проверка углов между ними. Если углы равны или их сумма равна 180 градусам, то линии параллельны. Также можно использовать параллельные линейки или провести перпендикуляры к обеим линиям и проверить их параллельность.

Какие свойства имеют параллельные линии?

У параллельных линий есть несколько важных свойств. Одно из них — если провести перпендикуляр к одной из параллельных линий, то он будет перпендикулярен и ко всем остальным линиям. Также, если провести перпендикуляр к одной из параллельных линий, то он будет параллелен другой линии. Кроме того, параллельные линии имеют одинаковое расстояние между собой на протяжении всей их длины.

Как параллельные линии используются в реальной жизни?

Параллельные линии находят широкое применение в различных областях, таких как архитектура, инженерия и графика. Например, при построении зданий и сооружений используются параллельные линии для создания правильных прямоугольных форм и симметричных конструкций. В графике и дизайне параллельные линии используются для создания перспективного вида и глубины в изображении. Также параллельные линии используются в геодезии и навигации для определения направления и расстояния между точками.