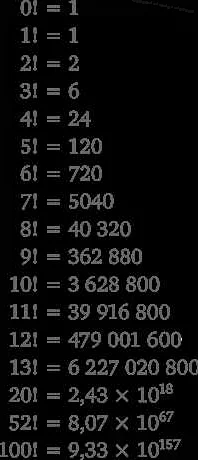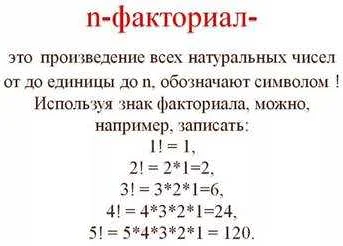Что такое перестановки в математике определение

Содержимое

1 Что такое перестановки в математике определение

Перестановки в математике — это упорядоченные наборы элементов, которые получаются путем перестановки их порядка. Узнайте, как определить и использовать перестановки в математике для решения различных задач.

Перестановка — это одна из основных операций в комбинаторике и математике в целом. Она представляет собой упорядоченное расположение элементов в различных комбинациях или порядках. В простых словах, перестановка — это способ размещения элементов в определенном порядке, который имеет значение и может быть описан числом.

Когда математики говорят о перестановках, они часто используют понятие факториала. Факториал — это произведение всех положительных целых чисел от 1 до заданного числа. Например, факториал числа 5 (обозначается как 5!) равен 5 х 4 х 3 х 2 х 1 = 120. Факториал используется для вычисления количества возможных перестановок элементов в заданной последовательности.

Примеры перестановок могут быть найдены во многих аспектах нашей жизни. Например, когда вы составляете список дел на день, вы создаете перестановку элементов, упорядочивая их в определенном порядке. Также перестановки играют важную роль в шифровании информации и различных алгоритмах.

Важно понимать, что порядок элементов имеет значение при перестановках. Это означает, что перестановка элементов «A, B, C» будет отличаться от перестановки элементов «C, B, A».

Перестановки — важный инструмент в математике и комбинаторике. Они помогают нам анализировать и понимать различные комбинации и порядки элементов. Понимание перестановок поможет в решении сложных задач и развитии логического мышления.

Перестановки в математике: определение и примеры

Перестановка представляет собой упорядоченный набор элементов, в котором каждый элемент используется ровно один раз. Другими словами, это способ переставить элементы так, чтобы каждый элемент занимал свою уникальную позицию.

Для определения числа перестановок из n элементов используется факториал. Факториал числа представляет собой произведение всех натуральных чисел от 1 до этого числа. Таким образом, число перестановок P из n элементов будет равно n!.

Например, пусть у нас есть множество из трех элементов: {A, B, C}. Всего возможно 3! = 3 * 2 * 1 = 6 перестановок:

Каждая перестановка представляет собой уникальную упорядоченную комбинацию элементов данного множества. Они широко применяются в различных областях математики, физики, информатики и других науках.

Что такое перестановки?

Для понимания перестановок можно рассмотреть простой пример. Пусть у нас есть множество из трех элементов: A, B и C. Тогда все возможные перестановки этого множества будут следующими:

Как видно из примера, порядок элементов в перестановке имеет значение. То есть, если поменять местами два элемента, получится другая перестановка.

Перестановки широко применяются в математике, комбинаторике, а также в других областях науки и техники. Они позволяют решать задачи по подсчету количества вариантов упорядоченных рассадок элементов и находить решения в различных задачах, связанных с комбинаторикой и теорией вероятностей.

Основные понятия перестановок

Основные понятия, связанные с перестановками:

Элементы перестановки	– это объекты или элементы, которые будут переставляться. Элементы могут быть числами, буквами, объектами или другими символами.
Длина перестановки	– это количество элементов в перестановке. Длина перестановки может быть любым натуральным числом.
Факториал	– это математическая функция, которая определяет количество всех возможных перестановок для заданной длины. Факториал обозначается символом «!» и вычисляется как произведение всех натуральных чисел от 1 до заданного числа включительно.
Порядок перестановки	– это количество элементов, которые находятся на своих местах после перестановки. Порядок перестановки может быть любым натуральным числом от 0 до длины перестановки.

Знание основных понятий перестановок позволяет лучше понять и решать различные задачи комбинаторики, а также применять перестановки в других областях математики и науки.

Формула для вычисления количества перестановок

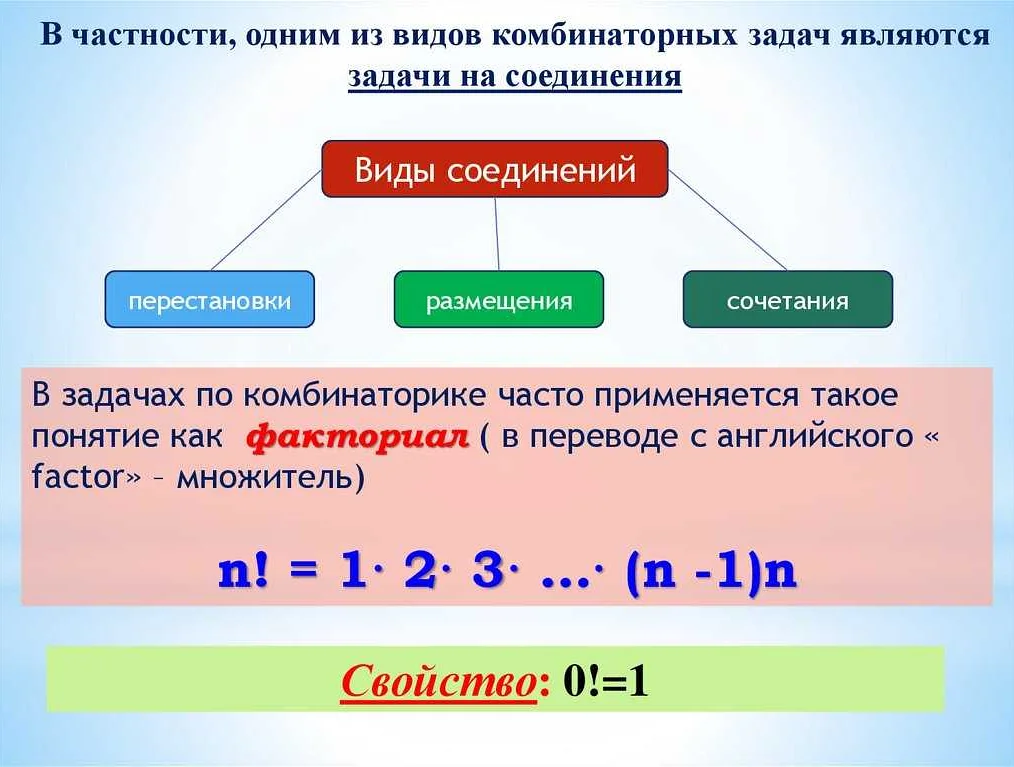
Количество перестановок из n элементов можно вычислить с помощью формулы:

P(n) = n!

где n! обозначает факториал числа n.

Факториал числа n равен произведению всех натуральных чисел от 1 до n.

Например, для n = 3, количество перестановок будет равно:

P(3) = 3! = 3 * 2 * 1 = 6

Таким образом, существует 6 различных перестановок из 3 элементов.

Как определить количество перестановок?

Количество перестановок можно определить с помощью формулы для расчета факториала. Факториал числа обозначается символом «!» и равен произведению всех натуральных чисел от 1 до этого числа.

Для определения количества перестановок из n элементов можно использовать следующую формулу:

n! = n × (n-1) × (n-2) × … × 2 × 1

Например, если у нас есть 5 элементов, то количество перестановок будет равно:

5! = 5 × 4 × 3 × 2 × 1 = 120

То есть, из 5 элементов можно составить 120 различных перестановок.

Примеры перестановок в математике

Пример 1: Пусть есть множество из трех элементов: {a, b, c}. Всего можно составить 3! = 3 * 2 * 1 = 6 перестановок:

abc, acb, bac, bca, cab, cba.

Пример 2: Рассмотрим множество из четырех элементов: {1, 2, 3, 4}. Количество перестановок равно 4! = 4 * 3 * 2 * 1 = 24:

1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321.

Пример 3: Возьмем множество из двух элементов: {x, y}. Всего можно составить 2! = 2 * 1 = 2 перестановки:

xy, yx.

Таким образом, перестановки используются для определения количества возможных упорядоченных комбинаций элементов множества.

Перестановки в комбинаторике

Факториал числа n, обозначается как n!, определяется как произведение всех положительных целых чисел от 1 до n.

Например, для множества {1, 2, 3} существуют 6 перестановок: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). В данном случае количество элементов равно 3, и его факториал равен 3! = 3 * 2 * 1 = 6.

Перестановки широко используются в различных областях математики, физики, информатики и других науках. Они позволяют решать задачи, связанные с упорядочиванием элементов и определением количества возможных вариантов.

Также перестановки являются основой для других комбинаторных понятий, таких как размещения и сочетания.

В таблице ниже приведены некоторые примеры перестановок для различных множеств:

МножествоКоличество элементовКоличество перестановок

{a, b}	2	2
{a, b, c}	3	6
{1, 2, 3, 4}	4	24
{x, y, z, w, v}	5	120

Практическое применение перестановок

Перестановки широко применяются в различных областях математики, науки и повседневной жизни. Вот несколько примеров их практического использования:

1. Комбинаторика: Перестановки часто используются для решения задач комбинаторики, таких как нахождение числа способов размещения объектов или составление различных комбинаций.

2. Криптография: В криптографии, перестановки могут использоваться для шифрования и дешифрования информации. Например, шифр перестановки меняет порядок символов в сообщении, делая его неразборчивым для посторонних.

3. Музыкальный анализ: В музыкальном анализе перестановки могут использоваться для анализа мелодических и ритмических структур в музыке. Они могут помочь выявить повторяющиеся фразы или мотивы.

4. Программирование: В программировании перестановки могут использоваться для решения задач ранжирования, сортировки и оптимизации. Алгоритмы перестановок помогают упорядочить данные по определенным критериям.

5. Игры: В некоторых играх, таких как головоломки и головоломки с числами, перестановки используются для создания различных комбинаций и нахождения решения.

Таким образом, перестановки играют важную роль в различных областях и имеют множество практических применений.

Вопрос-ответ:

Что такое перестановки в математике?

Перестановки в математике — это упорядоченные комбинации элементов, в которых порядок элементов имеет значение. В перестановках каждый элемент должен быть использован ровно один раз, и все элементы должны быть учтены.

Какая формула используется для вычисления количества перестановок?

Формула для вычисления количества перестановок из n элементов равна n!, где n — количество элементов. Факториал (обозначается !) означает произведение всех натуральных чисел от 1 до n.

Какие примеры перестановок можно привести?

Примеры перестановок можно привести для различных наборов элементов. Например, для набора из трех элементов {1, 2, 3} можно получить следующие перестановки: {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}.

Каково значение факториала для небольших чисел?

Значение факториала для небольших чисел можно легко вычислить. Например, факториал 0 равен 1, факториал 1 равен 1, факториал 2 равен 2, факториал 3 равен 6, факториал 4 равен 24 и т.д.

Каково максимальное количество перестановок из n элементов?

Максимальное количество перестановок из n элементов равно n!. Например, для набора из 4 элементов будет существовать 4! = 24 перестановки.

Что такое перестановки в математике: определение и примеры