Что такое перпендикулярно в математике

Понятие перпендикулярности в математике, описание свойств и применение перпендикулярных линий и плоскостей. Как определить перпендикулярные отрезки и углы.

Перпендикуляр — одно из основных понятий в математике, которое находит широкое применение в геометрии. В своем простом определении, перпендикуляр — это прямая линия, которая образует угол в 90 градусов с другой линией или плоскостью. Угол между перпендикулярными линиями называется прямым углом.

Одно из основных свойств перпендикуляров — то, что они пересекаются. Если две линии перпендикулярны друг другу, то они обязательно пересекаются и образуют прямые углы в точке пересечения. Это свойство позволяет использовать перпендикуляры в решении различных задач, например, в построении прямоугольных треугольников или нахождении высоты в треугольнике.

Еще одно важное свойство перпендикуляров — то, что они имеют противоположные наклоны. Если одна линия имеет положительный наклон, то перпендикуляр к ней будет иметь отрицательный наклон и наоборот. Это свойство позволяет использовать перпендикуляры в построении графиков функций и в решении задач на прямые.

Важно отметить, что перпендикулярность — это не только геометрическое понятие, но и алгебраическое. В алгебре перпендикулярные прямые характеризуются своими угловыми коэффициентами. Если у двух прямых угловой коэффициент одинаковый, но с противоположными знаками, то эти прямые будут перпендикулярными. Это позволяет находить перпендикулярные прямые по их аналитическим уравнениям.

Определение перпендикуляра в математике

Для определения перпендикуляра важно учесть две основные характеристики:

1. Перпендикулярные линии должны быть прямыми.
2. Угол между перпендикулярными линиями должен составлять 90 градусов.

Перпендикуляр используется в различных областях математики и геометрии. Например, в прямоугольной системе координат перпендикулярные линии часто используются для обозначения осей координат — x и y.

Также перпендикулярные линии встречаются при изучении треугольников и других геометрических фигур. Углы, образованные перпендикулярными линиями, могут использоваться для решения задач, например, для определения высоты или нахождения площади фигуры.

Важно отметить, что перпендикулярность — это свойство отношения между двумя линиями. Линия может быть перпендикулярной к другой, но не иметь перпендикулярных линий внутри себя.

Все перпендикулярные линии могут быть представлены в виде таблицы, где каждая строка представляет собой пару перпендикулярных линий.

Линия 1Линия 2

AB	CD
EF	GH
IJ	KL

Как найти перпендикуляр к прямой или отрезку

Чтобы найти перпендикуляр к прямой или отрезку, необходимо знать его свойства и использовать определенные методы.

Для начала, давайте определимся с терминами. Перпендикуляр — это линия, которая образует прямой угол (угол в 90 градусов) с другой линией. Перпендикуляр к прямой или отрезку проходит через его середину и делит его на две равные части.

Есть несколько способов найти перпендикуляр:

СпособОписание

1. Использование углов	Если вам дана прямая или отрезок, вы можете найти его перпендикуляр, построив прямой угол с помощью транспортира или другого измерительного инструмента. Затем проведите линию через середину прямого угла, чтобы получить перпендикуляр.
2. Использование перпендикулярных линий	Если у вас уже есть другая перпендикулярная линия, вы можете использовать ее для построения нового перпендикуляра. Продлите перпендикулярную линию через середину прямого угла, чтобы получить новый перпендикуляр.
3. Использование формулы	Если вам известны координаты точек на прямой или отрезке, вы можете использовать формулу для нахождения перпендикуляра. Формула зависит от типа прямой или отрезка (наклонной или вертикальной).

Все эти способы могут быть использованы для нахождения перпендикуляра к прямой или отрезку в математике. Выберите тот, который наиболее удобен для вас и применяйте его в соответствующих случаях.

Уравнение перпендикуляра в прямоугольной системе координат

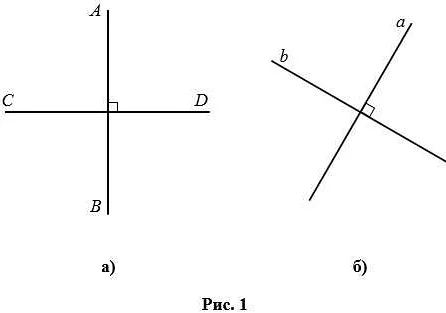
Уравнение перпендикуляра в прямоугольной системе координат может быть определено с помощью двух основных элементов: точки, через которую проходит перпендикуляр, и наклона этого перпендикуляра.

Для нахождения уравнения перпендикуляра, нужно знать координаты точки, через которую он проходит. Обозначим эту точку через P(x1, y1).

Также необходимо знать наклон перпендикуляра, то есть его угловой коэффициент k. Угловой коэффициент можно найти с помощью формулы k1 = -1/k, где k1 — угловой коэффициент перпендикуляра.

Таким образом, уравнение перпендикуляра в прямоугольной системе координат имеет вид y — y1 = k1(x — x1).

Это уравнение можно переписать и в общем виде: y = k1x — k1x1 + y1.

При решении задачи нахождения уравнения перпендикуляра важно помнить, что наклон перпендикуляра будет отличаться от наклона исходной прямой. Перпендикуляр к горизонтальной прямой будет вертикальной, а перпендикуляр к вертикальной прямой будет горизонтальной.

Свойства перпендикуляров

Перпендикулярные прямые имеют несколько основных свойств:

1. Перпендикулярные прямые образуют прямой угол между собой. Это означает, что угол между перпендикулярами равен 90 градусам.
2. Если две прямые перпендикулярны к одной третьей прямой, то они параллельны друг другу. Это свойство называется перпендикулярной теоремой.
3. Если к прямой провести перпендикуляр, то он будет касаться этой прямой в точке пересечения.
4. Если две прямые перпендикулярны к одной плоскости, они будут параллельны друг другу.
5. Если на плоскости задана точка и прямая, проходящая через эту точку перпендикулярно плоскости, то все прямые, перпендикулярные этой прямой, будут лежать в плоскости.
6. Если два отрезка перпендикулярны друг другу, то их длины удовлетворяют теореме Пифагора: сумма квадратов длин этих отрезков равна квадрату длины гипотенузы.

Перпендикулярные прямые и отрезки

Основное свойство перпендикулярных прямых и отрезков состоит в том, что угол между ними равен 90 градусам. Это означает, что если две прямые или отрезка пересекаются под прямым углом, то они являются перпендикулярными.

Перпендикулярные отрезки могут быть использованы для построения прямоугольника или квадрата. В прямоугольнике все углы равны 90 градусам, а стороны прямоугольника являются перпендикулярными.

Перпендикулярные прямые играют важную роль в геометрии, а также в других областях математики, таких как тригонометрия и алгебра. Они используются для решения различных задач и построения геометрических фигур.

Важно помнить, что перпендикулярные прямые или отрезки всегда пересекаются под прямым углом, и угол между ними равен 90 градусам. Это свойство помогает решать множество задач и делает перпендикулярные линии важными элементами в геометрии и математике в целом.

Видео по теме:

Вопрос-ответ:

Что такое перпендикуляр в математике?

Перпендикуляр — это геометрическая линия, которая пересекает другую линию или плоскость в прямом угле, то есть под углом 90 градусов.

Как определить, являются ли две линии перпендикулярными?

Две линии считаются перпендикулярными, если угол, который они образуют на их пересечении, равен 90 градусов. Если угол равен 90 градусов, то линии перпендикулярны, в противном случае они не перпендикулярны.

Какое значение имеет перпендикуляр в геометрии?

Перпендикуляр — это важное понятие в геометрии, которое используется для построения прямых углов, определения прямых исходя из заданных условий, а также в решении различных задач и построении геометрических фигур.

Какие свойства имеет перпендикуляр?

Перпендикуляр обладает несколькими основными свойствами. Во-первых, перпендикулярные линии пересекаются в прямом углу. Во-вторых, если две линии перпендикулярны к одной и той же линии, то они параллельны между собой. В-третьих, перпендикуляр делит отрезок, на котором лежит, на две равные части.

Перпендикулярные плоскости в трехмерном пространстве

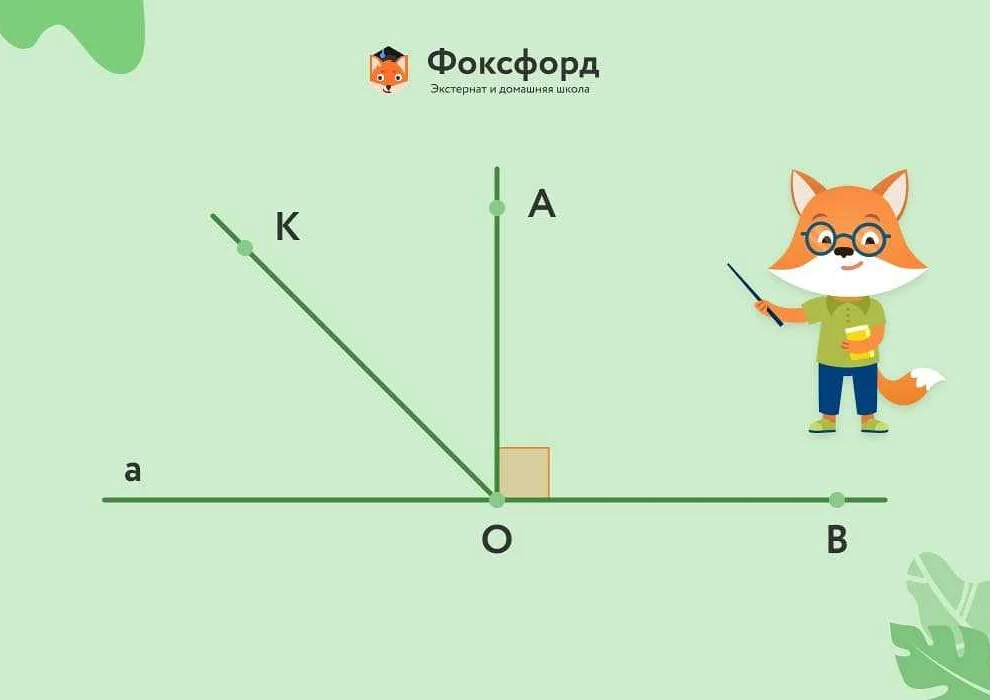
Для определения перпендикулярности двух плоскостей необходимо проверить, что их нормальные векторы ортогональны друг другу. Нормальный вектор плоскости – это вектор, перпендикулярный этой плоскости и указывающий в направлении, обратном к нормали.

Для проверки перпендикулярности плоскостей, можно воспользоваться скалярным произведением их нормальных векторов. Если скалярное произведение равно нулю, то плоскости перпендикулярны.

Условие перпендикулярности плоскостейСкалярное произведение нормальных векторов

Две плоскости перпендикулярны

n1 · n2 = 0

Если плоскости заданы уравнениями вида ax + by + cz + d1 = 0 и ax + by + cz + d2 = 0, то их нормальные векторы можно найти, взяв коэффициенты перед x, y и z. Таким образом, нормальный вектор первой плоскости будет равен n1 = (a, b, c), а нормальный вектор второй плоскости будет равен n2 = (a, b, c).

Зная уравнения плоскостей и их нормальные векторы, можно проверить перпендикулярность плоскостей, используя скалярное произведение. Если скалярное произведение нормальных векторов равно нулю, то плоскости перпендикулярны.

Примеры использования перпендикуляра в задачах

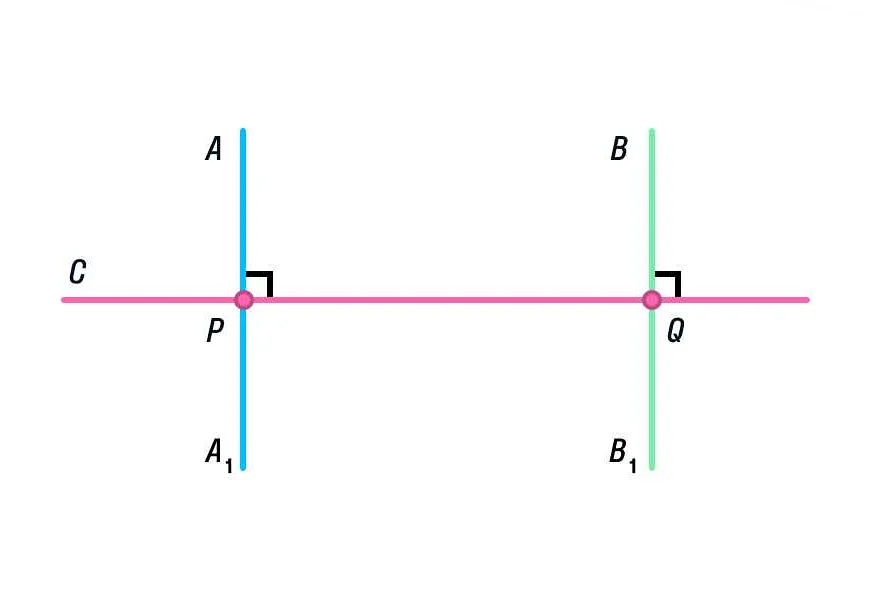
Перпендикуляры широко применяются в математике для решения различных задач. Рассмотрим несколько примеров использования перпендикуляра:

1. Построение перпендикуляра к прямой:

Дана прямая AB и точка C, которая не лежит на этой прямой. Необходимо построить перпендикуляр к прямой AB, проходящий через точку C. Для этого можно воспользоваться следующим алгоритмом:

1. Соединить точки A и B линией.
2. На линии AB отметить точку D.
3. Соединить точки C и D линией.
4. Линия CD будет перпендикуляром к прямой AB.

2. Определение перпендикулярности:

Даны две прямые AB и CD. Необходимо определить, являются ли они перпендикулярными. Для этого можно использовать теорему о перпендикулярности, которая утверждает, что две прямые перпендикулярны, если их угловой коэффициент произведения равен -1. То есть, если угловой коэффициент прямой AB равен k1, а угловой коэффициент прямой CD равен k2, то условие перпендикулярности будет выполняться, если k1 * k2 = -1.

3. Поиск высоты треугольника:

Дан треугольник ABC. Необходимо найти высоту треугольника, проведенную из вершины A. Высота треугольника является перпендикуляром, проведенным из вершины к противоположному основанию. Для нахождения высоты можно использовать теорему о перпендикуляре к основанию, которая утверждает, что высота треугольника перпендикулярна основанию и проходит через середину этого основания.

Таким образом, перпендикуляры являются важным инструментом для решения различных задач в математике и находят применение в геометрии, алгебре и других областях.