Что такое прямые линии в математике

Прямые линии — это основной элемент геометрии, представляющий собой бесконечно протяженную идеально прямую. Они имеют постоянное направление и не имеют изгибов или изгибов. Прямые линии играют важную роль в математике, а их свойства и применения широко изучаются в различных областях науки и техники.

Прямые линии являются одним из основных понятий в математике. Они представляют собой геометрические объекты, которые не имеют ни начала, ни конца, и простираются в бесконечность в обе стороны. Прямые линии имеют множество свойств и применяются в различных областях математики и физики.

Определение прямой линии в математике довольно простое. Прямая линия – это множество всех точек, которые лежат на одной прямой и не принадлежат ни одной другой линии. Прямые линии не имеют ширины и представляют собой простые одномерные геометрические объекты.

Прямые линии обладают рядом важных свойств, которые позволяют решать различные задачи в математике и физике. Одно из таких свойств – прямая линия является кратчайшим расстоянием между двумя точками. Более того, прямая линия обладает симметрией относительно любой ее точки, а также может быть продолжена в бесконечность в обе стороны.

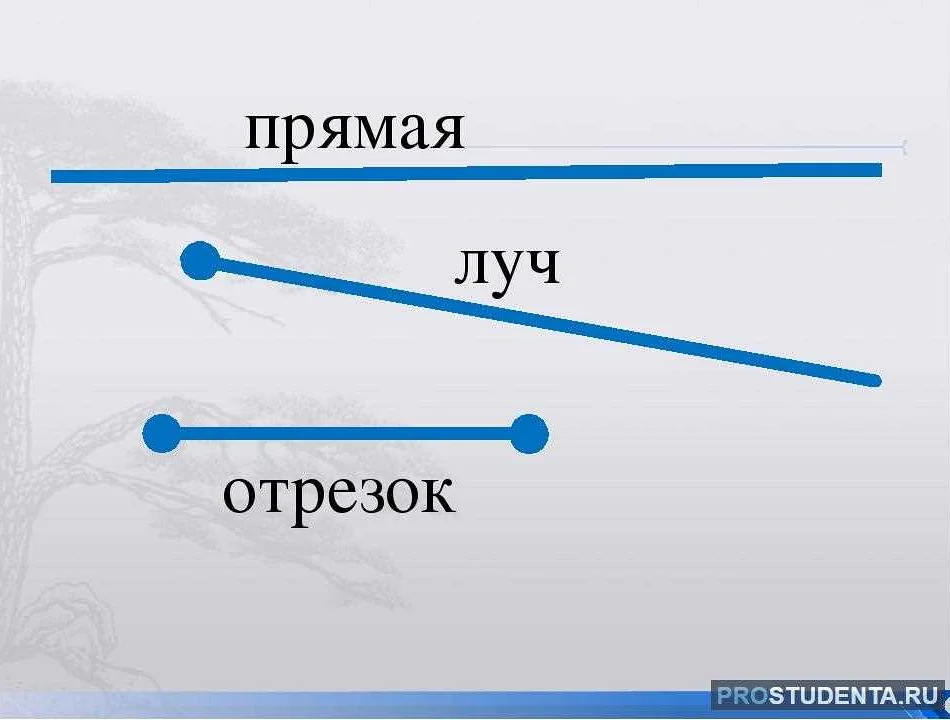
Прямые линии применяются во многих областях математики, включая геометрию, анализ и алгебру. Они используются для решения задач геометрии, построения графиков функций, а также для описания и анализа пространственных объектов и фигур. Примерами прямых линий могут служить отрезки, отрезки прямых, лучи и прямые на плоскости, а также прямые в трехмерном пространстве.

Определение прямой линии

Прямая линия является одним из основных понятий в геометрии и может быть определена как наименьшее расстояние между двумя точками. Любые две точки на прямой линии можно соединить отрезком прямой, который будет полностью лежать на этой линии.

Прямая линия также имеет свойства, которые отличают ее от других линий. Например, она не имеет изгибов или изломов и может быть описана уравнением вида y = kx + b, где k и b — константы.

Прямые линии используются во многих областях математики, физики и инженерии. Они помогают в решении задач, связанных с движением, графиками функций, анализом данных и многими другими.

Видео по теме:

Свойства прямых линий

У прямой линии есть несколько важных свойств:

1.	Прямая линия является кратчайшим расстоянием между двумя точками. Если две точки A и B лежат на прямой, то расстояние между ними будет наименьшим по сравнению с расстояниями по другим путям.
2.	Прямая линия разделяет плоскость на две части — полуплоскости. Все точки, лежащие по одну сторону от прямой, принадлежат одной полуплоскости, а все точки, лежащие по другую сторону от прямой, принадлежат другой полуплоскости.
3.	Прямая линия имеет нулевую ширину, то есть ее ширина равна нулю. Прямая линия — это только одномерный объект, который не имеет площади.
4.	Прямая линия может быть описана уравнением вида y = mx + b, где m — коэффициент наклона прямой, а b — коэффициент сдвига по оси y (y-пересечение).
5.	Прямая линия может быть горизонтальной, если ее уравнение имеет вид y = c, где c — постоянная величина. В этом случае прямая параллельна оси x.
6.	Прямая линия может быть вертикальной, если ее уравнение имеет вид x = d, где d — постоянная величина. В этом случае прямая параллельна оси y.

Это лишь некоторые из свойств прямых линий, которые помогают нам понять и использовать их в математике и геометрии.

Уравнение прямой линии

Общий вид уравнения прямой линии в декартовой системе координат имеет вид:

y = mx + b

Здесь m – коэффициент наклона прямой, который определяет угол, под которым прямая пересекает ось x, и b – свободный член, который определяет смещение прямой относительно оси y.

Уравнение прямой можно представить также в виде:

ax + by + c = 0

Здесь a, b и c – коэффициенты, которые также определяют свойства прямой.

Зная уравнение прямой, можно определить её свойства, такие как наклон, пересечение с осями координат, искать точку пересечения с другой прямой и многое другое.

Примеры уравнений прямой:

1. y = 2x + 3 – прямая с коэффициентом наклона 2 и свободным членом 3.

2. 2x — y = 5 – прямая с коэффициентами a = 2, b = -1 и c = -5.

3. x = 4 – вертикальная прямая, которая пересекает ось x в точке 4.

Вопрос-ответ:

Что такое прямая линия в математике?

Прямая линия в математике — это геометрическая фигура, которая не имеет ни начала, ни конца, и простирается в бесконечность в обе стороны.

Какие свойства имеют прямые линии?

Прямые линии имеют несколько основных свойств. Во-первых, любые две точки на прямой линии можно соединить отрезком, который будет лежать полностью на этой линии. Во-вторых, прямая линия делит плоскость на две полуплоскости. В-третьих, прямая линия может быть описана с помощью уравнения вида y = kx + b, где k — коэффициент наклона, b — коэффициент смещения.

Можете ли вы привести примеры прямых линий в реальной жизни?

Конечно! Прямые линии можно встретить в разных сферах жизни. Например, провода на электрической линии, балки на строительном объекте, железнодорожные пути, границы дороги, радиусы окружностей и т.д.

Какие методы можно использовать для построения прямой линии?

Существует несколько методов для построения прямой линии. Один из них — использование двух точек на плоскости и соединение их отрезком. Другой метод — использование уравнения прямой для определения координат точек, через которые прямая должна проходить. Дополнительно можно использовать линейку или другие инструменты, чтобы обеспечить более точное построение.

Перпендикулярные прямые линии

Свойства перпендикулярных прямых:

• Угол между перпендикулярными прямыми всегда равен 90 градусов.
• Перпендикулярные прямые имеют противоположные угловые коэффициенты.
• Уравнение перпендикулярной прямой может быть получено путем изменения знаков коэффициентов уравнения и изменения их местами.
• Перпендикулярные прямые не пересекаются и не параллельны.

Примеры перпендикулярных прямых:

1. Вертикальная и горизонтальная прямые на координатной плоскости.
2. Диагонали квадрата.
3. Высота и основание прямоугольника.

Знание свойств и примеров перпендикулярных прямых помогает решать задачи в геометрии и аналитической геометрии, а также применять их в реальных ситуациях, например, при построении зданий или дорог.

Параллельные прямые линии

Для того чтобы две линии были параллельными, их направления должны быть одинаковыми. Это означает, что угол между ними должен быть равен нулю или 180 градусов.

Параллельные прямые линии имеют несколько свойств:

• Свойство 1: Две параллельные линии никогда не пересекаются. Если они пересекаются, то они не являются параллельными.
• Свойство 2: Расстояние между параллельными линиями всегда постоянное и не меняется ни при каких условиях.
• Свойство 3: Линия, перпендикулярная одной из параллельных линий, также перпендикулярна и другой параллельной линии.

Примеры параллельных прямых линий могут быть найдены в различных геометрических фигурах, таких как параллелограммы, прямоугольники и треугольники.

Понимание параллельных прямых линий является важным основополагающим элементом в геометрии и находит свое применение в различных областях, таких как инженерия, архитектура и физика.

Расстояние между двумя точками на прямой линии

Расстояние = |xB — xA|

где xA и xB — координаты точек A и B соответственно.

Например, если точка A имеет координату -3, а точка B — 5, то расстояние между ними будет:

Расстояние = |-5 — (-3)| = |-5 + 3| = |-2| = 2

Таким образом, расстояние между точками A и B на прямой линии равно 2.

Это свойство расстояния между точками на прямой линии позволяет нам определить длину отрезка и измерить расстояние между любыми двумя точками на прямой.

Примеры прямых линий в реальной жизни

1. Дороги и трассы: Множество дорог и трасс, которые мы видим ежедневно, представляют собой прямые линии. Они могут быть прямыми отрезками или состоять из нескольких прямых участков, но в целом они следуют прямолинейному пути.

2. Железнодорожные пути: Железнодорожные пути также представляют собой прямые линии. Они создаются для обеспечения эффективного и безопасного движения поездов между городами и населенными пунктами.

3. Здания и строения: Множество зданий и строений имеют прямые линии в своей архитектуре. Например, стены, окна, двери, потолки и полы могут быть прямолинейными.

4. Электрические провода и линии передачи: Линии электроснабжения и передачи электроэнергии часто представляют собой прямые линии, чтобы обеспечить эффективную передачу энергии от источника к потребителю.

5. Построение и строительство: При строительстве и постройке часто используются прямые линии для обеспечения точности и симметрии. Например, при установке фундамента, стен или декоративных элементов.

6. Геометрические инструменты: Множество геометрических инструментов, таких как линейка, штангенциркуль или уровень, имеют прямые линии в своем дизайне и используются для измерения или создания прямых линий.

Это лишь некоторые примеры, которые иллюстрируют использование прямых линий в реальной жизни. Прямые линии играют важную роль в различных областях, от инженерии и архитектуры до геометрии и дизайна.