Что такое плоскость в математике простыми словами

Плоскость в математике – это двумерное геометрическое пространство, состоящее из точек, лежащих на одной плоскости. Эта концепция играет важную роль в различных областях математики и физики, позволяя нам изучать и моделировать различные объекты и явления. Понимание плоскости помогает решать задачи и строить графики, а также имеет практическое применение в архитектуре, инженерии и других сферах нашей жизни.

Плоскость — это понятие, которое широко используется в математике. Плоскость можно представить как бесконечно большую и ровную поверхность, которая не имеет ни высоты, ни ширины. Она состоит из неограниченного количества точек и не имеет краев или границ.

Математики используют плоскость для изучения геометрии и решения различных задач. В геометрии, плоскость выступает в качестве основы для построения геометрических фигур и проведения прямых и кривых линий.

Один из основных принципов плоскости — это то, что две точки определяют прямую, три точки определяют плоскость, а четыре точки, не лежащие в одной плоскости, определяют пространство.

Плоскость можно представить, например, как поверхность стола или листа бумаги. Она имеет длину и ширину, но не имеет толщины. В математике, плоскость абстрактна и не ограничена размерами, она существует как идея и инструмент для изучения мира вокруг нас.

Изучение плоскости в математике позволяет нам понять и анализировать различные геометрические фигуры и применять полученные знания в решении задач разного типа. Понимание плоскости является фундаментальным для изучения более сложных математических концепций и теорий.

Что такое плоскость в математике?

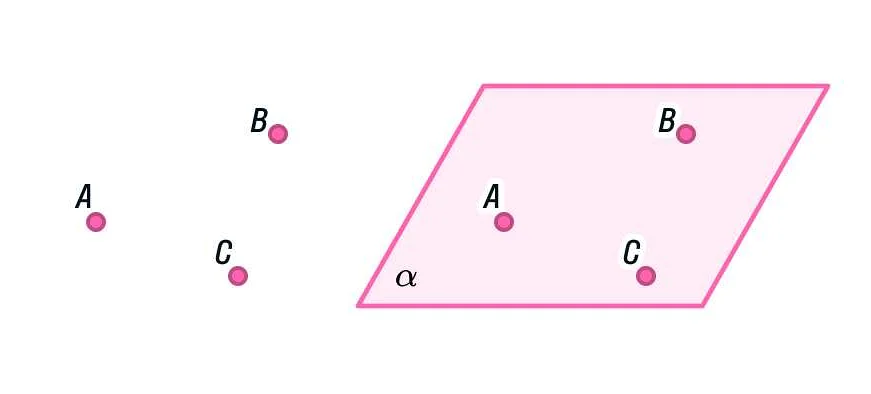
Плоскость можно представить себе как уровень или поверхность без высоты или глубины. Она не имеет толщины и не ограничена в каком-либо направлении. Вместо этого, плоскость простирается бесконечно во всех направлениях.

В математике плоскость обычно обозначается символом «π» или буквой «P». Плоскость может быть определена с помощью трех точек или с помощью уравнения, которое описывает ее положение в трехмерном пространстве.

Например, плоскость может быть определена с помощью трех точек A, B и C. Когда эти три точки не лежат на одной прямой, они определяют плоскость, которая проходит через них.

Плоскость является основным понятием в геометрии, а также используется в других областях математики и физики. Она широко применяется для описания и изучения различных геометрических фигур, от прямоугольников и треугольников до кругов и эллипсов.

Видео по теме:

Определение и основные характеристики

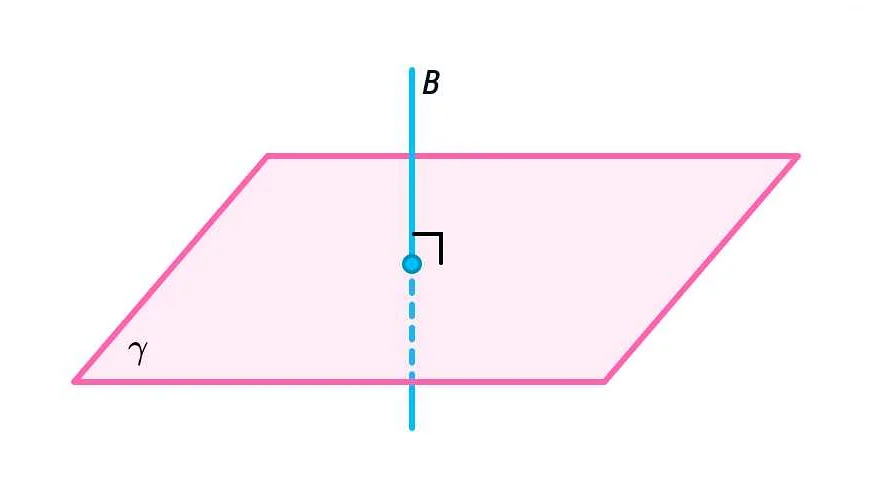
Основные характеристики плоскости:

1. Прямые линии: плоскость содержит бесконечное количество прямых линий, которые могут быть параллельными, пересекать друг друга или быть взаимно перпендикулярными.
2. Углы: плоскость также содержит бесконечное количество углов, образованных пересечением двух прямых линий.
3. Фигуры: на плоскости можно строить различные геометрические фигуры, такие как треугольники, квадраты, круги и многое другое.
4. Расстояния: на плоскости можно измерить расстояние между двумя точками, используя прямую линию, которая соединяет эти точки.

Плоскость является важным понятием в математике и широко применяется в различных областях, включая геометрию, алгебру, физику и инженерное дело.

Геометрическое представление плоскости

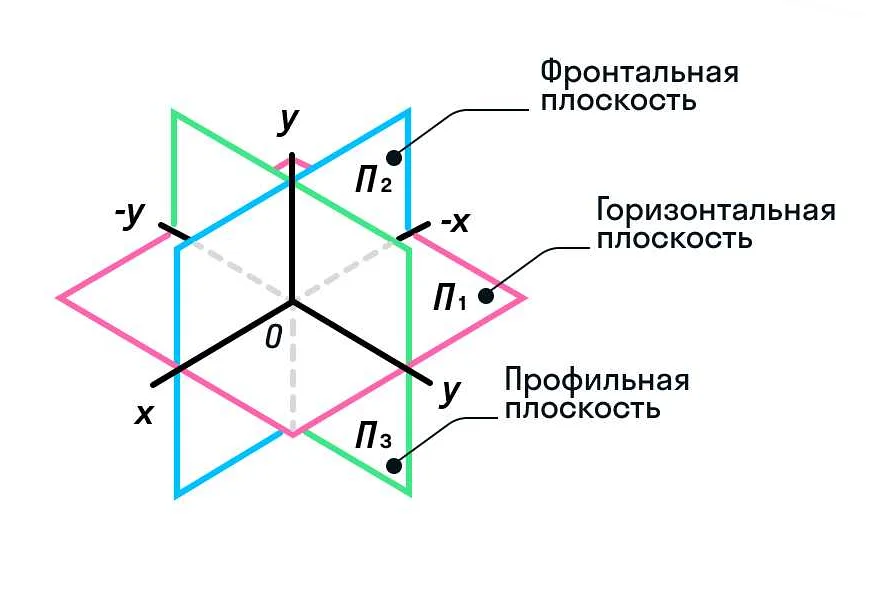
Геометрическое представление плоскости часто используется для решения задач и построения графиков. Плоскость можно представить с помощью координатной системы, где каждая точка на плоскости имеет уникальные координаты, состоящие из двух чисел — x и y.

Координатная плоскость делится на четыре квадранта, которые образуются пересечением осей координат. Квадранты помогают определить положение точек относительно начала координат.

• В первом квадранте x и y положительны, и точки находятся в верхней правой части плоскости.
• Во втором квадранте x отрицательно, а y положительно, и точки находятся в верхней левой части плоскости.
• В третьем квадранте и x, и y отрицательны, и точки находятся в нижней левой части плоскости.
• В четвертом квадранте x положительно, а y отрицательно, и точки находятся в нижней правой части плоскости.

Геометрическое представление плоскости позволяет решать различные задачи, связанные с изучением двумерных объектов и их взаимодействием. Оно также является основой для изучения более сложных понятий и концепций, таких как трехмерное пространство и многомерные геометрические объекты.

Основные свойства плоскости

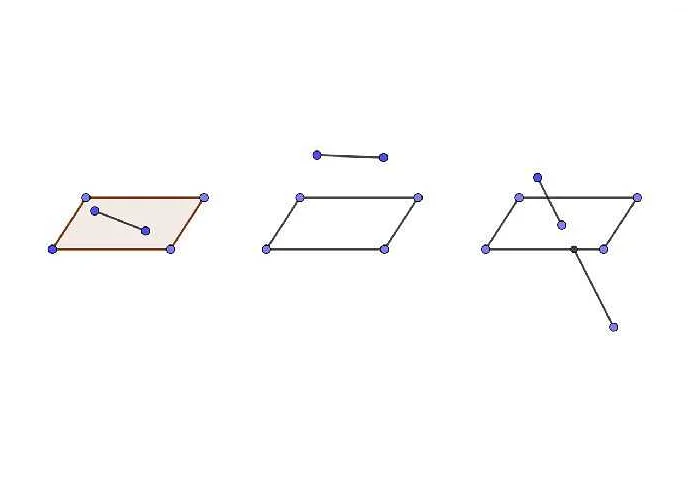
Основные свойства плоскости включают:

1. Прямые на плоскости: На плоскости можно провести множество прямых линий, и они не пересекаются друг с другом.

2. Углы на плоскости: Две прямые линии, пересекающиеся на плоскости, образуют угол. Угол может быть острый, прямой или тупой, в зависимости от его величины.

3. Расстояние между точками: На плоскости можно определить расстояние между двумя точками с помощью формулы расстояния между двумя точками в прямоугольной системе координат.

4. Параллельность: Две прямые на плоскости называются параллельными, если они никогда не пересекаются, даже при продлении до бесконечности.

Эти свойства плоскости являются основными и наиболее важными для изучения геометрии и анализа в двумерном пространстве.

Уравнение плоскости

Уравнение плоскости имеет вид:

Ax + By + Cz + D = 0

Здесь A, B и C — коэффициенты, которые определяют вектор нормали к плоскости, а D — свободный член.

Уравнение плоскости можно также записать в векторной форме:

N·r + D = 0

Здесь N — вектор нормали к плоскости, r — радиус-вектор точки на плоскости.

Используя уравнение плоскости, мы можем определить, принадлежит ли точка плоскости или нет, а также находить пересечения плоскостей и другие геометрические свойства.

Уравнение плоскости — это важный инструмент в геометрии и применяется в различных областях математики, физики, инженерии и компьютерной графике.

Прямая и плоскость: взаимное расположение

Прямая и плоскость могут взаимодействовать и располагаться относительно друг друга по разным сценариям:

1. Прямая пересекает плоскость.

Если прямая пересекает плоскость, то она проходит через нее и имеет с ней одну или несколько общих точек. При этом прямая может пересекать плоскость под углом или быть параллельной ей.

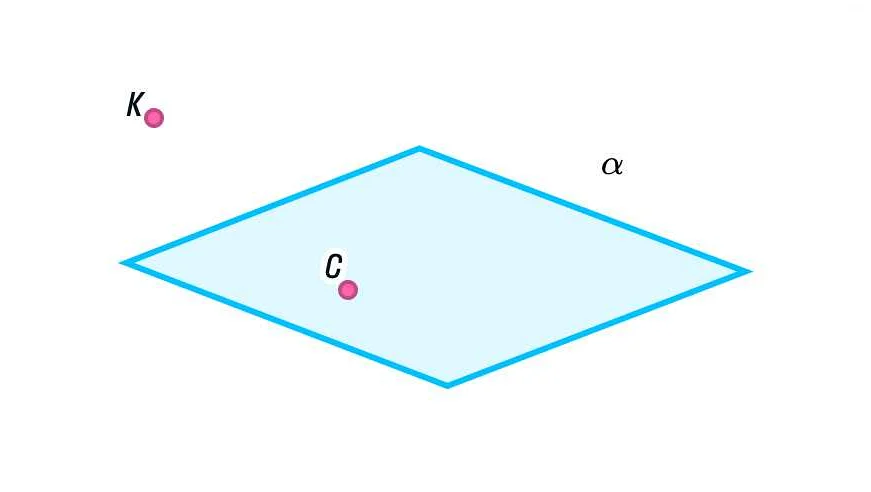
2. Прямая лежит в плоскости.

Если прямая лежит в плоскости, то она полностью находится внутри данной плоскости и не выходит за ее границы. Такая прямая может быть горизонтальной, вертикальной или наклонной относительно плоскости.

3. Прямая параллельна плоскости.

Если прямая параллельна плоскости, то она не пересекает и не лежит внутри плоскости. Такие прямые могут быть расположены в одной плоскости, но не имеют общих точек. Они остаются постоянно одинаково удаленными друг от друга.

Понимание взаимного расположения прямой и плоскости важно для решения задач и построения геометрических моделей. Эти основные понятия позволяют нам анализировать и понимать пространственные отношения в геометрии.

Пересечение плоскостей

Когда две плоскости пересекаются, они образуют прямую линию, которая называется линией пересечения. Линия пересечения находится в каждой из плоскостей и является их общим элементом.

Пересечение плоскостей может иметь различные формы, в зависимости от угла между плоскостями и их направления. Если плоскости пересекаются под прямым углом, линия пересечения будет вертикальной и образует прямой угол с плоскостями. Если угол между плоскостями не прямой, линия пересечения будет наклонной и образует острый или тупой угол с плоскостями.

Пересечение плоскостей широко используется в геометрии и аналитической геометрии для решения различных задач. Например, при решении систем уравнений с двумя неизвестными можно использовать пересечение двух плоскостей для нахождения точки их пересечения, которая будет являться решением системы.

Все это позволяет нам лучше понять структуру и свойства плоскостей в пространстве и применять их в решении различных задач.

Примеры практического использования плоскости

1. Архитектура и строительство: Плоскость используется в проектировании зданий и сооружений. Архитекторы и инженеры используют плоскость для создания планов зданий, которые показывают расположение стен, окон, дверей и других элементов.
2. Графика и дизайн: В графическом дизайне плоскость используется для создания различных иллюстраций, логотипов, афиш и других визуальных материалов. Дизайнеры используют плоскость для размещения элементов изображения и создания гармоничного композиционного решения.
3. География: Плоскость используется для изображения карт и планов различных местностей. Географы и навигаторы используют плоскость для описания местности, определения координат точек и построения маршрутов.
4. Инженерия: В инженерии плоскость используется для создания чертежей и схем различных механизмов и систем. Инженеры используют плоскость для определения размеров, формы и расположения деталей, а также для моделирования и анализа сложных конструкций.
5. Математика и физика: Плоскость — основа для изучения геометрии, алгебры, тригонометрии и других математических дисциплин. Математики и физики используют плоскость для решения различных задач, проведения экспериментов и построения графиков.

Это лишь некоторые примеры использования плоскости в нашей повседневной жизни. Очевидно, что понимание и умение работать с плоскостью являются важными навыками, которые могут быть полезны в различных областях деятельности.

Вопрос-ответ:

Что такое плоскость?

Плоскость — это геометрическая фигура, которая не имеет толщины и состоит из бесконечного количества точек, расположенных на одной и той же плоскости.

Как можно представить плоскость?

Представить плоскость можно как двумерную поверхность, которая простирается бесконечно во всех направлениях.

Какие свойства имеет плоскость?

Плоскость имеет несколько свойств. Во-первых, через любые две точки плоскости можно провести прямую линию, которая будет лежать на этой плоскости. Во-вторых, все углы на плоскости равны. Наконец, на плоскости можно провести прямую параллельно любой другой прямой.

Какие примеры плоскостей можно привести?

Примерами плоскостей могут быть поверхность стола, лист бумаги, пол нашей комнаты или даже поверхность земли на небольшом участке.

Какое значение имеет плоскость в математике?

Плоскость имеет огромное значение в математике, так как она является основой для изучения геометрии и алгебры. Множество геометрических фигур, таких как треугольник или круг, определяется на плоскости.

Что такое плоскость в математике?

Плоскость в математике — это двумерная геометрическая фигура, которая не имеет объема и может быть представлена как бесконечно тонкий лист. Она состоит из бесконечного числа точек и не имеет начала или конца.

Как можно представить плоскость?

Плоскость можно представить как ровную поверхность без толщины. Визуально она может быть изображена на бумаге или на экране компьютера с помощью геометрических фигур и линий. Например, можно представить плоскость в виде прямоугольника или треугольника.