Что такое по в математике
Содержимое
- 1 Что такое по в математике
- 1.1 Понятие «по» в математике: что это такое?
- 1.2 Определение «по» в математике: основные характеристики
- 1.3 Примеры использования «по» в математике
- 1.4 По в арифметике: основные свойства
- 1.5 По в геометрии: интересные факты
- 1.6 По в алгебре: примеры задач
- 1.7 По в тригонометрии: практическое применение
- 1.8 По в статистике: анализ данных
- 1.9 Вопрос-ответ:
- 1.10 Видео по теме:
По в математике – это понятие, которое обозначает принадлежность некоторого объекта или явления определенному классу или множеству. По в математике используется для описания отношений и свойств между элементами и множествами, а также для формулирования аксиом и теорем. Узнайте больше о том, что такое по в математике и как оно применяется в различных областях науки.
Понятие «по» является одним из фундаментальных понятий в математике. В математике «по» используется для обозначения отношения или операции между двумя или более объектами. Оно имеет широкий спектр применений и встречается в различных математических дисциплинах, таких как алгебра, геометрия, теория чисел и других.
Существует несколько основных видов «по» в математике. Одним из самых распространенных видов является «по» в алгебре. В алгебре «по» обозначает соотношение или равенство между двумя выражениями. Например, «5 + 3 по 8» означает, что сумма 5 и 3 равна 8. Это позволяет нам решать уравнения и выполнять различные операции с числами.
Понятие «по» также применяется в геометрии. В геометрии «по» может обозначать направление или отношение между геометрическими фигурами. Например, «точка А по прямой AB» означает, что точка А лежит на прямой AB. Это позволяет нам определять и изучать различные геометрические свойства и отношения.
Все эти примеры и множество других демонстрируют важность и широкое применение «по» в математике. Оно является основой для понимания и решения различных математических проблем и задач. Без понимания «по» невозможно полноценно изучать и применять математику в различных областях науки и техники.
Понятие «по» в математике: что это такое?
В математике понятие «по» часто используется для обозначения действий или операций, которые выполняются над элементами множества. Это позволяет применять одно и то же действие к различным объектам и получать результаты в соответствии с определенными правилами.
Например, если рассматривать операцию умножения в натуральных числах, то выражение «3 по 4» означает, что нужно взять число 3 и сложить его с самим собой 4 раза: 3 + 3 + 3 + 3 = 12. Таким образом, «по» в данном случае указывает на повторение операции сложения несколько раз.
Понятие «по» также может использоваться для обозначения действий над матрицами. Например, если у нас есть матрица A и требуется умножить ее на матрицу B, то запись «A по B» означает, что каждый элемент матрицы A нужно умножить на соответствующий элемент матрицы B и сложить полученные произведения. Таким образом, «по» в данном случае указывает на покоординатное умножение элементов матриц.
Операция «по»Пример
| Сложение | 2 по 3 = 2 + 2 + 2 = 6 |
| Умножение | 3 по 4 = 3 + 3 + 3 + 3 = 12 |
| Покоординатное умножение | Матрица A по B = (A11 * B11) + (A12 * B12) + (A21 * B21) + (A22 * B22) |
Таким образом, понятие «по» в математике позволяет обозначать действия, выполняемые над элементами множества, и является важным инструментом для решения различных задач и применения математических операций.
Определение «по» в математике: основные характеристики

По может быть использовано в различных контекстах и иметь различные значения. Например, в алгебре по может обозначать операцию, выполняемую с каждым элементом множества. В геометрии по может указывать направление движения или отношение между двумя объектами.
Примеры использования по в математике:
- Умножение числа по 2: каждый элемент числового множества умножается на 2.
- Деление числа по 3: каждый элемент числового множества делится на 3.
- Движение по прямой: движение вдоль прямой линии.
- Условие по возрастанию: упорядочивание элементов в порядке возрастания.
Важно отметить, что значение по зависит от контекста и может иметь различные интерпретации в разных областях математики. Поэтому при использовании этого термина необходимо учитывать контекст и ясно определить его значение.
Примеры использования «по» в математике
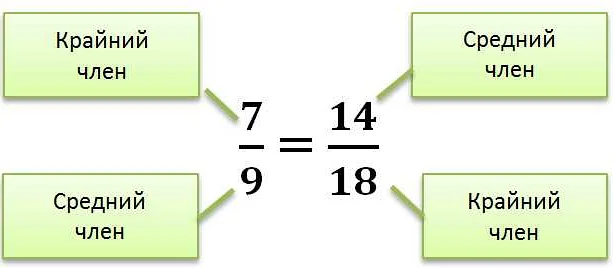
В математике термин «по» используется для указания действия, которое выполняется с каждым элементом некоторого множества или с каждым членом некоторой последовательности. Вот несколько примеров использования «по» в математике:
- Поэлементное сложение двух векторов: ai + bi = ci, где i принимает значения от 1 до n. Это означает, что каждый элемент вектора a складывается с соответствующим элементом вектора b, и результат записывается в вектор c.
- Поэлементное умножение двух матриц: aij * bij = cij, где i принимает значения от 1 до m, а j — от 1 до n. Здесь каждый элемент матрицы a умножается на соответствующий элемент матрицы b, и результат записывается в матрицу c.
- Сумма ряда: S = a1 + a2 + … + an. Здесь «по» указывает на то, что каждый член ряда ai при i от 1 до n суммируется.
- Поэлементное деление одного вектора на другой: ai / bi = ci, где i принимает значения от 1 до n. В этом случае каждый элемент вектора a делится на соответствующий элемент вектора b, и результат записывается в вектор c.
- Поэлементное возведение в степень: ai^bi = ci, где i принимает значения от 1 до n. Здесь каждый элемент a возводится в степень, указанную соответствующим элементом вектора b, и результат записывается в вектор c.
Такие примеры использования «по» в математике помогают выполнить операции с каждым элементом некоторого множества или последовательности, делая вычисления более компактными и понятными.
По в арифметике: основные свойства
Основные свойства по включают:
- По симметрично: если a по b, то и b по a.
- По неассоциативно: не выполняется свойство (a по b) по c = a по (b по c).
- По дистрибутивно относительно сложения: (a + b) по c = (a по c) + (b по c).
- По дистрибутивно относительно умножения: (a * b) по c = (a по c) * (b по c).
- По дистрибутивно относительно вычитания: (a — b) по c = (a по c) — (b по c).
Примеры:
- По 12 по 5 равно 2, так как 12 можно разделить на 5, получив 2 и остаток 2.
- По 7 по 3 равно 2, так как 7 можно разделить на 3, получив 2 и остаток 1.
- По 15 по 4 равно 3, так как 15 можно разделить на 4, получив 3 и остаток 3.
По в геометрии: интересные факты

Интересный факт о по: перпендикулярные прямые всегда пересекаются под прямым углом (90 градусов). То есть, если две прямые перпендикулярны друг другу, то они пересекаются так, что образуют прямой угол.
Еще один интересный факт: параллельные прямые никогда не пересекаются, они всегда остаются на одинаковом расстоянии друг от друга. Такие прямые никогда не сходятся и не расходятся.
Существует также понятие скользящего по. Это означает, что две плоскости скользят друг по другу, параллельно двигаясь вдоль друг друга. Такое движение создает по между плоскостями.
По в геометрии – это важное понятие, которое помогает описывать отношения и свойства прямых и плоскостей. Разные типы по имеют свои особенности и применяются в различных ситуациях.
По в алгебре: примеры задач

Пример 1:
Дано множество A = {1, 2, 3, 4, 5, 6}. Найти все элементы множества A, которые делятся на 2.
Решение: Чтобы найти все элементы множества A, которые делятся на 2, необходимо перебрать каждый элемент множества и проверить его на делимость на 2. В данном случае, элементы 2, 4 и 6 делятся на 2, поэтому ответом будет множество B = {2, 4, 6}.
Пример 2:
Даны два множества A = {1, 2, 3} и B = {2, 3, 4}. Найти все элементы, которые принадлежат обоим множествам.
Решение: Чтобы найти все элементы, которые принадлежат обоим множествам A и B, необходимо перебрать каждый элемент первого множества и проверить его на принадлежность к второму множеству. В данном случае, элементы 2 и 3 принадлежат обоим множествам, поэтому ответом будет множество C = {2, 3}.
Пример 3:
Даны множества A = {1, 2, 3} и B = {4, 5, 6}. Найти все элементы, которые принадлежат только одному из множеств.
Решение: Чтобы найти все элементы, которые принадлежат только одному из множеств A или B, необходимо объединить оба множества и исключить из объединения элементы, которые принадлежат обоим множествам. В данном случае, объединение множеств A и B равно {1, 2, 3, 4, 5, 6}, а пересечение равно {}. Таким образом, ответом будет множество D = {1, 2, 3, 4, 5, 6} \ {} = {1, 2, 3, 4, 5, 6}.
Таким образом, по в алгебре является важным понятием, которое позволяет описывать взаимосвязь между элементами множества. Примеры задач помогут лучше разобраться с этим понятием и применять его в практических задачах.
По в тригонометрии: практическое применение
Параметр по широко используется в тригонометрии для вычисления значений тригонометрических функций — синуса, косинуса, тангенса и т.д. Он позволяет определить отношение между сторонами прямоугольного треугольника и его углами.
Использование параметра по в тригонометрии находит свое применение в различных областях, таких как физика, инженерия, компьютерная графика и других. Например, в физике он помогает определить положение и движение объектов, в инженерии — расчеты сил и углов наклона, а в компьютерной графике — создание 3D-моделей и анимации.
Параметр по в также используется для решения различных задач, связанных с геометрией, тригонометрией и аналитической геометрией. Например, он позволяет определить углы между прямыми и плоскостями, находить расстояния между точками и многое другое.
Тригонометрическая функцияФормулаОписание
| Синус | sin(θ) = противолежащая сторона / гипотенуза | Отношение противолежащей стороны к гипотенузе прямоугольного треугольника |
| Косинус | cos(θ) = прилежащая сторона / гипотенуза | Отношение прилежащей стороны к гипотенузе прямоугольного треугольника |
| Тангенс | tan(θ) = противолежащая сторона / прилежащая сторона | Отношение противолежащей стороны к прилежащей стороне прямоугольного треугольника |
По в статистике: анализ данных
По в может быть выражено в виде процента или десятичной дроби. Он часто используется для измерения вероятности события или частоты его появления в выборке или популяции.
Например, предположим, что в опросе было задано вопрос: «Какую оценку вы бы дали этому продукту?». Ответы могут быть «удовлетворительно», «хорошо» или «отлично». Если 50% респондентов выбрали ответ «отлично», то по в этого ответа составляет 0,5 или 50%.
По в также может быть использован для сравнения данных в разных группах или сравнения данных до и после введения некоторых изменений или вмешательств.
Анализ данных с использованием по в может помочь в выявлении тенденций, принятии решений и прогнозировании результатов в различных областях, таких как маркетинг, экономика, социология и медицина.
Примеры использования по в в статистике:
- Исследование популярности брендов: по в может показать, какую долю рынка занимает каждый бренд в определенной отрасли.
- Оценка результатов эксперимента: по в может показать, какое количество испытуемых достигло желаемого результата после применения нового лекарства или метода лечения.
- Анализ предпочтений потребителей: по в может показать, какой процент потребителей предпочитает определенный продукт или услугу.
Знание по в статистике позволяет проводить более точные и информативные анализы данных, что помогает в принятии обоснованных решений и планировании дальнейших действий.
Вопрос-ответ:
Что такое по в математике?
По в математике – это математическое отношение, которое связывает две величины, такие, что при изменении одной величины, другая также изменяется. Оно обозначается символом «по» и означает, что одна величина зависит от другой.
Какие примеры можно привести по в математике?
Примеры по в математике можно найти в разных областях. Например, в физике по встречается при описании зависимости между скоростью и временем, или между силой и перемещением. В экономике по в может подразумевать зависимость между спросом и ценой товара. В математических уравнениях по в также широко используется, например, в уравнении прямой y = kx + b, где k и b — коэффициенты, определяющие зависимость между x и y.
Как определить по в математике?
По в математике можно определить, если есть две величины, и при изменении одной из них, другая тоже меняется. Это отношение можно представить в виде уравнения или графика, которые показывают зависимость между величинами. Если изменение одной величины приводит к изменению другой, то можно сказать, что между ними существует по в.
Какие свойства имеет по в математике?
По в математике обладает несколькими свойствами. Во-первых, если одна величина зависит от другой, то при увеличении (или уменьшении) одной величины, другая также увеличивается (или уменьшается). Во-вторых, существует понятие прямой и обратной зависимости: если изменение одной величины приводит к прямому изменению другой (т.е. они движутся в одном направлении), то это прямая зависимость, если они движутся в противоположных направлениях, то это обратная зависимость.
Как построить график по в математике?
Для построения графика по в математике необходимо иметь данные о значениях двух величин, между которыми существует по в. На оси абсцисс откладываются значения одной величины, на оси ординат — значения другой величины. Затем, в зависимости от вида по в (прямой или обратной зависимости), точки соединяют прямой или кривой линией. График показывает, как изменение одной величины влияет на другую.
Что такое по в математике?
По (или повторение) в математике — это операция, при которой определенное значение повторяется несколько раз. Например, если мы говорим о по 3, то это означает, что определенное значение будет повторяться три раза.



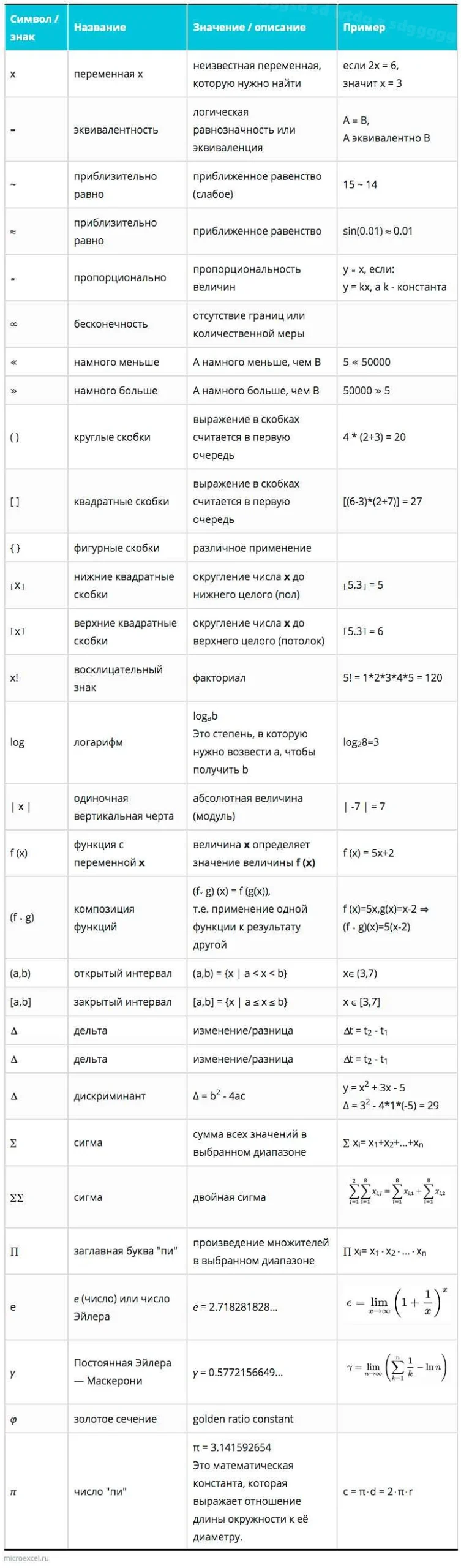
В математике понятие «по» является одним из основных и широко используется в различных областях этой науки. «По» — это префикс, который обозначает распределение или отношение элементов множества. Он позволяет проводить классификацию или группировку объектов по определенному признаку. Например, если мы говорим о числах от 1 до 10, то можем разделить их на четные и нечетные по числу деления на 2. Также «по» применяется в алгебре, геометрии, теории вероятностей и других разделах математики. Он помогает упорядочить информацию и облегчить ее анализ. Все это делает понятие «по» неотъемлемой частью математического аппарата и помогает нам лучше понять мир цифр и формул.
Статья очень понравилась! Я всегда интересовалась математикой, но понятие «по» мне оставалось не совсем ясным. Благодаря данной статье, я легко и просто разобралась в этом вопросе. По-моему, понятие «по» связано с отношением между двумя величинами. Например, когда говорят «десять к по два», это значит, что одно число делится на другое без остатка. Также, в статье были приведены примеры, которые очень хорошо помогли мне понять, как использовать понятие «по» в математике. В целом, статья очень познавательная и полезная для всех, кто хочет разобраться в этом вопросе. Спасибо за интересную и понятную статью!
Я всегда интересуюсь математикой, поэтому статья на тему «Что такое по в математике: определение и примеры» звучит очень заманчиво. Однако, мне было бы полезно узнать больше о термине «по» и о том, как его можно применить в математике. Может быть, это некий оператор или функция? Я также заинтересован в примерах использования этого термина, чтобы лучше понять его значение и важность. Буду ждать с нетерпением, чтобы прочитать эту статью и расширить свои знания в области математики.