Что такое полигон в математике

Полигон в математике — геометрическая фигура, образованная соединением отрезков между точками на плоскости. Полигон может быть выпуклым, невыпуклым или самопересекающимся, и его форма и размеры определяются координатами вершин. В данной статье рассматривается определение полигона, его свойства и основные типы полигонов в математике.

Полигон — это геометрическая фигура, состоящая из отрезков, соединяющих вершины. В математике полигоны изучаются в разделе геометрии. Они имеют несколько особенностей, которые делают их интересными для исследования.

Во-первых, полигон может быть выпуклым или невыпуклым. Выпуклый полигон — это такая фигура, у которой все внутренние углы меньше 180 градусов. Невыпуклый полигон имеет внутренние углы, большие 180 градусов. Это является одной из особенностей полигонов, и изучение их свойств помогает понять, какие углы возможны в геометрии.

Во-вторых, полигон может быть ограничен и неограничен. Ограниченный полигон имеет конечное количество вершин и ограничен площадью. Неограниченный полигон не имеет начала и конца и может быть бесконечно продолжаемым в любом направлении. Эта особенность полигонов позволяет изучать их различные формы и размеры.

Примером полигона может служить треугольник. Он является простейшим полигоном и имеет три вершины и три отрезка, соединяющих их. Треугольник может быть как выпуклым, так и невыпуклым, в зависимости от величины его внутренних углов.

Полигоны играют важную роль в геометрии и имеют множество применений в различных областях, таких как архитектура, графика, компьютерная моделирование и техническое черчение. Изучение полигонов позволяет лучше понять пространственные отношения и свойства геометрических фигур, что помогает в решении различных задач и проблем.

Полигон в математике: определение, особенности, примеры

Особенностью полигона является то, что все его внутренние углы являются меньшими двух прямых углов (180 градусов). Также, сумма всех внутренних углов полигона всегда равна (n-2) * 180 градусов, где n — количество вершин полигона.

Для примера, рассмотрим многоугольник с тремя вершинами — треугольник. Треугольник является простейшим примером полигона. У него три вершины и три стороны. Сумма внутренних углов треугольника всегда равна 180 градусов. Треугольник может быть равносторонним, равнобедренным или произвольным.

Другим примером полигона является четырехугольник, или квадрат. Квадрат имеет четыре равные стороны и четыре прямых угла. Сумма внутренних углов квадрата также равна 360 градусов.

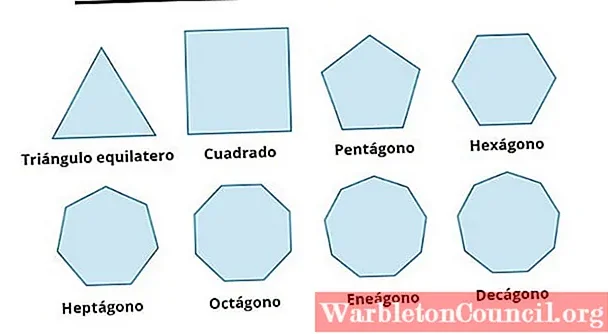
Более сложные примеры полигонов включают пятиугольник, шестиугольник, семиугольник и так далее. Каждый полигон имеет свои особенности и свойства, которые могут быть изучены с помощью геометрических методов.

Видео по теме:

Понятие полигона в математике

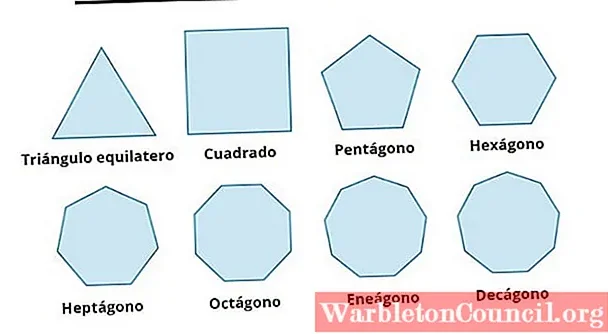
Основной особенностью полигона является то, что он имеет замкнутую фигуру, то есть последняя сторона соединяется с первой. Полигон может быть как плоским, так и пространственным, в зависимости от количества его сторон.

Полигоны широко используются в геометрии для изучения и описания различных фигур и объектов. Они могут быть прямоугольными, треугольными, многоугольными и т. д. Каждый полигон имеет свои уникальные свойства и характеристики, которые определяются его формой и размерами.

Пример полигона — треугольник, который является наиболее простым полигоном. У треугольника три стороны и три вершины. Он также обладает свойствами, такими как сумма углов треугольника равна 180 градусам и неравенство треугольника, которое гласит: сумма длин двух сторон треугольника всегда больше длины третьей стороны.

Основные характеристики полигона

1. Количество сторон: полигон может иметь любое количество сторон, начиная от трех и больше. Полигоны с тремя, четырьмя и пяти сторонами называются, соответственно, треугольником, четырехугольником и пятиугольником.

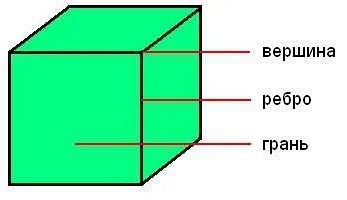
2. Вершины: вершины полигона — это точки пересечения сторон. Чем больше сторон у полигона, тем больше вершин у него будет.

3. Углы: у полигона есть внутренние углы, образованные сторонами, и внешние углы, образованные продолжением сторон за вершинами. Сумма внутренних углов полигона всегда равна 180 градусов, независимо от количества сторон.

4. Периметр: периметр полигона — это сумма длин всех его сторон. Он позволяет измерить длину границы фигуры.

5. Площадь: площадь полигона — это показатель его площади, выраженный в квадратных единицах. Площадь полигона можно вычислить с помощью различных методов, в зависимости от его формы и размеров.

Это лишь некоторые из основных характеристик полигона. Каждая из них играет важную роль в определении и анализе геометрических фигур.

Вопрос-ответ:

Что такое полигон в математике?

Полигон в математике — это плоская фигура, образованная отрезками, называемыми сторонами, которые соединяют вершины. У полигона может быть любое количество сторон, начиная от трех.

Какие особенности у полигона в математике?

У полигона есть несколько особенностей. Во-первых, все его стороны и углы равны между собой. Во-вторых, сумма всех углов полигона всегда будет равна 180 градусам. Кроме того, у полигона может быть выпуклая или невыпуклая форма.

Какие примеры полигонов можно привести?

Примерами полигонов могут быть треугольник, четырехугольник, пятиугольник, шестиугольник и так далее. Например, треугольник — это полигон с тремя сторонами, четырехугольник — с четырьмя сторонами, и так далее.

Как можно классифицировать полигоны по количеству сторон?

Полигоны можно классифицировать по количеству сторон следующим образом: треугольники (3 стороны), четырехугольники (4 стороны), пятиугольники (5 сторон) и так далее. Также существуют названия для полигонов с определенным количеством сторон, например, шестиугольник (6 сторон), семиугольник (7 сторон) и т.д.

Какое значение имеет сумма углов полигона?

Сумма углов полигона всегда будет равна 180 градусам. Например, для треугольника сумма его трех углов всегда будет равна 180 градусам, для четырехугольника — 360 градусам, для пятиугольника — 540 градусам и так далее. Это одна из особенностей полигонов в математике.

Что такое полигон в математике?

Полигон в математике — это замкнутая фигура, состоящая из отрезков, которые соединяют вершины. Он имеет конечное количество сторон и углов.

Какие особенности есть у полигона?

У полигона есть несколько особенностей. Во-первых, он является замкнутой фигурой, то есть первая и последняя вершины соединены отрезком. Во-вторых, сумма всех внутренних углов полигона равна (n-2)180 градусов, где n — количество сторон полигона. Также, каждая сторона полигона соединяет две вершины и имеет свою длину.

Типы полигонов

В математике существует различные типы полигонов, которые отличаются своей формой и свойствами:

1. Треугольник — полигон с тремя сторонами и тремя углами.

2. Четырехугольник — полигон с четырьмя сторонами и четырьмя углами.

3. Пятиугольник — полигон с пятью сторонами и пятью углами.

4. Шестиугольник — полигон с шестью сторонами и шестью углами.

5. Многоугольник — полигон с большим количеством сторон и углов. Многоугольником можно назвать полигон с любым числом сторон от трех и более.

Каждый тип полигона имеет свои особенности и свойства, которые могут быть использованы при решении различных задач и проблем в математике и других науках.

Свойства полигонов

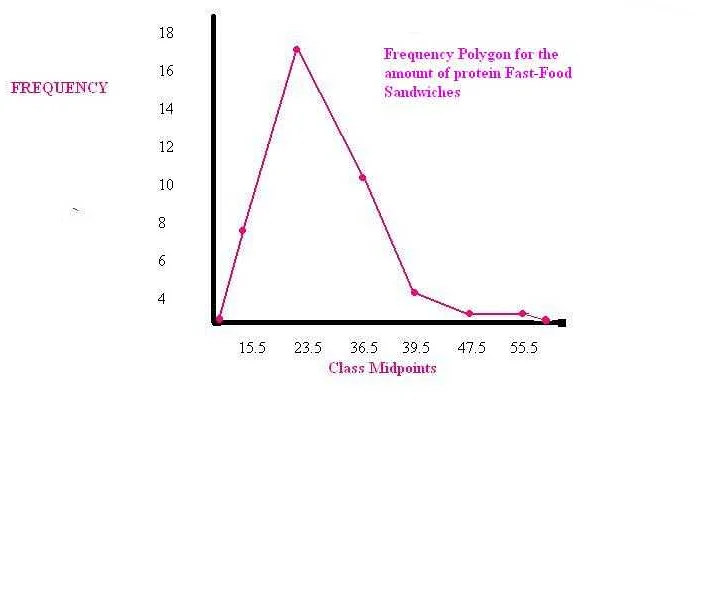
Вот некоторые основные свойства полигонов:

1. Сумма внутренних углов полигона всегда равна 180 градусам. Это свойство называется суммой углов полигона.
2. Сумма внешних углов полигона всегда равна 360 градусам. Это свойство называется суммой внешних углов полигона.
3. Длины сторон полигона могут быть разными, но они должны быть положительными числами.
4. Если все стороны полигона равны, то полигон называется правильным.
5. Все внутренние углы правильного полигона равны между собой.

Например, треугольник — это полигон с тремя сторонами и тремя внутренними углами. Если все три угла треугольника равны между собой, то треугольник является равносторонним. Если две стороны треугольника равны между собой, то треугольник является равнобедренным.

Полигоны широко используются в геометрии и имеют множество применений в различных областях науки и техники.

Примеры полигонов в математике

• Треугольник — это полигон, состоящий из трех сторон. У треугольника три вершины и три угла.
• Квадрат — это полигон, состоящий из четырех равных сторон. У квадрата четыре угла, каждый из которых равен 90 градусов.
• Пятиугольник — это полигон, состоящий из пяти сторон. У пятиугольника пять вершин и пять углов.
• Шестиугольник — это полигон, состоящий из шести сторон. У шестиугольника шесть вершин и шесть углов.

Это только несколько примеров полигонов, их может быть бесконечное множество. В математике полигоны являются важными объектами для изучения и решения различных задач.

Полигон в геометрии

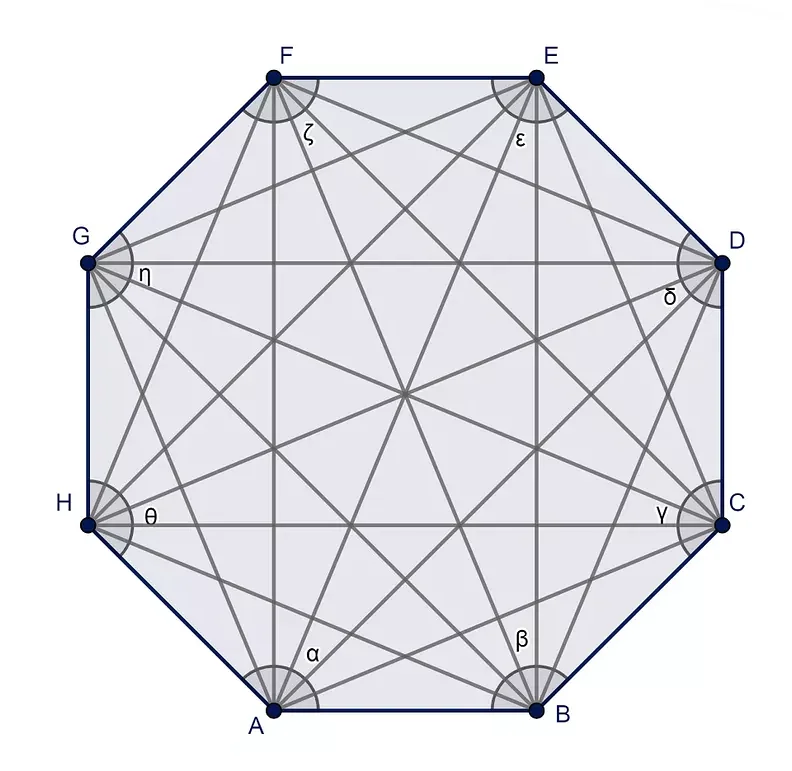
У полигона может быть любое количество вершин, но не менее трех. Полигоны могут быть разнообразных форм, таких как треугольники, четырехугольники, пятиугольники и так далее.

Чтобы полигон назывался выпуклым, все его внутренние углы должны быть меньше 180 градусов. Невыпуклый полигон имеет хотя бы один внутренний угол, равный или больший 180 градусов.

Особенностью полигонов является то, что сумма всех их внутренних углов всегда равна (n-2)*180 градусов, где n — количество вершин полигона.

Примерами полигонов могут служить треугольник (3 вершины), четырехугольник (4 вершины), пятиугольник (5 вершин) и так далее. Каждый полигон имеет свои характеристики, такие как длины сторон, величины углов и периметр.

Полигон в топологии

В топологии полигон представляет собой фигуру, которая состоит из конечного числа прямых отрезков, называемых сторонами, и их вершин. При этом стороны могут соприкасаться только в вершинах и не пересекаться.

Особенностью полигона в топологии является то, что он может быть замкнутым или незамкнутым. Замкнутый полигон представляет собой фигуру, у которой первая и последняя вершины совпадают, а незамкнутый — фигуру, у которой первая и последняя вершины не совпадают.

Примером полигона в топологии может служить треугольник, состоящий из трех сторон и трех вершин. В этом случае треугольник будет замкнутым полигоном.

Полигон в топологии является важным понятием, используемым при изучении топологических пространств и их свойств. Он позволяет описать геометрические объекты и определить их особенности.