Что такое прямая математика

Прямая математика — это область математики, которая изучает прямые линии, их свойства и применение. В рамках этой науки исследуются уравнения прямых, их геометрические свойства, а также методы решения задач, связанных с прямыми линиями. Прямая математика широко применяется в геометрии, физике, инженерии и других областях науки и техники.

Прямая математика — одна из основных разделов математики, изучающая свойства и закономерности прямых линий. Прямая математика является основой для понимания и решения множества задач в различных областях науки и техники. Умение работать с прямыми линиями является важным навыком при решении геометрических задач, а также в аналитической геометрии и физике.

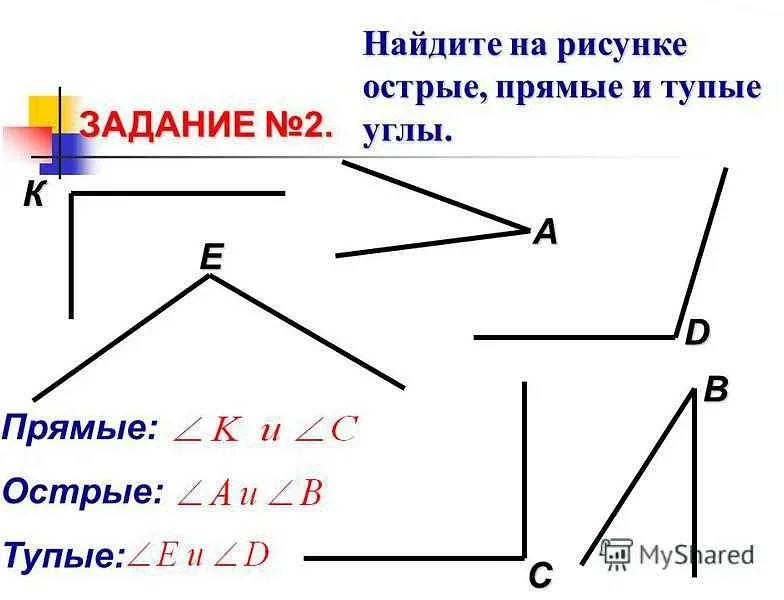
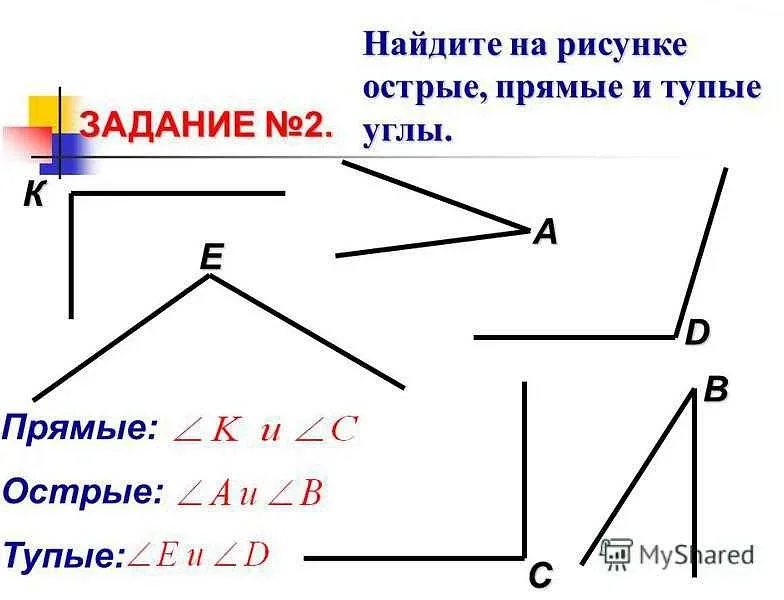
В прямой математике изучаются основные принципы построения прямых линий, их свойства и взаимное расположение. Важным понятием в прямой математике является угол, который определяет взаимное положение двух прямых линий. Угол может быть прямым, остроугольным или тупым. Он изучается с помощью специальных формул и методов, которые позволяют рассчитывать его величину и определять его тип.

Прямая математика также занимается изучением прямых линий в разных системах координат. Одна из основных систем координат, используемых в прямой математике, — декартова система координат. В декартовой системе координат прямая линия представлена уравнением вида y = kx + b, где k — наклон прямой, а b — ее смещение по вертикали.

Прямая математика является одной из фундаментальных дисциплин математики и широко применяется во множестве научных и практических задач. Она позволяет анализировать и моделировать различные явления, а также решать сложные задачи в различных областях, включая физику, инженерию и экономику.

Прямая математика: что это и основные принципы

Прямая математика имеет свои основные принципы, которые позволяют строить различные доказательства и решать задачи. Основными принципами прямой математики являются:

1. Аксиомы: базовые утверждения, которые принимаются без доказательства. Например, одна из аксиом прямой математики гласит, что через две различные точки проходит единственная прямая.
2. Теоремы: утверждения, которые могут быть доказаны на основе аксиом и других теорем. Например, теорема Пифагора в прямой математике устанавливает соотношение между длинами сторон прямоугольного треугольника.
3. Доказательства: логические рассуждения и последовательность шагов, которые позволяют установить истинность или ложность утверждения. Доказательства в прямой математике строятся на основе аксиом и ранее доказанных теорем.

Прямая математика является одной из основных дисциплин в математике и имеет широкое применение в различных областях, таких как физика, инженерия и компьютерная графика.

Важно понимать, что прямая математика – это лишь одна из множества ветвей математики и не охватывает всю ее область.

Определение прямой математики

Прямая математика основывается на строгих логических рассуждениях и использует формализованный язык символов и символических операций. Она занимается изучением математических объектов, таких как числа, функции, графы, векторы и многие другие, а также разработкой методов и алгоритмов для работы с ними.

Прямая математика позволяет решать разнообразные задачи, связанные с вычислениями, моделированием, анализом данных и принятием рациональных решений. Она играет важную роль в науке, технике, экономике, физике, информатике и многих других областях, где требуется точное и строгое мышление.

Основные принципы прямой математики включают аксиомы, определения, теоремы и доказательства. Аксиомы – это базовые утверждения, которые принимаются без доказательства. Определения – это точные и однозначные описания математических понятий. Теоремы – это утверждения, которые могут быть доказаны на основе аксиом и определений. Доказательства – это логические цепочки рассуждений, которые объясняют, почему та или иная теорема является истинной.

Прямая математика является неотъемлемой частью нашего понимания мира и играет ключевую роль в развитии науки и технологий.

История прямой математики

Прямая математика, также известная как аналитическая геометрия, развилась в XVII веке благодаря работам французского математика Рене Декарта. Он впервые представил идею о том, что геометрические фигуры могут быть описаны числами и алгебраическими уравнениями.

Декарт ввел систему координат, которая сейчас широко используется в прямой математике и других областях науки. Он представил прямую как геометрический объект, определенный двумя осями — осью x и осью y. Это позволило связать геометрию с алгеброй и решать геометрические задачи с помощью алгебраических методов.

С развитием прямой математики появились новые концепции и методы. В XIX веке немецкий математик Карл Фридрих Гаусс разработал метод наименьших квадратов, который позволяет решать системы линейных уравнений и находить наилучшие аппроксимации функций.

В XX веке прямая математика стала основой для развития других математических дисциплин, таких как математический анализ, теория вероятностей, математическая физика и многие другие. Сегодня прямая математика широко применяется в научных и инженерных расчетах, компьютерной графике, финансовой аналитике и других областях.

ГодыСобытия

XVII век	Развитие прямой математики Рене Декартом
XIX век	Разработка метода наименьших квадратов Карлом Фридрихом Гауссом
XX век	Применение прямой математики в различных областях науки и техники

Применение прямой математики в повседневной жизни

Архитектура и дизайн Прямая математика помогает архитекторам и дизайнерам создавать пропорциональные и эстетически приятные строения и предметы. Они используют прямую математику для расчета и построения прямых линий, а также для создания гармоничных пропорций и форм.	Инженерия и строительство В инженерных и строительных отраслях прямая математика широко используется для расчетов и построения планов зданий, дорог и других инфраструктурных объектов. Инженеры и строители опираются на принципы прямой математики, чтобы обеспечить точность и прочность конструкций.
Навигация и картография Прямая математика играет важную роль в навигации и картографии. Она помогает определять координаты точек и маршрутов, а также строить карты с учетом прямых линий и геометрических принципов.	Финансы и бизнес Прямая математика используется в финансовой и бизнес-аналитике для анализа и прогнозирования трендов, расчета доходности инвестиций, определения рентабельности и принятия решений на основе численных данных.

Это лишь несколько примеров применения прямой математики в повседневной жизни. Она находит свое применение во многих других областях, помогая решать различные задачи, оптимизировать процессы и делать наши жизни более удобными и эффективными.

Основные принципы прямой математики

Основные принципы прямой математики:

• Принцип равенства: В прямой математике используется понятие равенства, которое означает, что два выражения или объекта имеют одно и то же значение или свойства. Равенство обладает несколькими основными свойствами, такими как симметричность, рефлексивность и транзитивность.
• Принцип операций: Прямая математика основывается на операциях, таких как сложение, вычитание, умножение и деление. Операции над числами на прямой линии выполняются в соответствии с определенными правилами и свойствами, такими как коммутативность, ассоциативность и дистрибутивность.
• Принцип порядка: В прямой математике используется понятие порядка, которое определяет отношение между числами на прямой линии. Числа могут быть упорядочены по возрастанию или убыванию. Порядок чисел позволяет сравнивать и упорядочивать их с помощью операций сравнения, таких как больше, меньше, больше или равно, меньше или равно.
• Принцип эквивалентности: Прямая математика работает с понятием эквивалентности, которое означает, что два выражения или объекта имеют одно и то же значение или свойства в определенном контексте. Эквивалентные выражения или объекты могут быть заменены друг на друга без изменения результата или свойств.
• Принцип доказательств: Прямая математика основывается на принципе доказательств, который требует логического обоснования и доказательства утверждений и теорем. Доказательства в прямой математике строятся на основе логических шагов и принципов, таких как аксиомы, определения и ранее доказанные утверждения.

Основные принципы прямой математики являются фундаментальными для понимания и применения математических концепций и операций на прямой линии. Они позволяют решать различные математические задачи, проводить логические рассуждения и доказательства, а также строить и анализировать модели и графики.

Преимущества изучения прямой математики

Изучение прямой математики имеет множество преимуществ, которые могут быть полезными как в повседневной жизни, так и в профессиональной деятельности:

1. Развитие логического мышления. Изучение прямой математики требует аналитического и логического мышления, что способствует его развитию. Эти навыки могут быть применены не только в математических задачах, но и в решении различных проблем во всех областях жизни.
2. Улучшение навыков решения проблем. Изучение прямой математики помогает развить навыки решения проблем, анализировать информацию, находить паттерны и вырабатывать стратегии для достижения целей.
3. Подготовка к профессиональным специальностям. Прямая математика играет важную роль во множестве профессиональных областей, таких как физика, инженерия, экономика и компьютерные науки. Изучение прямой математики позволяет приобрести необходимые навыки и знания для успешной карьеры в этих областях.
4. Повышение уверенности в себе. Способность решать сложные математические задачи и понимать абстрактные концепции прямой математики помогает развить уверенность в своих способностях и повысить самооценку.
5. Развитие критического мышления. Изучение прямой математики требует анализа и оценки информации, что способствует развитию критического мышления. Это навык, который может быть применен в различных сферах жизни для принятия обоснованных решений.

Изучение прямой математики имеет множество преимуществ, которые помогут развить навыки, необходимые для успешной жизни и карьеры. Она является основой для понимания более сложных математических концепций и может быть полезной во многих сферах жизни.

Связь прямой математики с другими областями

1. Геометрия. Прямая математика тесно связана с геометрией, и в частности, с аналитической геометрией. Аналитическая геометрия изучает геометрические объекты, используя алгебраические методы. Прямая математика предоставляет набор инструментов и методов для анализа и решения геометрических задач.
2. Физика. Прямая математика играет важную роль в физике, так как многие физические явления и законы могут быть описаны математическими моделями, включающими прямые и их свойства. Например, закон Гука в механике связывает силу, деформацию и упругую константу через прямую зависимость.
3. Экономика. В экономике прямая математика используется для моделирования экономических процессов и анализа экономических данных. Например, линейные уравнения и системы линейных уравнений широко применяются для моделирования спроса и предложения, определения оптимальных стратегий и решения проблем оптимизации.
4. Инженерия. В инженерии прямая математика является неотъемлемой частью. Она используется при проектировании и анализе различных систем, включая электрические, механические и тепловые системы. Прямая математика позволяет моделировать и оптимизировать работу систем и решать инженерные задачи.
5. Компьютерные науки. В компьютерных науках прямая математика имеет широкое применение. Например, алгоритмы и структуры данных, используемые в программировании, основаны на математических концепциях, включая прямую математику. Множество алгоритмов и методов оптимизации также основаны на линейной алгебре и прямой математике в целом.

Таким образом, прямая математика имеет широкое применение и связь с множеством других областей, что делает её важной и неотъемлемой частью современного мира и науки.

Инструменты прямой математики

1. Уравнения прямых: Прямая может быть определена с помощью уравнения, которое связывает координаты ее точек. Существуют различные способы записи уравнений прямых, например, в виде y = kx + b или ax + by + c = 0. Уравнения прямых позволяют анализировать их свойства и решать задачи, связанные с прямыми.
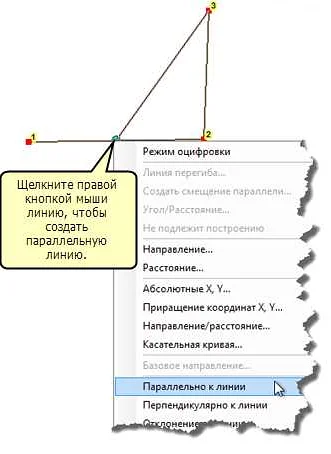
2. Геометрические построения: Для работы с прямыми и плоскостями в прямой математике широко используются геометрические построения. Например, построение перпендикуляра к заданной прямой, построение прямой, проходящей через заданную точку и параллельной другой прямой и т.д. Геометрические построения позволяют визуально представить прямые и решать задачи на их основе.
3. Аналитическая геометрия: Это раздел математики, в котором применяются алгебраические методы для изучения геометрических объектов, включая прямые и плоскости. Аналитическая геометрия позволяет описывать прямые и плоскости с помощью уравнений, а также проводить анализ их свойств и решать задачи на их основе.
4. Векторы: Векторы являются важным инструментом в прямой математике. Они позволяют описывать направление и длину прямой, а также проводить операции с ними, такие как сложение, вычитание и умножение на скаляр. Векторы также используются для решения задач на основе прямых и плоскостей.
5. Матрицы и линейная алгебра: Матрицы и линейная алгебра широко применяются в прямой математике для решения систем уравнений, связанных с прямыми и плоскостями. С помощью матриц и операций линейной алгебры можно анализировать и решать задачи, связанные с преобразованиями прямых и плоскостей.

Это лишь некоторые из инструментов, используемых в прямой математике. От выбора конкретного инструмента зависит эффективность решения задач и анализа прямых и плоскостей. Понимание и умение применять эти инструменты позволяет освоить прямую математику и использовать ее в различных областях знаний и практических задачах.

Полезные ресурсы для изучения прямой математики

Изучение прямой математики может быть интересным и познавательным процессом. Если вы хотите углубить свои знания в этой области или начать изучение с самого начала, вам могут пригодиться следующие ресурсы:

• Учебники по математике с разделами о прямой. Они предоставляют подробное объяснение основных понятий и принципов, а также содержат множество примеров и упражнений для тренировки.
• Онлайн-курсы и видеолекции. Существуют различные интерактивные курсы и видеоуроки, которые помогут вам разобраться в прямой математике. Вы сможете изучать материал в удобном для вас темпе и получать наглядное представление о различных концепциях.
• Математические форумы и сообщества. Присоединившись к соответствующим сообществам, вы сможете задавать вопросы, обсуждать сложности и находить решения вместе с другими людьми, которые также интересуются прямой математикой.
• Приложения и программы для мобильных устройств. Существуют различные приложения и программы, которые помогут вам практиковать прямую математику в любое время и в любом месте. Они часто включают в себя интерактивные задачи и игры, которые помогут вам запомнить и применить принципы.

Выберите подходящий для вас ресурс или комбинацию ресурсов, чтобы получить максимальную пользу от изучения прямой математики. Не забывайте, что практика и постоянное обновление знаний являются ключевыми элементами успеха в изучении любой математической темы.

Вопрос-ответ:

Что такое прямая математика?

Прямая математика — это раздел математики, который изучает принципы и методы решения задач, используя строгую логику и дедуктивные методы.

Какие основные принципы прямой математики?

Основные принципы прямой математики включают в себя строгость, точность, логическую последовательность и дедукцию. Прямая математика стремится к формализации и символическому представлению математических объектов и операций для достижения абсолютной ясности и корректности решений.

Какие преимущества прямой математики?

Прямая математика позволяет достичь высокой степени точности и надежности в решении математических задач. Она помогает развивать логическое мышление, аналитические навыки и способность к решению сложных проблем. Прямая математика также является основой для многих других наук и технических дисциплин, таких как физика, инженерия и компьютерные науки.

Какие примеры прямой математики можно найти в повседневной жизни?

Прямая математика применяется во многих сферах нашей жизни. Например, при планировании бюджета или расчете налогов, использовании статистики для анализа данных, проектировании зданий и мостов, разработке алгоритмов для компьютерных программ и многом другом. Она помогает нам оптимизировать ресурсы, принимать обоснованные решения и решать сложные задачи эффективно.

Видео по теме: