Что называют пропорцией математика 6 класс
Содержимое
- 1 Что называют пропорцией математика 6 класс
Пропорция в математике для 6 класса — это способ сравнения двух отношений или долей. Ученикам изучают основные понятия и правила работы с пропорциями, такие как понятие пропорциональности, правило трех пропорций и многие другие.
Пропорция — одна из основных тем математики, которую изучают в шестом классе. Пропорция является связью между четырьмя числами, при которой их отношения равны. В математике пропорция позволяет сравнивать и устанавливать равенства между различными величинами.
Пропорция состоит из двух частей — антецедента и консеквента. Антецедент — это пара чисел, стоящая перед двоеточием, а консеквент — пара чисел, стоящая после двоеточия. Пропорция записывается следующим образом: a:b = c:d. Здесь а и c — это антецедент, а b и d — консеквент. Пропорция считается верной, если отношение чисел в антецеденте равно отношению чисел в консеквенте.
Пример: рассмотрим пропорцию 1:2 = 3:6. В данном случае отношение чисел в антецеденте (1:2) равно отношению чисел в консеквенте (3:6), так как 1:2 = 3:6 = 1/2 = 3/6 = 0.5. Таким образом, пропорция является верной.
Пропорции встречаются в различных областях жизни. Например, в кулинарии пропорция используется при подсчете количества ингредиентов для приготовления блюд. В строительстве пропорция применяется при расчете соотношения размеров и доли материалов. В финансовой сфере пропорция используется при расчете процентных ставок и долей в инвестициях.
Изучение пропорций поможет шестиклассникам развить навыки анализа, логического мышления и решения математических задач. Понимание пропорций также поможет ученикам в будущем, когда они будут изучать более сложные математические темы, такие как алгебра и геометрия. Поэтому важно сделать основу пропорций максимально понятной и доступной для школьников.
Понятие пропорции
Пропорция записывается с использованием знака равенства и двоеточия. Например:
| а | : | b | = | c | : | d |
В данном примере а и b, а также c и d, образуют отношения, которые считаются равными. Пропорция может быть представлена как уравнение, где каждая сторона уравнения представляет отношение. Известные числа или величины называются известными пропорциональными частями, а неизвестные числа или величины — неизвестными пропорциональными частями.
Решение пропорции может быть выполнено с использованием кросс-мультипликации, то есть умножением чисел на противоположных сторонах пропорции и последующим сравнением полученных произведений. Если произведения равны, значит, пропорция выполняется.
Видео по теме:
Основные элементы пропорции

- Первый член — это число или выражение, расположенное перед знаком пропорции. Обозначается обычно как «а».
- Второй член — это число или выражение, расположенное после знака пропорции. Обозначается обычно как «b».
- Третий член — это число или выражение, расположенное перед знаком пропорции. Обозначается обычно как «с».
- Четвертый член — это число или выражение, расположенное после знака пропорции. Обозначается обычно как «d».
Пропорция записывается в виде а:б::с:д или а/б = с/д. Важно понимать, что пропорция указывает на равенство двух отношений между числами или выражениями. Если пропорция верна, то четыре члена пропорции связаны специальным отношением, называемым пропорциональностью.
Способы записи пропорции
Пропорции могут быть записаны в различных форматах, в зависимости от предпочтений и удобства использования. Вот некоторые из способов записи пропорции:
- С помощью двоеточия. Пропорция может быть записана в виде отношения двух чисел, разделенных двоеточием. Например: 2:3 = 4:6.
- С помощью дробей. Пропорция может быть записана в виде дроби, где числитель и знаменатель представляют соответствующие отношения. Например: 2/3 = 4/6.
- С помощью равенства. Пропорция может быть записана с помощью знака равенства, где отношение с одной стороны равно отношению с другой стороны. Например: 2/3 = 4/6.
- С помощью словесного описания. Пропорция может быть записана в виде словесного описания, указывающего отношение между различными элементами. Например: отношение числа студентов к числу учителей равно 2:1.
Выбор способа записи пропорции зависит от контекста и удобства использования. Важно быть внимательным при записи пропорции, чтобы избежать ошибок и правильно передать соотношение между элементами.
Примеры задач с пропорцией

1. В кафе за 4 часа 8 рабочих смогут приготовить 24 пирожных. Сколько пирожных сможет приготовить 12 рабочих за 6 часов?
Решение:
- Запишем пропорцию по условию задачи: 8 рабочих / 24 пирожных = 12 рабочих / х пирожных (где х — неизвестное число пирожных).
- Применим правило пропорции: 8 * х = 12 * 24.
- Решим уравнение: 8х = 12 * 24, х = (12 * 24) / 8.
- Вычислим значение х: х = 36.
Ответ: 12 рабочих смогут приготовить 36 пирожных за 6 часов.
2. Длина реки в 6 километрах соответствует масштабу 1:5000. Найдите масштаб, если известно, что длина реки составляет 10 километров.
Решение:
- Запишем пропорцию по условию задачи: 6 км / 1:5000 = 10 км / x.
- Применим правило пропорции: 6 * x = 10 * 5000.
- Решим уравнение: 6x = 10 * 5000, x = (10 * 5000) / 6.
- Вычислим значение x: x ≈ 8333,33.
Ответ: масштаб составляет примерно 1:8333,33.
Применение пропорции в повседневной жизни
Одним из примеров применения пропорции может быть ситуация, когда необходимо рассчитать количество ингредиентов для приготовления еды. Например, если в рецепте указано, что для приготовления пирога нужно взять 200 грамм муки и 4 яйца, можно использовать пропорцию для рассчета количества ингредиентов при изменении количества порций. Если нужно приготовить в два раза больше пирога, то вместо 200 грамм муки нужно взять 400 грамм, а вместо 4 яиц — 8 яиц.
Другой пример применения пропорции — решение задачи на уровне бытовых расчетов, например, при покупке товаров со скидкой. Если цена товара со скидкой известна, а нужно найти его первоначальную цену, можно использовать пропорцию. Зная, что товар был снижен в цене на 20%, можно рассчитать его первоначальную стоимость, используя пропорцию.
Цена товара со скидкойСкидкаПервоначальная цена
| 80 рублей | 20% | ? |
Применение пропорции в повседневной жизни помогает решать различные задачи и ситуации, связанные с соотношением между объектами или явлениями. Знание этого математического понятия позволяет легче ориентироваться в окружающем мире и применять его на практике.
Золотое сечение и его связь с пропорцией

Золотое сечение имеет много интересных свойств и применений в различных областях, включая математику, искусство, архитектуру и природу. Оно возникает в результате разделения отрезка на две части таким образом, что отношение длины всего отрезка к длине большей его части равно отношению длины большей части к длине меньшей. Математически это можно записать следующим образом:
φ = (a + b) / a = a / b
где a — большая часть отрезка, b — меньшая часть отрезка.
Связь золотого сечения с пропорцией заключается в том, что отношения длин отрезков в золотом сечении совпадают с отношениями в пропорции. Например, если отрезок AB делится в золотом сечении так, что отношение длины AB к длине большей части AC равно отношению длины большей части AC к длине меньшей части BC, то это можно записать в виде пропорции:
AB / AC = AC / BC
или
AB : AC = AC : BC
Таким образом, золотое сечение является одним из способов представления пропорции.
Золотое сечение имеет множество интересных свойств и применений и широко используется в искусстве и архитектуре для создания гармоничных и эстетически приятных пропорций. Оно также встречается в природе, например, в строении листьев, расположении семян в солнечных цветках и форме раковины улитки.
Золотое сечение и пропорция — важные понятия в математике, которые находят свое применение не только в учебных задачах, но и в реальной жизни и искусстве.
Практическое применение пропорции в архитектуре

Одно из применений пропорции в архитектуре — это установление соотношения между различными элементами здания или сооружения. Например, пропорциональное соотношение может быть использовано для определения высоты столбов или длины колонн в соответствии с общей высотой здания.
Пропорция также может быть применена для создания гармоничной композиции фасада здания. Архитекторы могут использовать золотое сечение или другие математические пропорции для расположения окон, дверей и других деталей фасада таким образом, чтобы они создавали эстетически приятное впечатление.
Кроме того, пропорция может быть использована для создания баланса и симметрии в архитектуре. Архитекторы могут использовать пропорциональные соотношения для распределения пространства и элементов в здании таким образом, чтобы сохранить его гармоничный вид.
Пропорция также играет важную роль в планировке городов. Архитекторы и градостроители могут использовать пропорциональные соотношения для определения размеров улиц, площадей и других общественных пространств, чтобы создать удобную и гармоничную среду для жителей.
Таким образом, пропорция играет важную роль в архитектуре, помогая архитекторам создавать гармоничные и эстетически приятные сооружения.
Вопрос-ответ:
Что такое пропорция?
Пропорция — это равенство двух отношений. В математике она используется для сравнения величин и построения соотношений между ними.
Как определить пропорцию в математике?
Пропорция состоит из четырех чисел, которые разделены на две пары. Если отношение первой пары равно отношению второй пары, то это пропорция.
Какие примеры пропорций можно привести?
Примерами пропорций могут быть: соотношение длин сторон подобных фигур, соотношение количества ингредиентов при готовке, соотношение скоростей движения и другие.
Как решать задачи на пропорцию?
Для решения задач на пропорцию необходимо сначала записать пропорцию, затем найти значение неизвестной величины, используя свойство равенства пропорций.
В чем практическое применение пропорций в повседневной жизни?
Пропорции широко используются в повседневной жизни, например, при расчете дозировки лекарств, при составлении рецептов, при определении соотношения смесей в химических реакциях и многих других сферах.



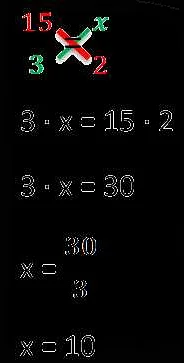
Пропорция в математике для 6 класса — это важное понятие, которое помогает нам решать различные задачи. Пропорция — это равенство двух отношений. Например, если у нас есть две пары чисел: 2 и 4, 6 и 12, то мы можем сказать, что они образуют пропорцию, так как отношение первой пары чисел (2/4) равно отношению второй пары чисел (6/12). Пропорция можно записать так: 2/4 = 6/12. Чтобы решать задачи с пропорциями, нужно уметь находить неизвестные значения. Например, если известно, что 2/4 = 6/12, мы можем найти неизвестное значение, например, x. Для этого нужно записать пропорцию в виде уравнения: 2/4 = x/12 и решить его. Зная, что 2/4 = 1/2, мы можем найти значение x: 1/2 = x/12, x = 6. Таким образом, пропорция помогает нам находить неизвестные значения, используя равенство отношений.
Пропорция в математике — это одно из основных понятий, которое поможет ученику в дальнейшем успешно решать задачи. Я очень рад, что в данной статье я нашел четкое определение и наглядные примеры, которые помогли мне лучше понять и запомнить это понятие. Пропорция — это равенство двух отношений. Это очень важно в практическом применении, например, при решении задач на пропорциональное деление. Я бы хотел поблагодарить авторов статьи за их труд и старания в изложении материала. Благодаря им, я легко освоил новую тему и готов к новым математическим вызовам.
Статья очень понятно и доступно объясняет, что такое пропорция в математике для учеников 6 класса. Я всегда слышала этот термин, но никогда не понимала его смысл. Теперь я поняла, что пропорция — это математическое соотношение, при котором два отношения равны между собой. Мне очень помогли примеры из статьи, особенно про разные пропорции с яблоками и бутербродами. Теперь я точно знаю, как применять пропорции в задачах и решать их. Очень хорошая статья для понимания математики! Большое спасибо автору!
Пропорция в математике – это очень важное понятие, которое помогает нам решать различные задачи. Я учусь в 6 классе, и недавно мы начали изучать эту тему. Пропорция – это равенство двух отношений. Например, если у нас есть две пары чисел, например, 2 и 4, 6 и 12, то мы можем сказать, что они образуют пропорцию, потому что отношение первого числа ко второму равно отношению третьего числа к четвертому. Вот такая простая и полезная штука! Мне нравится решать задачи с использованием пропорций, так как это помогает мне лучше понять отношения между числами. Например, мы можем использовать пропорцию для решения задачи о пропорциональном делении. Все это помогает мне развивать логическое мышление и улучшать свои навыки в математике.
Пропорция в математике — это важное понятие, с которым сталкиваются ученики 6 класса. Оно помогает понять взаимосвязь между различными числами и величинами. Пропорция состоит из двух дробей, и они равны между собой. Если в одной дроби числитель и знаменатель увеличиваются или уменьшаются в одно и то же число раз, то и в другой дроби они также должны увеличиваться или уменьшаться в том же отношении. Например, если в пропорции 1/2 = 3/6 умножить числитель и знаменатель на 2, получим 2/4 = 6/12, что также равно. Пропорции используются в различных ситуациях, например, для расчета скидок, решения задач по пропорциональности и многих других. Понимание пропорции поможет в дальнейшем учебном процессе и повысит математическую грамотность.