Правила по математике как найти неизвестное пропорции
Содержимое
- 1 Правила по математике как найти неизвестное пропорции
- 1.1 Понятие пропорции
- 1.2 Основные свойства пропорций
- 1.3 Как найти неизвестную пропорцию?
- 1.4 Методы решения пропорций
- 1.5 Примеры решения пропорций
- 1.6 Расширенные применения пропорций
- 1.7 Вопрос-ответ:
- 1.7.0.1 Как найти неизвестное значение в пропорции?
- 1.7.0.2 Как использовать правило трех пропорций для решения задач математики?
- 1.7.0.3 Какие примеры задач можно решить с помощью правила трех пропорций?
- 1.7.0.4 Какие еще методы можно использовать для решения задач на пропорциональность?
- 1.7.0.5 Как найти неизвестные пропорции?
- 1.7.0.6 Какие правила пропорциональности существуют?
- 1.7.0.7 Как использовать правила пропорциональности в решении задач по математике?
- 1.8 Практические задания с пропорциями
- 1.9 Видео по теме:
Узнайте, как использовать правила математики для нахождения неизвестных пропорций. Эта статья предлагает простые и понятные шаги, которые помогут вам решить любую задачу по поиску пропорций.
Математика – это наука, которая помогает нам понять мир вокруг нас, а также научиться решать различные задачи. Одной из важных тем в математике является работа с пропорциями. Пропорции позволяют нам находить неизвестные значения, используя уже известные. Это незаменимый инструмент как в повседневной жизни, так и в научных исследованиях.
Для того чтобы найти неизвестные пропорции, необходимо знать некоторые правила. Во-первых, пропорция состоит из четырех чисел, которые образуют две пары пропорциональных отношений. Во-вторых, определение пропорции позволяет нам установить равенство этих отношений. В-третьих, для нахождения неизвестных значений в пропорции можно использовать методы кросс-умножения и кросс-деления.
Например, если у нас есть пропорция a:b = c:d, и мы знаем значения a и b, но не знаем значения c и d, то мы можем найти эти значения, перекрестно умножив или перекрестно деля a и b на c или d. Таким образом, мы получим равенство a*d = b*c, которое позволяет нам найти значения c и d.
Для успешного решения пропорций необходимо хорошо знать основные правила и иметь навык работы с уравнениями. Правильное использование пропорций позволяет нам с легкостью находить неизвестные значения, что является важным навыком для решения различных задач в математике, физике, экономике и других науках.
Понятие пропорции
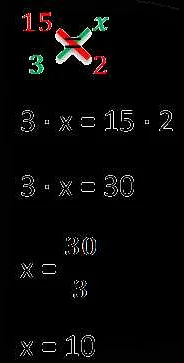
Пропорция записывается в виде a:b=c:d, где a и c — первый и третий члены, а b и d — второй и четвертый члены соответственно. При этом выполняется равенство отношений a/b=c/d.
Пропорцию можно представить в виде таблицы, где первая строка содержит значения первого и второго членов, а вторая строка — значения третьего и четвертого членов. Каждое значение стоит напротив соответствующего члена.
Пропорция может быть прямой или обратной. В прямой пропорции значения членов увеличиваются или уменьшаются одновременно, а в обратной пропорции значения членов изменяются в противоположных направлениях.
Пропорции широко применяются в различных областях, таких как физика, химия, экономика и строительство. Они помогают находить неизвестные значения на основе уже известных пропорций.
Основные свойства пропорций
Основные свойства пропорций:
СимволОписание
| А | Первое отношение |
| В | Второе отношение |
| С | Третье отношение |
| Д | Четвертое отношение |
Если пропорция А:В=С:Д верна, то можно вывести следующие свойства:
- При умножении или делении всех чисел пропорции на одно и то же число, пропорция остается равной.
- Если две пропорции равны, то их средние члены также равны.
- Если средние члены пропорции равны, то пропорция равна.
- Если две пропорции равны, то их внешние члены равны.
- Если внешние члены пропорции равны, то пропорция равна.
Знание основных свойств пропорций позволяет применять их при решении различных математических задач, в том числе для нахождения неизвестных пропорций.
Как найти неизвестную пропорцию?
Для решения задач по математике, связанных с пропорциями, иногда необходимо найти неизвестную пропорцию. Неизвестная пропорция может быть обозначена как x или y, и ее значение нужно найти с помощью известных пропорций и соотношений.
Чтобы найти неизвестную пропорцию, нужно использовать основные свойства пропорций. Пропорция — это равенство двух отношений, в котором каждое отношение имеет два числа, разделенных двоеточием. Например, a:b = c:d.
Для нахождения неизвестной пропорции, можно использовать методы перекрестного умножения или деления. Если известны три пропорции и одно отношение, можно использовать метод перекрестного умножения. Если известны две пропорции и одно отношение, можно использовать метод перекрестного деления.
Примеры:
- Дана пропорция a:b = c:d, и известно значение a. Чтобы найти неизвестную пропорцию c, нужно использовать формулу c = (d * a) / b.
- Дана пропорция a:b = c:d, и известно значение c. Чтобы найти неизвестную пропорцию d, нужно использовать формулу d = (b * c) / a.
Важно помнить, что при нахождении неизвестной пропорции нужно учитывать единицы измерения и сохранять их в результатах вычислений.
Зная правила по математике для нахождения неизвестной пропорции, можно решать разнообразные задачи, связанные с соотношениями и пропорциями. Эти навыки пригодятся не только в школе, но и в повседневной жизни, например, при расчетах в рецептах или планировании финансовых расходов.
Методы решения пропорций
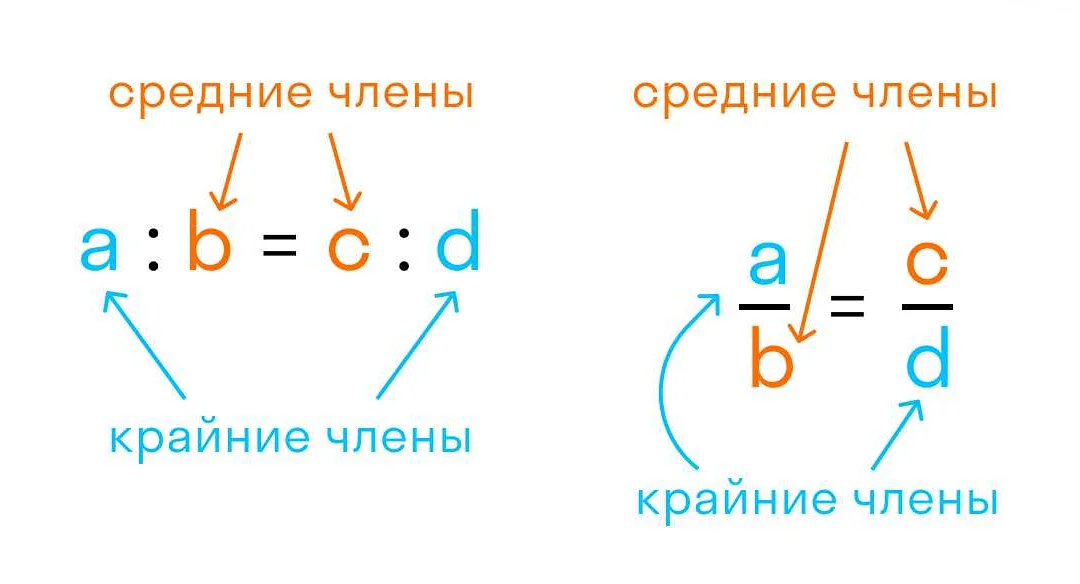
Для нахождения неизвестных пропорций можно использовать несколько методов:
- Метод умножения. Данный метод основан на свойстве пропорции, согласно которому произведение крайних членов равно произведению средних. Для решения пропорции по этому методу необходимо умножить крайние члены и приравнять их к произведению средних членов. Затем полученное уравнение можно решить и найти значение неизвестной пропорции.
- Метод деления. Этот метод основан на том же свойстве пропорции, но в данном случае используется деление. Для решения пропорции по этому методу необходимо разделить произведение крайних членов на один из средних членов и получить значение неизвестной пропорции.
- Метод перестановки. Данный метод применяется, когда изначально данные пропорции записаны в неправильной форме. При использовании этого метода необходимо переставить члены пропорции так, чтобы неизвестная пропорция была самостоятельно стоящим членом. Затем можно использовать один из предыдущих методов для решения пропорции.
Выбор метода решения пропорции зависит от конкретной задачи и предпочтения решающего. Важно помнить, что результаты полученные при решении пропорций должны быть проверены и соответствовать логическому смыслу задачи.
Примеры решения пропорций
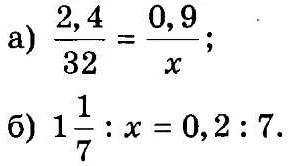
Вот несколько примеров решения пропорций:
- Найдем неизвестное значение в пропорции:
2/3 = x/9
Умножаем крест-на-крыж и получаем:
2 * 9 = 3 * x
18 = 3x
Разделим обе части на 3:
x = 6
Ответ: x = 6
- Рассмотрим следующую пропорцию:
5/8 = x/12
Применяем правило трех:
5 * 12 = 8 * x
60 = 8x
Разделим обе части на 8:
x = 7.5
Ответ: x = 7.5
Таким образом, пропорции могут быть решены путем установления соответствия между отношениями и применения правила трех для нахождения неизвестных значений.
Расширенные применения пропорций

- Решение задач на доли и проценты: С помощью пропорций можно решать задачи, связанные с расчетом долей и процентов. Например, можно использовать пропорцию для нахождения процента от числа или для расчета скидки на товар.
- Расчет скорости и времени: Пропорции можно применять для расчета скорости и времени пути. Например, если известна скорость и время движения, можно использовать пропорцию для расчета расстояния.
- Расчет площади и объема: Пропорции могут быть использованы для расчета площади и объема различных фигур. Например, с помощью пропорций можно рассчитать площадь треугольника или объем параллелепипеда.
- Решение задач на скорость и давление: Пропорции могут быть полезны при решении задач на скорость и давление. Например, можно использовать пропорцию для перевода единиц измерения скорости или для расчета давления в жидкости.
Расширенные применения пропорций демонстрируют важность умения применять их в различных ситуациях. Они помогают решать задачи, связанные с долями, процентами, скоростью, временем, площадью, объемом и другими величинами. Знание пропорций позволяет более эффективно анализировать и решать математические задачи, а также применять их в реальной жизни.
Вопрос-ответ:
Как найти неизвестное значение в пропорции?
Для нахождения неизвестного значения в пропорции нужно использовать правило трех пропорций, которое гласит: если две пропорции равны между собой, то их отношения также равны. Таким образом, для нахождения неизвестного значения нужно установить равенство двух пропорций и решить полученное уравнение.
Как использовать правило трех пропорций для решения задач математики?
Для использования правила трех пропорций для решения задач математики нужно воспользоваться следующим алгоритмом: 1) Сформулировать задачу и определить, какие значения известны, а какие неизвестны. 2) Установить равенство двух пропорций, где известные и неизвестные значения будут соответствовать соответствующим сторонам пропорции. 3) Решить полученное уравнение и найти неизвестное значение. 4) Проверить полученный ответ на соответствие условиям задачи.
Какие примеры задач можно решить с помощью правила трех пропорций?
С помощью правила трех пропорций можно решить различные задачи, такие как: 1) Нахождение неизвестной длины или высоты, используя известные пропорции и значения. 2) Расчет неизвестного времени или скорости на основе известных пропорций. 3) Определение неизвестного объема или площади с использованием известных пропорций и значений. 4) Решение задач на пропорциональность и соотношение различных величин.
Какие еще методы можно использовать для решения задач на пропорциональность?
Помимо правила трех пропорций, для решения задач на пропорциональность можно использовать следующие методы: 1) Метод подобных треугольников, основанный на свойствах подобных фигур. 2) Метод сравнения долей, когда необходимо сравнить доли различных величин. 3) Метод перевода величин в одну и ту же единицу измерения, чтобы сравнить их непосредственно. 4) Метод пропорциональной арифметики, использующий правила арифметики для решения пропорциональных задач.
Как найти неизвестные пропорции?
Для того чтобы найти неизвестные пропорции, нужно использовать правила пропорциональности. Если у нас есть две пары чисел, которые образуют пропорцию, то можно найти значение неизвестного числа, используя формулу пропорции. Например, если у нас есть пропорция a/b = c/d, то мы можем найти значение любой из переменных, если знаем значения трех других. Для этого нужно перемножить числа по диагонали и приравнять полученные произведения.
Какие правила пропорциональности существуют?
Существуют несколько правил пропорциональности. Одно из них — правило трех пропорций. Если у нас есть три пропорции a/b = c/d = e/f, то можно найти значение любой из переменных, используя формулу пропорции. Другое правило — правило обратно пропорциональных величин. Если у нас есть две пропорции a/b = c/d и b/e = d/f, то можно найти значение неизвестной переменной, используя формулу пропорции. Еще одно правило — правило пропорций суммы и разности. Если у нас есть пропорции a/b = c/d и b+d/a-c = e/f, то можно найти значение неизвестных переменных, используя формулу пропорции.
Как использовать правила пропорциональности в решении задач по математике?
Чтобы использовать правила пропорциональности в решении задач по математике, нужно внимательно прочитать условие задачи и выделить заданные и неизвестные величины. Затем нужно определить, какие из правил пропорциональности можно применить, и записать соответствующую пропорцию. После этого можно решить пропорцию, используя формулу пропорции, и найти значение неизвестной величины. Важно помнить, что при решении задач по пропорциям нужно быть внимательным и аккуратным, чтобы не допустить ошибок.
Практические задания с пропорциями
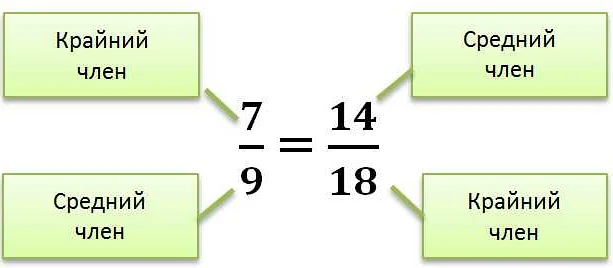
Давайте рассмотрим несколько практических заданий, чтобы лучше понять, как работать с пропорциями:
-
- Задание 1: Если 3 пачки муки стоят 150 рублей, сколько стоит 5 таких пачек муки?
Для решения этой задачи можно использовать пропорцию:
-
-
- 3 пачки муки = 150 рублей
- 5 пачек муки = ?
-
Применяя правило трех, можно записать следующее уравнение:
3/5 = 150/х, где х — неизвестная цена 5 пачек муки.
Решая это уравнение, можно найти цену 5 пачек муки.
-
- Задание 2: Если 4 работника могут выполнить работу за 6 дней, сколько дней потребуется 8 работникам?
Для решения этой задачи можно использовать пропорцию:
-
-
- 4 работника = 6 дней
- 8 работников = ?
-
Применяя правило трех, можно записать следующее уравнение:
4/8 = 6/х, где х — неизвестное количество дней, необходимых 8 работникам.
Решая это уравнение, можно найти количество дней, необходимых 8 работникам.
-
- Задание 3: Если 2 машины смогут проехать 360 километров, сколько километров смогут проехать 5 таких машин?
Для решения этой задачи можно использовать пропорцию:
-
-
- 2 машины = 360 километров
- 5 машин = ?
-
Применяя правило трех, можно записать следующее уравнение:
2/5 = 360/х, где х — неизвестное количество километров, которое смогут проехать 5 машин.
Решая это уравнение, можно найти количество километров, которое смогут проехать 5 машин.
Таким образом, решение задач с пропорциями поможет вам находить неизвестные значения на основе известных данных и применять математические навыки в практических ситуациях.
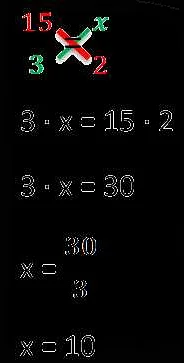



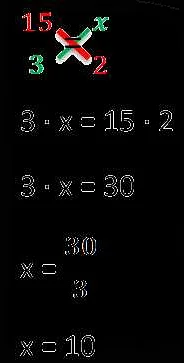
Статья очень полезная и информативная! Я всегда испытывал трудности в понимании пропорций, но благодаря этой статье моя путаница исчезла. Теперь я знаю, как правильно решать задачи с неизвестными пропорциями. Особенно мне понравилось объяснение о том, как использовать правило трех. Теперь я могу легко рассчитать неизвестные значения, используя пропорции. Это очень удобно и экономит время при решении математических задач. Большое спасибо автору за такую понятную и доходчивую статью! Я рекомендую ее всем, кто хочет научиться работать с пропорциями без проблем.
Отличная статья! Я всегда сталкиваюсь с проблемой решения пропорций в математике и никак не мог понять, как это делается. Но благодаря вашим правилам, мне стало намного проще разобраться с этой темой. Теперь я понимаю, что для нахождения неизвестных пропорций нужно использовать правило трех и применять его к задачам разного уровня сложности. Я также узнал, что существует несколько методов решения пропорций, и важно выбрать наиболее подходящий в каждой конкретной ситуации. Ваша статья действительно помогла мне освоить эту тему и повысить свои навыки в математике. Большое спасибо!
Отличная статья! Я всегда сталкиваюсь с проблемой нахождения неизвестных пропорций в математике, и эти правила очень помогли мне разобраться. Я часто использовал метод подобия треугольников, но теперь я понял, что есть и другие способы. Особенно мне понравилось, как объясняют правило трёх пропорций. Когда я стал применять это правило на практике, я удивился, насколько легко можно решить даже сложные задачи. Теперь я с уверенностью могу решать задачи с неизвестными пропорциями и помогать своим детям в учебе. Спасибо за полезную информацию! Жду с нетерпением следующих статей на эту тему.
Отличная статья! Математика всегда была моей слабой стороной, особенно когда речь заходит о пропорциях. Но благодаря этим правилам, я чувствую, что могу легче разобраться в этой теме. Всегда было сложно понять, как найти пропорцию, когда известны только часть данных. Теперь я понимаю, что нужно использовать правило трех, чтобы найти неизвестные значения. Очень полезно знать, что пропорция — это просто равенство двух отношений и что можно использовать крест-произведение для нахождения неизвестных значений. Я также узнала о методе использования процентов для решения пропорций. Эти правила помогут мне не только в школе, но и в повседневной жизни, например, при покупке товаров со скидкой. Очень благодарна за эти полезные советы!