Что такое простые числа в математике 6

Простые числа в математике 6 — это числа, которые имеют только два делителя: 1 и само число. Они являются основой для множества математических концепций и алгоритмов. Узнайте, как определить простое число и какие интересные свойства они имеют.

Простыми числами называются натуральные числа, которые имеют ровно два различных делителя: единицу и само число. В отличие от составных чисел, которые имеют больше двух делителей, простые числа обладают рядом уникальных свойств и являются важным объектом изучения в математике.

Простые числа представляют собой основу для многих алгоритмов и методов в криптографии и информационной безопасности. Их свойства используются для шифрования данных и создания надежных алгоритмов проверки простоты чисел. Особенности простых чисел играют важную роль в различных областях математики и науки в целом.

«Простыми числами называются числа, которые не могут быть разложены на множители, кроме как на единицу и само число. Простые числа являются фундаментальными строительными блоками в теории чисел и имеют множество интересных и необычных свойств.»

Узнать, является ли число простым, не всегда просто. Несмотря на то, что простые числа легко распознаются, их распределение в натуральном ряду не подчиняется простым правилам. Они встречаются редко и несистематично, что делает их изучение интересным и сложным одновременно.

Числа, которые нельзя разложить на множители

В математике существуют числа, которые нельзя представить в виде произведения других чисел, кроме как самого числа и единицы. Такие числа называются простыми числами или простыми числами.

Простые числа имеют только два делителя: 1 и само число. Например, числа 2, 3, 5, 7, 11 и т. д. являются простыми числами. Если число можно разложить на множители, то оно называется составным числом.

Простые числа играют важную роль в различных областях математики и науки. Они используются в криптографии, где большие простые числа используются для защиты информации. Простые числа также используются в алгоритмах, шифрах и в теории чисел.

Важно отметить, что существует бесконечное количество простых чисел. Это было доказано еще в древности греческим математиком Евклидом. Он предложил метод, известный как «доказательство от противного», чтобы показать, что существует бесконечное количество простых чисел.

Простые числа имеют множество интересных свойств и характеристик, которые исследуются математиками на протяжении веков. Изучение простых чисел является важной и увлекательной областью математики, которая имеет широкий спектр применений и приложений.

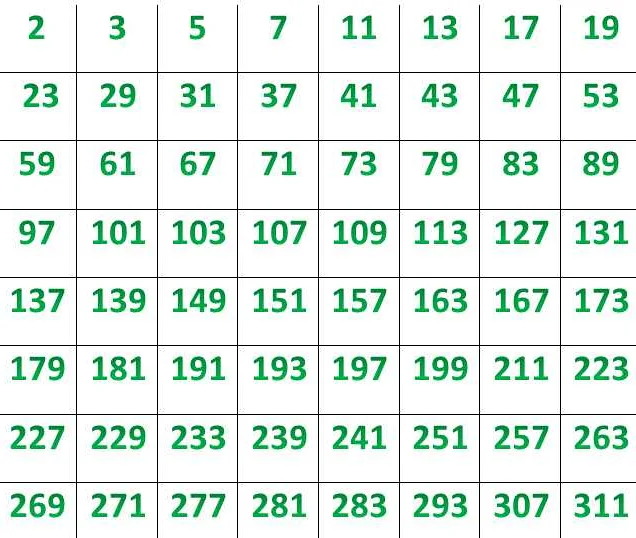
Определение простых чисел

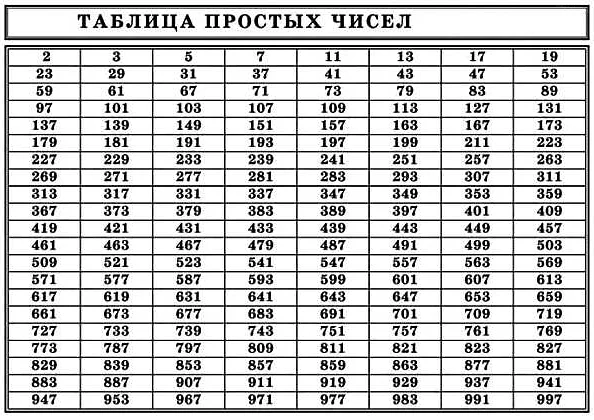
Простые числа являются основными строительными блоками для всех других чисел. Их уникальные свойства и особенности делают их важными для математических исследований и различных приложений в науке и технологиях.

Например, простые числа широко применяются в криптографии для создания безопасных алгоритмов шифрования. Они также играют важную роль в решении задач в комбинаторике, теории чисел и других областях математики.

Существует бесконечное количество простых чисел, но они распределены неравномерно и становятся все более редкими с увеличением значения числа.

Некоторые из известных простых чисел: 2, 3, 5, 7, 11, 13, 17 и так далее.

Простые числаДелители

2	1, 2
3	1, 3
5	1, 5
7	1, 7

Свойства простых чисел

Основные свойства простых чисел:

1. Бесконечность: простых чисел бесконечное множество. Это означает, что независимо от того, сколько простых чисел уже известно, всегда можно найти еще одно простое число, которое больше любого известного.
2. Единственность: каждое натуральное число больше 1 может быть разложено на простые множители с единственным образом. Это называется основной теоремой арифметики. Например, число 12 может быть разложено на простые множители 2, 2 и 3.
3. Плотность: простые числа распределены равномерно на числовой прямой. Между любыми двумя простыми числами всегда можно найти хотя бы одно другое число. Это свойство называется плотностью простых чисел.
4. Неразложимость: простые числа не могут быть разложены на меньшие простые множители. Например, число 5 не может быть разложено на более маленькие простые числа.

Изучение свойств простых чисел играет важную роль в различных областях математики и находит применение в криптографии, теории чисел, алгоритмах и других дисциплинах.

Существование бесконечного множества простых чисел

Важным свойством простых чисел является их бесконечность. Это означает, что существует бесконечное множество простых чисел. Это утверждение было доказано великим древнегреческим математиком Евклидом около 300 года до н.э. В своей работе «Начала» Евклид предложил конструктивное доказательство этого факта.

Доказательство заключается в предположении, что существует только конечное число простых чисел, и затем строится новое число, которое является произведением всех этих простых чисел, увеличенное на 1. Это новое число либо само является простым, либо имеет делитель, который не может быть одним из предыдущих простых чисел. Таким образом, возникает противоречие и предположение о конечности простых чисел оказывается неверным.

Доказательство Евклида является классическим и приводит к выводу, что существует бесконечное количество простых чисел. Это важное свойство простых чисел широко используется в различных областях математики и имеет множество практических применений.

Примеры простых чисел:

2

3

5

7

11

Разложение числа на простые множители

Простые числа являются основными строительными блоками всех натуральных чисел. Они не имеют делителей, кроме себя самого и единицы. Примерами простых чисел являются 2, 3, 5, 7, 11 и т.д.

Разложение числа на простые множители происходит путем деления заданного числа на наименьший простой множитель. Если число делится без остатка, то это число является одним из простых множителей. Затем процесс повторяется для полученного частного до тех пор, пока не достигнется 1.

Наиболее распространенным способом разложения числа на простые множители является использование древа разложения. Каждое простое число, найденное при делении, становится вершиной древа, а его потомки — результаты деления.

Пример разложения числа 60 на простые множители:

• 60 -> 2 * 30
• 30 -> 2 * 15
• 15 -> 3 * 5

Таким образом, разложение числа 60 на простые множители будет выглядеть следующим образом: 2 * 2 * 3 * 5.

Разложение числа на простые множители помогает в решении различных задач, таких как нахождение наибольшего общего делителя, нахождение наименьшего общего кратного и т.д.

Проверка числа на простоту

Существуют различные способы проверки числа на простоту. Один из наиболее простых и распространенных способов — это метод перебора делителей.

Для проверки числа на простоту, необходимо последовательно проверить все числа от 2 до n-1, где n — проверяемое число. Если найдется хотя бы один делитель, отличный от 1 и самого числа n, то число n не является простым. В противном случае, число n является простым.

Например, чтобы проверить число 13 на простоту, мы последовательно проверим делители 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Ни одно из этих чисел не является делителем 13, поэтому 13 является простым числом.

При проверке чисел на простоту можно также использовать математические алгоритмы, например, алгоритмы проверки на простоту Миллера-Рабина или тест Ферма.

Важно отметить, что проверка числа на простоту может быть трудоемкой задачей, особенно при работе с большими числами. Поэтому существуют специальные алгоритмы и методы проверки чисел на простоту с использованием компьютеров.

Проверка числа на простоту является важной задачей в различных областях науки и техники, таких как криптография, теория чисел, компьютерная безопасность и другие.

Простые числа в криптографии

Простые числа играют важную роль в криптографии, науке, которая занимается защитой информации. Криптография используется для шифрования сообщений и обеспечения безопасности в интернете, электронной коммерции и других областях.

Одно из основных применений простых чисел в криптографии — это создание криптографических ключей. Криптографический ключ представляет собой случайное простое число, которое используется для шифрования и дешифрования сообщений. Криптосистемы, основанные на простых числах, обладают высокой стойкостью к взлому и являются основой современной криптографии.

Простые числа также используются в алгоритмах электронной подписи. Электронная подпись позволяет проверить подлинность и целостность электронного документа. Для создания электронной подписи используется закрытый ключ, который является простым числом. Закрытый ключ подписывает документ, а открытый ключ, который также является простым числом, позволяет проверить подпись.

Простые числа также применяются в алгоритмах генерации случайных чисел. Генерация случайных чисел играет важную роль в криптографии, поскольку случайность является ключевым фактором для создания безопасных криптографических ключей.

Простые числа в криптографии являются основой безопасности и обеспечивают защиту информации. Использование простых чисел позволяет создавать криптосистемы, которые трудно взломать и обеспечивают конфиденциальность и целостность данных.

Вопрос-ответ:

Что такое простые числа?

Простые числа — это натуральные числа, большие единицы, которые имеют только два делителя: единицу и само число. Они не делятся на другие натуральные числа.

Как определить, является ли число простым?

Существует несколько способов определить, является ли число простым. Один из них — проверить его на делимость на все числа от 2 до квадратного корня из этого числа. Если ни одно из этих чисел не делит заданное число без остатка, то оно является простым.

Сколько простых чисел существует?

Простых чисел бесконечно много. Существует бесконечное количество натуральных чисел, и среди них всегда можно найти новое простое число.

Какие свойства имеют простые числа?

Простые числа обладают несколькими важными свойствами. Например, любое натуральное число можно представить в виде произведения простых чисел, называемое его простым разложением. Также, простые числа играют важную роль в криптографии и теории чисел.

Интересные факты о простых числах

1. Простые числа не могут быть представлены как произведение двух меньших чисел, кроме как 1 и самого себя. Например, число 7 является простым, потому что его можно разделить только на 1 и 7.

2. Бесконечное количество простых чисел. Это утверждение было доказано древнегреческим математиком Евклидом более 2000 лет назад.

3. Простые числа можно использовать для шифрования данных. Алгоритм RSA, широко используемый для безопасной передачи информации в интернете, основан на сложности факторизации больших простых чисел.

4. Самое большое известное простое число на данный момент имеет более 24 миллионов цифр. Оно было найдено в 2018 году и имеет название M77232917.

5. Простые числа имеют множество интересных свойств и встречаются во многих областях науки, включая физику, компьютерные науки и криптографию.

Простые числа продолжают оставаться объектом активных исследований, и многие из их свойств до сих пор не полностью поняты. Их важность и значимость в математике и смежных областях делает их захватывающим объектом изучения.

Видео по теме: