Что такое составное и простое число в математике

Составные и простые числа в математике — это основные понятия, которые помогают классифицировать числа. Составные числа могут быть разложены на множители, в то время как простые числа имеют только два множителя — 1 и само число. Узнайте больше о различиях между составными и простыми числами и как они используются в математике.

В математике существуют два основных типа чисел — составные и простые числа. Понимание разницы между ними является важным аспектом для понимания основных математических концепций и применения их в практических задачах.

Простое число — это натуральное число, большее 1, которое не может быть разделено на другие натуральные числа, кроме себя самого и 1. Простые числа имеют только два делителя — 1 и само число. Например, числа 2, 3, 5, 7 и 11 являются простыми числами.

Составное число, напротив, может быть разделено на более чем два натуральных делителя. Другими словами, составное число — это натуральное число, которое может быть разложено на более мелкие множители. Например, число 4 является составным, так как его можно разделить на 2 и 2.

Простые числа играют важную роль в математике и криптографии. Они используются для создания шифров и алгоритмов, обеспечивающих безопасность информации. Знание простых чисел и их свойств позволяет исследовать различные аспекты числовой теории и применять их в разных областях науки и технологий.

Составное число в математике: основные понятия и определения

В математике существуют два основных типа чисел: простые и составные. В данном разделе мы рассмотрим составные числа и их основные понятия и определения.

Составное число — это натуральное число, которое имеет более двух делителей. Другими словами, это число, которое можно разделить на два или более числа, отличных от 1 и самого числа.

Например, число 6 является составным, так как оно может быть разделено на 2 и 3. В то же время, число 7 является простым, потому что его единственные делители — это 1 и само число 7.

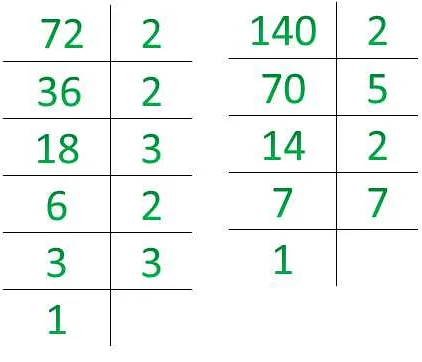
Составные числа можно выразить в виде произведения их простых множителей. Например, число 12 можно представить как 2 * 2 * 3, где 2 и 3 — простые числа. Такое представление называется факторизацией.

Для определения, является ли число составным, можно применить методы проверки на простоту, такие как деление на все числа от 2 до квадратного корня из этого числа. Если ни одно из этих чисел не является делителем, то число является простым. В противном случае, число считается составным.

Составные числа имеют свои свойства и особенности, и изучение их играет важную роль в алгебре и теории чисел. Они используются, например, в криптографии для создания безопасных шифров и в различных алгоритмах и вычислениях.

Что такое составное число и как его определить?

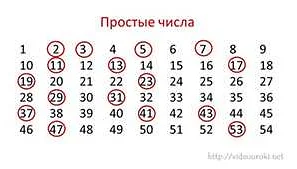
Чтобы определить, является ли число составным, необходимо проверить, есть ли у него делители, кроме 1 и самого числа. Для этого можно последовательно делить число на все натуральные числа, начиная с 2, и проверять, делится ли оно нацело. Если оно делится нацело хотя бы на одно число, отличное от 1 и самого числа, то оно составное. Если же число не делится нацело ни на одно число, то оно простое.

Например, число 12 является составным, потому что оно делится нацело на 2, 3, 4 и 6. А число 7 является простым, потому что оно не делится нацело ни на одно число, кроме 1 и самого себя.

Как вычислить делители составного числа?

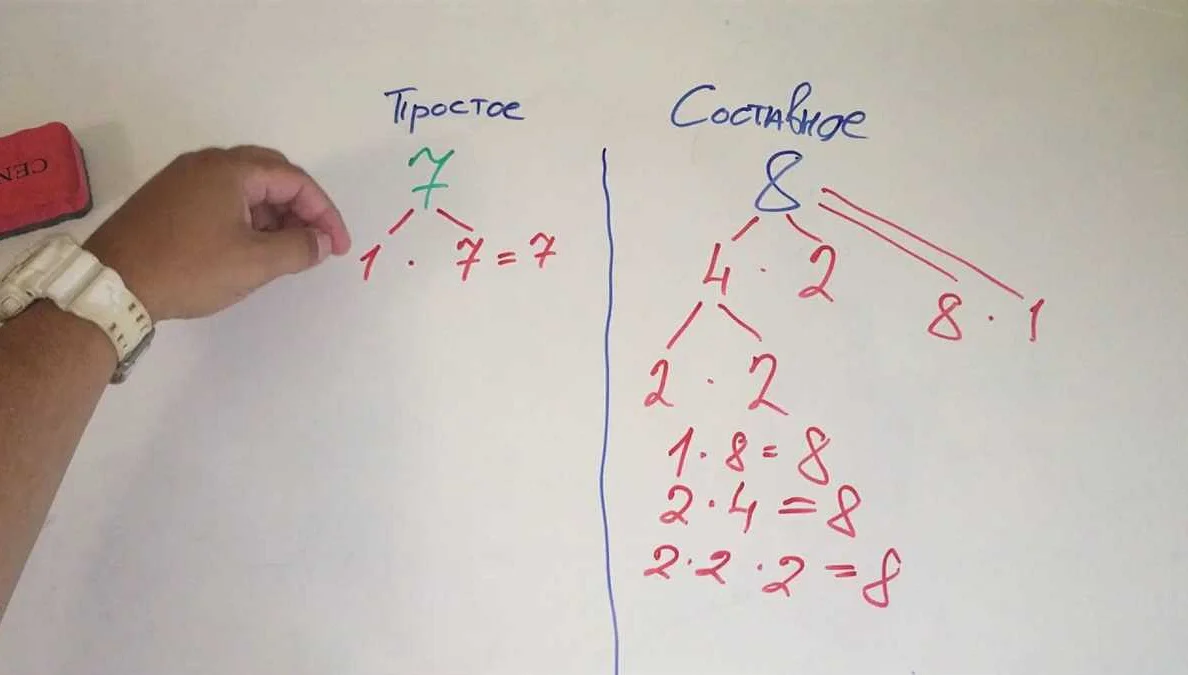
1. Найдите все простые числа, которые меньше или равны заданному составному числу.
2. Проверьте каждое из найденных простых чисел на деление заданного составного числа без остатка.
3. Если простое число является делителем, добавьте его в список делителей.

Например, для вычисления всех делителей числа 12:

Найдем все простые числа, которые меньше или равны 12: 2, 3, 5, 7, 11.

Проверим каждое простое число на деление числа 12: 2 делится на 12 без остатка, 3 делится на 12 без остатка.

Таким образом, делители числа 12: 1, 2, 3, 4, 6, 12.

Заметим, что 1 и само число также являются делителями любого числа, поэтому они всегда включаются в список делителей.

Используя описанный метод, можно вычислить все делители любого составного числа.

Простое число: особенности и основные свойства

Основным свойством простых чисел является их бесконечность. Постулат Евклида утверждает, что существует бесконечное количество простых чисел. Это значит, что независимо от того, какое большое простое число мы найдем, всегда можно найти еще большее.

Простые числа играют важную роль в различных областях математики и криптографии. Они используются для шифрования информации, создания безопасных ключей и доказательства сложности алгоритмов.

Для определения, является ли число простым или нет, существует несколько методов. Наиболее простой способ — это проверка делителей числа. Если число имеет делители, отличные от 1 и самого себя, то оно является составным, а не простым.

Простые числа имеют много интересных свойств и особенностей, которые продолжают изучаться и исследоваться учеными. Их характеристики и взаимоотношения с другими числами являются объектом интереса исследователей математики и теории чисел.

Простые числа имеют важное место в математике и являются одними из самых основных и фундаментальных объектов изучения. Их свойства и особенности продолжают удивлять и вдохновлять ученых по всему миру.

Что такое простое число и как его отличить от составного?

Составные числа — это натуральные числа, больше 1, которые имеют более двух делителей. Иными словами, составное число можно разложить на более чем два множителя. Например, число 6 является составным, потому что оно делится на 2 и 3.

Отличить простое число от составного можно следующим образом:

1. Проверка на делимость: если число делится без остатка на любое число, кроме 1 и самого себя, то оно является составным.
2. Проверка на простоту: если число не делится без остатка ни на одно число, кроме 1 и самого себя, то оно является простым.

Таким образом, чтобы определить, является ли число простым или составным, необходимо проверить его на делимость всеми числами в диапазоне от 2 до корня из этого числа. Если число делится без остатка хотя бы на одно число из этого диапазона, то оно составное, в противном случае — простое.

Какие числа являются простыми?

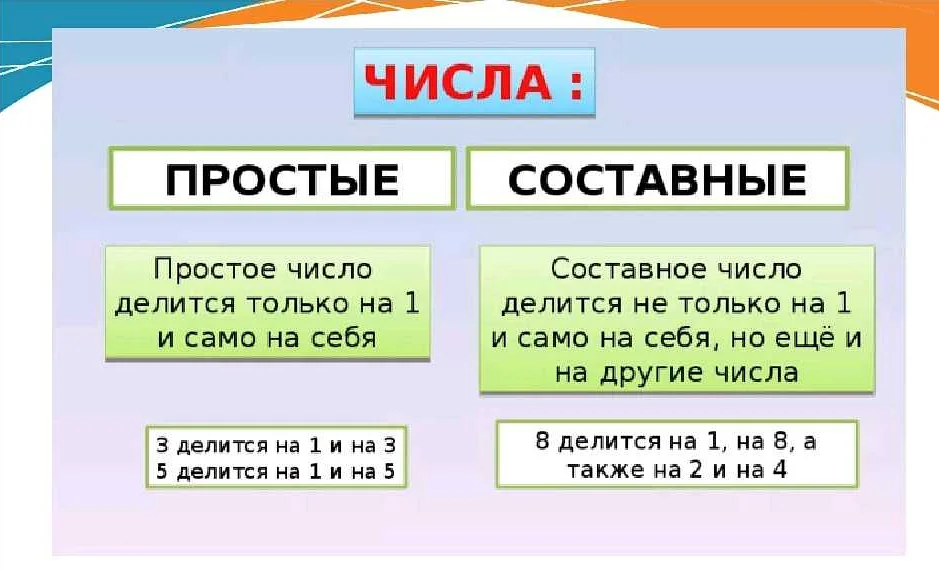
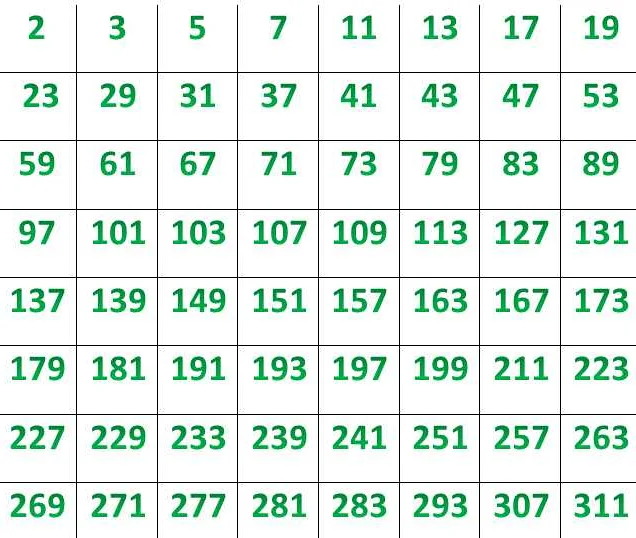
Например, числа 2, 3, 5, 7, 11, 13 и т.д. являются простыми, потому что они имеют только два делителя — единицу и само число.

Простые числа имеют важное значение в математике и криптографии. Они используются для построения шифров и алгоритмов, которые обеспечивают безопасность в интернете.

Сравнение составных и простых чисел: основные различия

Простые числа — это натуральные числа, которые имеют только два делителя: 1 и само число. Простые числа нельзя разложить на простые множители, за исключением самих себя.

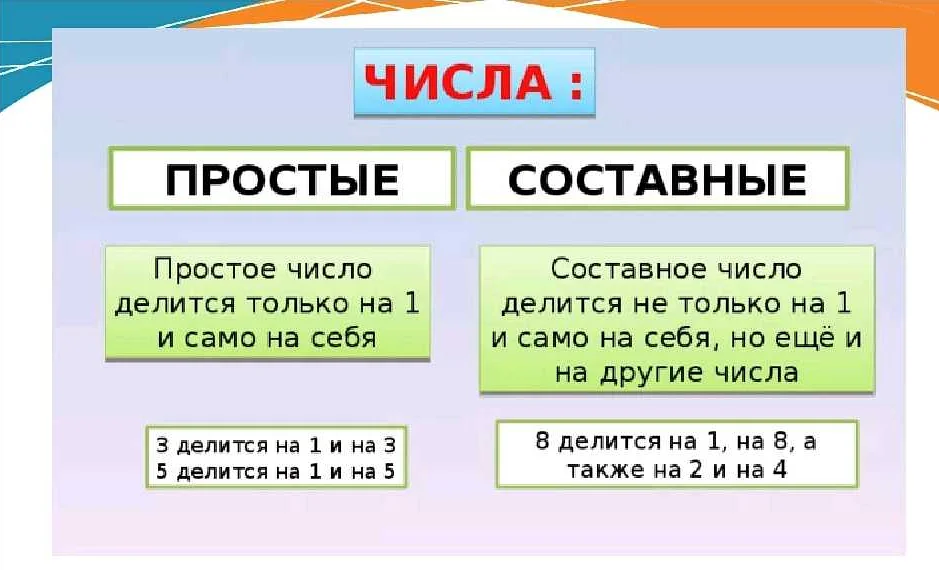
Основные различия между составными и простыми числами:

1. Количество делителей:

• Составные числа имеют более двух делителей.
• Простые числа имеют только два делителя: 1 и само число.

2. Разложение на простые множители:

• Составные числа можно разложить на простые множители.
• Простые числа нельзя разложить на простые множители, за исключением самих себя.

3. Примеры:

• Составные числа: 4 (2 * 2), 6 (2 * 3), 8 (2 * 2 * 2).
• Простые числа: 2, 3, 5, 7, 11.

Знание о составных и простых числах важно в различных областях математики, таких как криптография и теория чисел. Составные числа могут быть разложены на простые множители, что помогает в их анализе и решении различных задач.

Как отличить составное число от простого?

Для того чтобы определить, является ли число простым или составным, можно использовать несколько методов. Вот некоторые из них:

1. Проверка делителей: Если число имеет делитель, отличный от 1 и самого себя, то оно является составным. Делители числа можно найти путем последовательной проверки всех чисел, начиная с 2 и заканчивая корнем из числа. Если найден делитель, то число является составным, иначе — простым.
2. Проверка по формуле: Некоторые числа имеют специальные формулы, которые позволяют легко определить их простоту или составность. Например, числа, оканчивающиеся на 0, 2, 4, 6 или 8, всегда являются составными.
3. Тест Миллера-Рабина: Этот тест является вероятностным и используется для определения простоты числа. Он основан на теории чисел и выполняет несколько итераций, проверяя случайные числа на условия простоты. Если число проходит все итерации, то оно с большой вероятностью является простым.
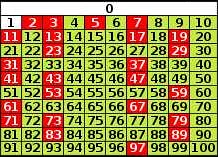
4. Решето Эратосфена: Этот метод использует алгоритм для нахождения всех простых чисел до заданного числа. Путем исключения всех чисел, которые являются делителями числа, можно определить его простоту или составность.

Использование одного или нескольких из этих методов может помочь в определении, является ли число простым или составным.

Какова роль составных и простых чисел в математике?

Простые числа — это числа, которые имеют только два делителя: 1 и само число. Они не могут быть разложены на более мелкие множители. Простые числа являются строительными блоками для других чисел и являются основой многих математических теорий и алгоритмов. Простые числа используются в криптографии для защиты информации и в различных математических задачах для выявления закономерностей.

Примеры простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 и т.д.

Составные числа — это числа, которые имеют более двух делителей. Они могут быть разложены на простые множители. Составные числа играют важную роль в алгоритмах и криптографии и используются для решения сложных математических задач.

Примеры составных чисел: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18 и т.д.

Изучение составных и простых чисел позволяет математикам понять множество закономерностей и свойств чисел, а также разрабатывать новые алгоритмы и методы решения задач. Эти числа являются фундаментальными в математике и находят применение в различных областях знаний.

Видео по теме:

Что такое составное число?

Составное число — это натуральное число, которое имеет больше двух делителей, кроме единицы и самого себя. Другими словами, составное число можно разложить на простые множители.

А что такое простое число?

Простое число — это натуральное число, которое имеет ровно два делителя: единицу и само себя. Простые числа нельзя разложить на простые множители, поэтому они не имеют других делителей.

Какие примеры составных чисел можно привести?

Некоторые примеры составных чисел: 4, 6, 8, 9, 10 и т.д. Все эти числа имеют делители помимо единицы и самих себя. Например, число 8 можно разделить на 2 и 4.

А какие числа являются простыми?

Некоторые примеры простых чисел: 2, 3, 5, 7, 11 и т.д. Эти числа имеют только два делителя: единицу и себя само. Например, число 7 нельзя разделить на другие числа без остатка.

Что такое простое число?

Простое число — это натуральное число, которое имеет ровно два делителя: 1 и само себя. Например, числа 2, 3, 5, 7, 11 и так далее являются простыми числами.

Что такое составное число?

Составное число — это натуральное число, которое имеет больше двух делителей. Другими словами, это число можно представить в виде произведения двух или более чисел, отличных от 1 и самого числа. Например, число 4 является составным, так как оно может быть представлено как 2 * 2.