Что называется пружинным и математическим маятником
Содержимое
- 1 Что называется пружинным и математическим маятником
Узнайте, что такое пружинный и математический маятник, и как они работают. Узнайте о законе Гука и формулах, используемых для вычисления периода колебаний. Познакомьтесь с применением маятников в различных областях, от физики до часового дела.
Пружинный маятник – это устройство, использующее пружину для создания колебаний. Принцип работы пружинного маятника основан на законе Гука, согласно которому сила, действующая на пружину, пропорциональна ее деформации. Когда пружина растягивается или сжимается, возникает возвратная сила, которая возвращает пружину в исходное положение.
Пружинные маятники широко используются в различных устройствах, включая часы, подвесные мосты и автомобильные подвески. Они также являются основой для изучения осцилляций и колебаний в физике.
Математический маятник – это абстрактная модель, представляющая собой точку массы, подвешенную на нерастяжимой и невесомой нити. Он не имеет физической формы и используется для исследования законов движения и колебаний. Математический маятник идеализирован и не учитывает воздействие сопротивления среды и других факторов, которые могут влиять на его движение.
Основное отличие между пружинным и математическим маятниками состоит в их принципах работы. Пружинный маятник основывается на законе Гука и использует пружину для создания колебаний. Математический маятник моделирует колебания точки массы на нити и учитывает только влияние силы тяжести и длины нити на его движение. Благодаря своей простоте и идеализированности, математический маятник является полезным инструментом для изучения и применения законов физики.
Определение понятий
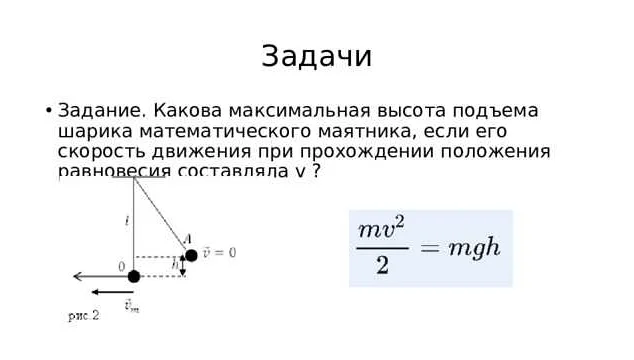
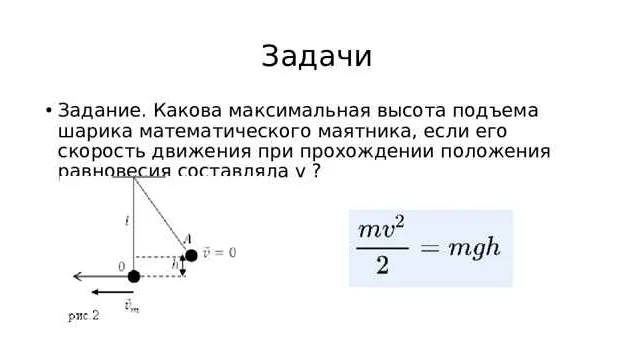
Математический маятник – это идеализированная модель физической системы, состоящая из точки, называемой массой, и невесомой нерастяжимой нитью или стержнем, на котором эта точка подвешена. Основной принцип работы математического маятника заключается в колебаниях, которые возникают из-за взаимодействия массы точки с гравитационной силой.
Таким образом, основное отличие между пружинным и математическим маятниками заключается в составе физической системы и механизме возникновения колебаний. Принцип работы пружинного маятника основан на взаимодействии массы груза с пружиной, а принцип работы математического маятника основан на взаимодействии массы точки с гравитационной силой.
Видео по теме:
Принцип работы пружинного маятника
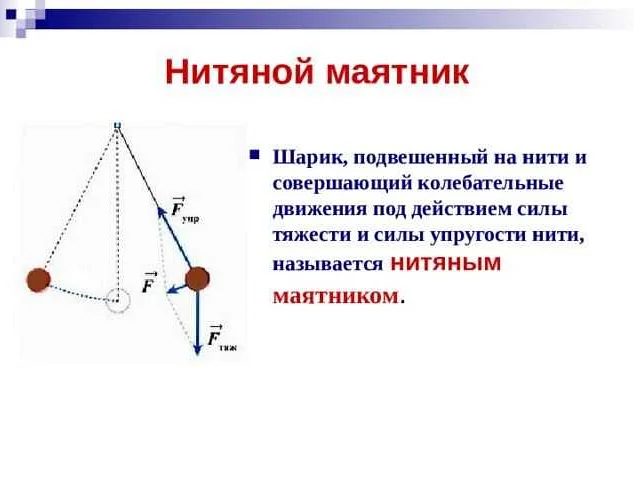
Принцип работы пружинного маятника основан на законе Гука, который утверждает, что сила, с которой пружина действует на груз, пропорциональна его смещению относительно равновесной позиции и направлена в противоположную сторону. Это значит, что если груз отклоняется от своего равновесного положения, пружина будет действовать на него силой, направленной в противоположную сторону, чтобы вернуть его к равновесию.
Когда груз движется вверх или вниз, пружина растягивается или сжимается. В результате возникает упругая потенциальная энергия, которая превращается в кинетическую энергию, когда груз проходит через равновесную позицию. После этого процесс повторяется в обратном направлении.
Принцип работы пружинного маятника заключается в том, что пружина действует как упругий элемент, который позволяет грузу совершать колебания между двумя крайними точками. Это создает регулярные и повторяющиеся движения, которые используются, например, в часах с маятником или амортизаторах автомобилей.
Пружинные маятники обладают своими особенностями и характеристиками, которые могут быть определены математически. Они важны для понимания и анализа работы таких устройств, а также для разработки новых технологий и улучшения существующих.
Принцип работы математического маятника
Принцип работы математического маятника основан на законах физики и математики. Когда маятник отклоняется от своего положения равновесия, возникают колебания. Эти колебания можно описать математическими формулами, такими как уравнение маятника.
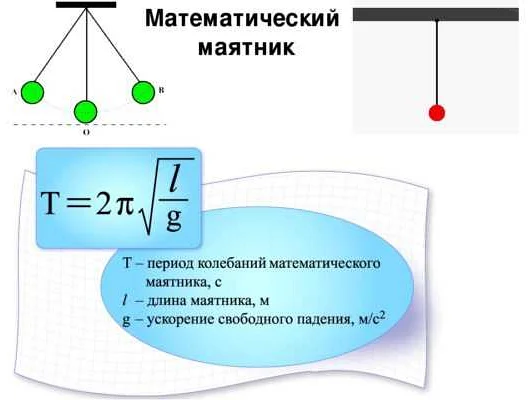
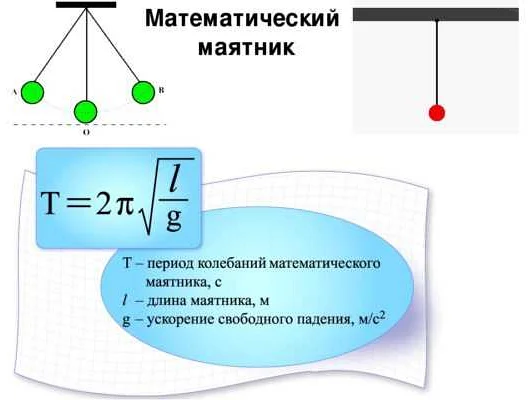
Уравнение маятника позволяет рассчитать период колебаний – время, за которое маятник совершает одну полную качку вперед и назад. Формула для расчета периода колебаний математического маятника выглядит следующим образом:
ФормулаОписание
| T = 2π√(L/g) | Период колебаний (T) зависит от длины стержня (L) и ускорения свободного падения (g). |
Здесь π (пи) – математическая константа, а √(L/g) – квадратный корень из отношения длины стержня к ускорению свободного падения.
Математический маятник является абстрактной моделью, которая позволяет ученым и студентам исследовать законы колебаний и их взаимосвязь с другими физическими явлениями. Он широко используется в учебных целях и научных исследованиях для изучения основ механики и математики.
Отличия в уравнениях движения
Тип маятникаУравнение движения
| Пружинный маятник | Уравнение движения пружинного маятника может быть представлено в виде: |
| m * x» + k * x = 0 | |
| где m — масса маятника, x» — ускорение маятника, k — жесткость пружины, x — смещение маятника от положения равновесия. | |
| Математический маятник | Уравнение движения математического маятника может быть представлено в виде: |
| θ» + g * sin(θ) = 0 | |
| где θ» — угловое ускорение маятника, g — ускорение свободного падения, θ — угол отклонения маятника от вертикали. |
Таким образом, уравнения движения пружинного и математического маятников отличаются как по своей форме, так и по входящим в них переменным. Знание этих уравнений позволяет более полно понять принципы работы и особенности движения каждого из этих типов маятников.
Различия в поведении системы

Пружинный и математический маятники имеют некоторые важные различия в своем поведении.
Пружинный маятник, как следует из его названия, основан на использовании пружины. Из-за этого он обладает свойством упругости и может колебаться вокруг равновесного положения. Пружинный маятник может иметь как гармонические, так и апериодические колебания в зависимости от системы пружин и масс, которые в него входят.
Математический маятник, в отличие от пружинного, основан на использовании математического описания движения. Он представляет собой точечную массу, подвешенную на невесомой нерастяжимой нити. Математический маятник колеблется с постоянной периодичностью и амплитудой, независимо от массы точечной массы и длины нити.
Таким образом, пружинный маятник имеет более сложное поведение, так как его колебания зависят от параметров пружины и массы, в то время как математический маятник имеет более предсказуемое и упрощенное движение.
Примеры использования

Пружинные и математические маятники имеют широкий спектр применений в различных областях, включая физику, инженерию и науку.
- В физике пружинные маятники используются для изучения колебаний и силы упругости. Они помогают определить законы Гука и изучаются в курсе механики.
- Математические маятники используются для моделирования математических функций и конкретных проблем, например, в физике колебаний. Они позволяют наглядно представить абстрактные понятия и облегчают понимание математических законов.
- В инженерии пружинные маятники применяются для тестирования долговечности и прочности различных конструкций. Они помогают определить границы допустимых нагрузок и предсказать поведение системы при различных условиях.
- Математические маятники используются в научных исследованиях, например, для моделирования колебаний планет и других небесных тел. Они помогают установить закономерности и предсказать будущие события в космосе.
Таким образом, пружинные и математические маятники являются важными инструментами для изучения различных явлений и разработки новых технологий. Их применение охватывает широкий спектр областей и способствует расширению нашего понимания мира.
Применение в научных исследованиях
В физике пружинный и математический маятники используются для изучения основных законов движения и колебаний. Они позволяют проводить эксперименты и измерять параметры, такие как период колебаний, амплитуда и частота. Эти данные затем анализируются и используются для проверки теоретических моделей и уравнений.
Инженеры используют пружинные и математические маятники для изучения различных динамических систем и определения их характеристик. Например, они могут быть использованы для оценки жесткости материалов, испытания устойчивости конструкций или определения параметров силы удара.
В астрономии пружинные и математические маятники могут быть использованы для изучения колебаний и периодических процессов в космических системах. Они помогают ученым лучше понять движение планет и спутников, а также предсказывать их будущие положения и характеристики.
Примеры научных исследованийОбласть применения
| Изучение зависимости периода колебаний пружинного маятника от его массы и жесткости пружины | Физика |
| Определение амплитуды и частоты колебаний математического маятника в зависимости от его длины | Физика |
| Исследование динамической устойчивости здания при различных условиях нагрузки | Инженерия |
| Оценка динамических свойств материала при различных температурах и давлениях | Инженерия |
| Анализ колебаний спутников вокруг планеты и определение их орбит и характеристик | Астрономия |
Таким образом, пружинные и математические маятники играют важную роль в научных исследованиях, позволяя ученым изучать различные явления и процессы, а также разрабатывать новые теории и модели.
Выводы
Пружинный маятник представляет собой систему, состоящую из пружины и точечной массы, которая движется вдоль оси пружины. При этом, пружина испытывает упругую деформацию, и движение массы происходит с изменяющейся скоростью и ускорением.
Математический маятник — это система, состоящая из невесомой нитью и точечной массы, которая движется по кривой линии. В данном случае, масса движется под действием силы тяжести, и ее движение описывается математическими уравнениями.
Таким образом, пружинный и математический маятники обладают своими особенностями и применяются в различных областях науки и техники. Пружинные маятники используются, например, в часах с подвесными пружинными маятниками, а математические маятники — в физических экспериментах и в научных исследованиях.
Вопрос-ответ:
Как работает пружинный маятник?
Пружинный маятник — это устройство, в котором движение происходит за счет действия силы упругости пружины. Когда пружина растягивается или сжимается, она накапливает потенциальную энергию, которая превращается в кинетическую энергию при возвращении пружины в исходное положение. Этот процесс повторяется с определенной частотой, образуя колебания.
Чем отличается пружинный маятник от математического?
Основное отличие между пружинным и математическим маятниками заключается в принципе работы. Пружинный маятник использует силу упругости пружины для создания колебаний, в то время как математический маятник основан на законах гравитации и использует массу и длину подвеса для создания периодического движения.
Какие принципиальные различия в поведении пружинного и математического маятников?
Пружинный маятник обладает линейной зависимостью между силой упругости пружины и ее деформацией, что означает, что сила упругости пружины пропорциональна ее удлинению или сжатию. В математическом маятнике, сила гравитации играет определяющую роль, и его движение описывается с помощью уравнения математического маятника.
В чем применение пружинного маятника?
Пружинные маятники находят широкое применение в различных областях, включая физику, механику и инженерию. Они используются для измерения силы упругости материалов, определения их жесткости, исследования колебаний и резонанса, а также для создания устройств, таких как метрономы и часы.
Что такое период колебаний в пружинном маятнике?
Период колебаний в пружинном маятнике — это время, за которое он совершает одно полное колебание — от исходного положения до максимального вытяжения, обратного движения и возвращения в исходное положение. Этот период зависит от массы пружины, силы упругости и массы, подвешенной к пружине.
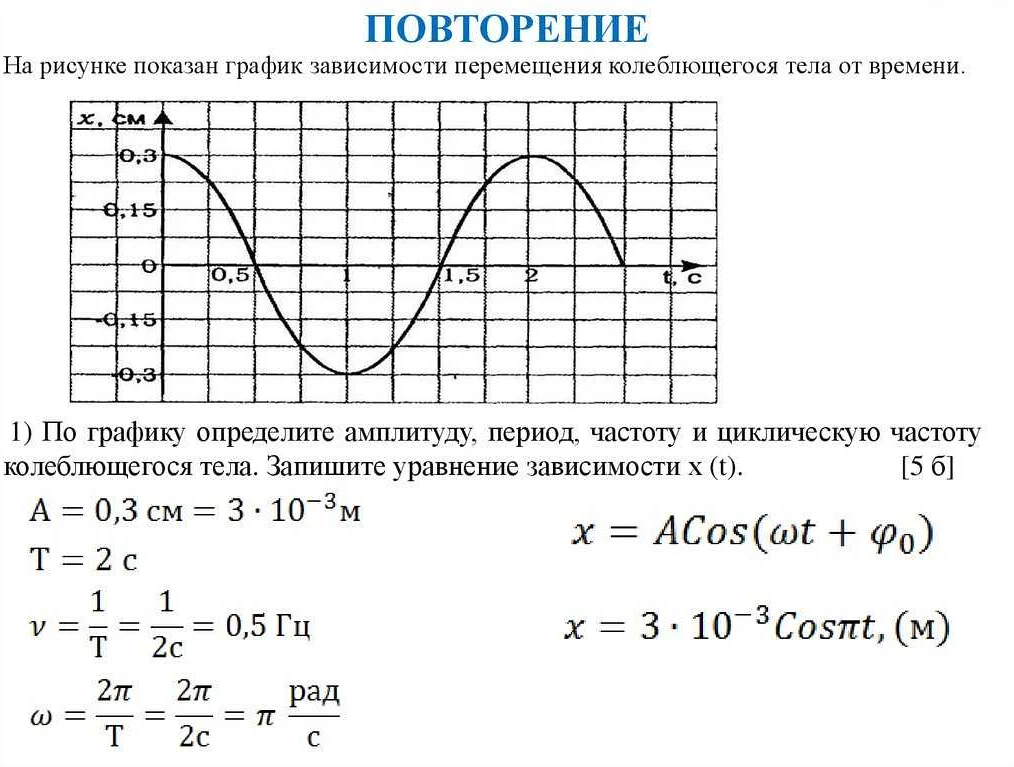

Статья очень интересная и понятная. Я никогда не задумывалась о том, что пружинный и математический маятники отличаются друг от друга. Оказывается, пружинный маятник основывается на законе Гука, а математический маятник — на математических уравнениях. Я с удовольствием узнала, что пружинный маятник используется во многих сферах, например, в автоиндустрии и строительстве. А математический маятник помогает в изучении физики и математики. Благодаря этой статье я поняла, что оба маятника имеют свои преимущества и применение. Спасибо за такую интересную информацию! Желаю автору продолжать писать такие полезные статьи.