Математика 6 класс что такое круг

Узнайте, что такое круг в математике 6 класса. Узнайте его основные свойства и формулы, а также как решать задачи, связанные с кругом.

Круг — это геометрическая фигура, которая является одной из основных фигур в математике. Он определяется как множество точек, которые находятся на одинаковом расстоянии от определенной точки, называемой центром круга. Расстояние от центра круга до любой точки на его окружности называется радиусом круга.

Круг имеет множество свойств, которые делают его уникальным. Одно из главных свойств круга — равенство всех радиусов. Это значит, что все отрезки, соединяющие центр круга с точками на его окружности, имеют одинаковую длину. Также круг обладает свойством транзитивности, то есть если два круга имеют одинаковый радиус, то они равны.

Круг является важной фигурой в геометрии и имеет множество приложений в повседневной жизни. Он используется в архитектуре, дизайне, инженерии и других областях. Например, круг используется для построения колеса, тарелки, круглых столов и многих других предметов.

Круг в математике

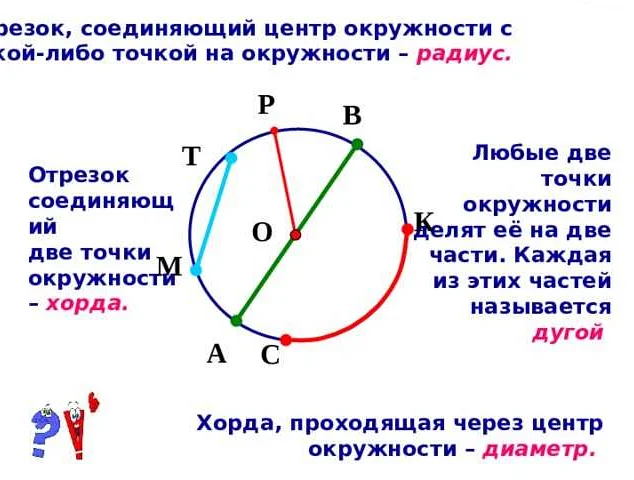
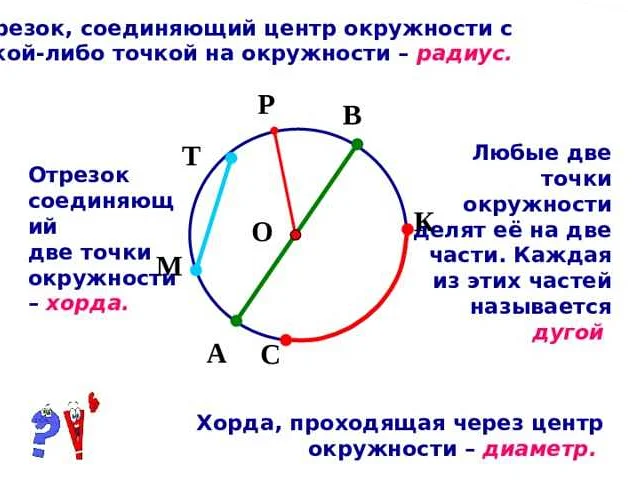
Основными характеристиками круга являются его радиус, диаметр и окружность. Радиус – это расстояние от центра круга до любой точки на его окружности. Диаметр – это отрезок, соединяющий две точки на окружности, проходящий через ее центр. Окружность – замкнутая кривая, состоящая из всех точек, находящихся на одном и том же расстоянии от центра круга.

Круг также имеет несколько важных свойств. Например, сумма длин дуг любых двух частей окружности, образованных внутри круга при пересечении его диаметра, всегда равна длине окружности. Площадь круга можно вычислить по формуле S = π * r^2, где S – площадь круга, π (пи) – математическая константа, приближенное значение которой равно 3,14, а r – радиус круга.

Круги широко используются в реальном мире, например, для описания формы колес, тарелок, монет и других предметов. Они также играют важную роль в физике, географии и других науках.

Изучение круга позволяет учащимся развивать понятия о геометрических фигурах, научиться вычислять их характеристики и применять их в реальном мире. Знание о круге также полезно для понимания более сложных концепций в математике и других науках.

Видео по теме:

Свойства круга

• Круг имеет только один радиус, который является постоянной величиной и равен расстоянию от центра круга до любой точки на его окружности.
• Диаметр круга — это отрезок, соединяющий две точки на окружности, проходящие через центр круга. Диаметр равен удвоенному радиусу.
• Окружность — это граница круга, представляющая собой замкнутую кривую, состоящую из всех точек, находящихся на одинаковом расстоянии от центра круга.
• Площадь круга — это мера площади, ограниченной окружностью. Площадь круга можно вычислить по формуле: S = π * r², где S — площадь, π — число пи (примерно 3,14), r — радиус.
• Длина окружности — это длина границы круга. Длину окружности можно вычислить по формуле: L = 2πr, где L — длина окружности, π — число пи (примерно 3,14), r — радиус.

Знание свойств круга позволяет проводить различные геометрические вычисления и применять их в практических задачах.

Диаметр круга

Длину диаметра круга обозначают буквой d. Она является удвоенной длиной радиуса: d = 2r, где r — радиус круга.

Диаметр круга также является основной характеристикой при решении задач, связанных с окружностями. Например, для нахождения площади круга и его длины (периметра) часто используется значение диаметра.

Зная диаметр круга, можно также найти его площадь и длину окружности. Площадь круга вычисляется по формуле S = πr², где π (пи) — математическая константа, примерное значение которой равно 3,14. Длина окружности определяется формулой C = πd, где d — диаметр круга.

Таким образом, диаметр круга играет важную роль в геометрии и позволяет решать различные задачи, связанные с окружностями.

Вопрос-ответ:

Какой радиус у круга?

Радиусом круга называется отрезок, соединяющий центр круга с любой точкой его окружности.

Как вычислить длину окружности?

Длина окружности равна произведению диаметра на число π (пи). Формула: L = π * d, где L — длина окружности, d — диаметр окружности.

Как найти площадь круга?

Площадь круга можно найти по формуле: S = π * (r^2), где S — площадь круга, r — радиус круга.

Какие свойства имеет круг?

У круга есть несколько свойств: все точки на окружности равноудалены от центра круга; длина любой хорды (отрезка, соединяющего две точки на окружности) равна диаметру; сумма углов, заключенных внутри круга, равна 360 градусов.

Радиус круга

Зная радиус круга, можно вычислить его диаметр, площадь и длину окружности. Диаметр круга равен удвоенному значению радиуса: d = 2r. Площадь круга можно найти по формуле: S = πr^2, где π (пи) — это математическая константа, примерное значение которой равно 3,14. Длина окружности круга вычисляется по формуле: L = 2πr.

Знание радиуса круга позволяет решать различные задачи, связанные с этой геометрической фигурой, такие как определение площади газона, вычисление длины траектории движения по круговому треку, нахождение расстояния между двумя точками на окружности и другие.

Формулы для вычисления параметров круга

Радиус круга (R) – это расстояние от центра круга до любой его точки. Для вычисления площади круга используется следующая формула:

S = π * R^2

где π – математическая константа, приближенное значение которой равно 3,14.

Для вычисления длины окружности круга используется следующая формула:

C = 2 * π * R

где C – длина окружности.

Также можно вычислить диаметр круга (D), который равен удвоенному значению радиуса:

D = 2 * R

Эти формулы помогают определить основные параметры круга и использовать их для решения различных задач в математике.

Формула для длины окружности

Если известен радиус окружности (r), то формула для вычисления длины окружности (L) выглядит так:

L = 2 * π * r

где π (пи) — это математическая константа, которая равна примерно 3,14159. Она используется для приближенного вычисления длины окружности.

Если известен диаметр окружности (d), то формула для вычисления длины окружности (L) выглядит так:

L = π * d

Также можно выразить диаметр через радиус:

d = 2 * r

Таким образом, формула для вычисления длины окружности через радиус может быть записана и так:

L = π * (2 * r)

Используя эти формулы, можно легко вычислить длину окружности для заданного радиуса или диаметра.

Формула для площади круга

Площадь круга можно вычислить по формуле:

S = π * r^2

где S — площадь круга, π — математическая константа, которая примерно равна 3,14, r — радиус круга.

Для расчета площади круга необходимо умножить квадрат радиуса на значение π.

Например, если радиус круга равен 5 см, то площадь круга будет:

S = 3,14 * 5^2 = 3,14 * 25 = 78,5 см^2.

Таким образом, формула позволяет легко и точно вычислить площадь круга по его радиусу.

Практическое применение круга

Круг имеет множество практических применений в различных сферах нашей жизни. Рассмотрим некоторые из них:

1. Геометрия: Круг является одной из основных геометрических фигур. Он применяется при решении различных геометрических задач, например, при вычислении площади круга, длины окружности, радиуса или диаметра.
2. Физика: Круг используется в физике для изучения различных явлений, таких как центростремительное ускорение и вращательное движение. Он также применяется при расчете площади сечения круглых объектов, например, труб и кабелей.
3. Инженерия: Круг широко используется в инженерии при проектировании и изготовлении различных конструкций. Он является основой для создания колес, шестеренок и других вращающихся деталей.
4. Архитектура: Круг применяется в архитектуре для создания куполов, арок и других круглых элементов зданий.
5. Медицина: Круг используется в медицине для изучения и описания форм органов и тканей человека. Он также применяется при проведении различных медицинских процедур, например, при ультразвуковом исследовании.

Это лишь некоторые примеры практического применения круга. В реальной жизни мы встречаемся с кругами повсюду и часто даже не задумываемся об их важности и значении. Знание свойств и особенностей круга позволяет нам лучше понимать окружающий мир и применять его в различных областях нашей жизни.

Круг в геометрии

Основные элементы круга:

• Центр круга — это точка, от которой все остальные точки находятся на одинаковом расстоянии.
• Радиус круга — это расстояние от центра круга до любой другой точки на окружности круга.
• Диаметр круга — это отрезок, соединяющий две точки на окружности круга и проходящий через центр круга. Диаметр равен удвоенному значению радиуса.
• Окружность круга — это линия, состоящая из всех точек находящихся на одинаковом расстоянии от центра круга.

Круг имеет много интересных свойств и характеристик, которые могут быть использованы в различных областях математики и реальной жизни.

Круг в физике

Круг играет важную роль в оптике. Он используется для описания световых волн и их распространения. Например, когда свет распространяется от точечного источника, он образует круглые световые пятна на экране или на другой поверхности. Круг также используется для определения фокусного расстояния линзы или зеркала.

Круг в физике также может означать закономерность или цикличность. Например, в газовых или жидких потоках может возникать круговое движение, называемое циркуляцией. Круговое движение также может быть наблюдено в электрических цепях или в магнитном поле.

Таким образом, понятие круга в физике имеет широкий спектр значений и применений, связанных с геометрией, оптикой и динамикой различных физических процессов.