Радиус что это такое в математике

Радиус – это важное понятие в математике, которое используется для определения расстояния от центра до точки на окружности или сфере. Узнайте, как вычислять радиус и его свойства в этой статье.

Радиус – одно из важнейших понятий, которое широко используется в математике. Радиусом называется расстояние от центра до любой точки окружности или сферы. Это фундаментальное понятие, которое используется во многих областях математики, включая геометрию, тригонометрию, алгебру и анализ.

Определение радиуса очень простое – это отрезок, соединяющий центр окружности или сферы с любой ее точкой. Радиус обычно обозначается буквой «r» или «R» и имеет единицу измерения длины, такую как метр, сантиметр, дюйм и т.д. Радиус также может быть отрицательным числом, если направление измерения идет в противоположную сторону от центра.

Примеры использования радиуса в математике весьма разнообразны. В геометрии радиус используется для вычисления площади и длины окружности, а также для определения других характеристик фигур, таких как объем и площадь сферы. В тригонометрии радиус применяется для определения тригонометрических функций, таких как синус, косинус и тангенс, а также для нахождения значений углов. В алгебре радиус используется при решении уравнений и систем уравнений. В анализе радиус применяется для определения границы сходимости рядов и рядов Тейлора. Это лишь некоторые примеры применения радиуса, и его роль в математике трудно переоценить.

Радиус: что это такое?

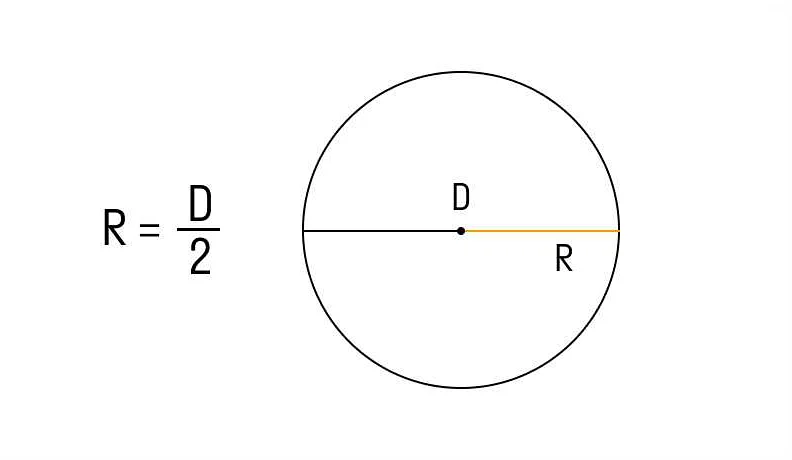
В геометрии радиус обычно обозначается символом r и используется для определения размеров фигур. Например, радиус окружности определяет ее размеры и форму, а также позволяет вычислять длину окружности, площадь и другие параметры.

В алгебре радиус часто используется в уравнениях и формулах, связанных с геометрическими объектами. Например, радиус вектор определяет положение точки в пространстве, а радиус-векторное уравнение задает уравнение окружности или сферы.

Радиус имеет важное значение не только в математике, но и в других науках и технических областях. Он используется в физике для определения размеров и формы объектов, в геодезии для измерения расстояний, в строительстве для проектирования и расчета конструкций и т.д.

В заключение, радиус — это ключевой параметр, который помогает определить размеры и форму геометрических объектов, а также использовать их в различных научных и технических приложениях.

Определение радиуса

Радиус обозначается обычно буквой r или R и измеряется в единицах длины.

Радиус окружности определяет длину отрезка, соединяющего центр окружности с ее любой точкой на поверхности. Радиус сферы определяет длину отрезка, соединяющего центр сферы с любой точкой на ее поверхности.

Зная радиус окружности, можно вычислить площадь и длину окружности, используя соответствующие формулы. Радиус сферы также используется для вычисления площади и объема сферы.

Радиус имеет множество применений в геометрии, физике, астрономии и других областях науки. Например, радиус используется для определения расстояний, построения графиков и моделей, а также для анализа и изучения различных объектов и явлений.

Радиус и геометрия

Зная длину радиуса окружности, мы можем рассчитать ее площадь и длину окружности с помощью соответствующих формул. Радиус также определяет расстояние от центра окружности до ее точек, а также углы, которые образуются между радиусами и хордами окружности.

В геометрии радиус шара также играет важную роль. Он определяет размер и форму шара, а также его объем и площадь поверхности. Зная радиус шара, мы можем рассчитать его объем и площадь поверхности с помощью соответствующих формул.

Радиус также является основным элементом при решении различных геометрических задач. Например, для построения окружности, мы можем использовать центр и радиус в качестве исходных данных. Также радиус позволяет нам определить, находится ли точка внутри окружности или вне ее, а также определить, пересекаются ли окружности или нет.

Радиус имеет широкое применение в различных областях геометрии и математики. Он является основным понятием в изучении окружностей, шаров, сфер, а также в решении задач на планиметрии и пространственной геометрии.

Радиус и окружность

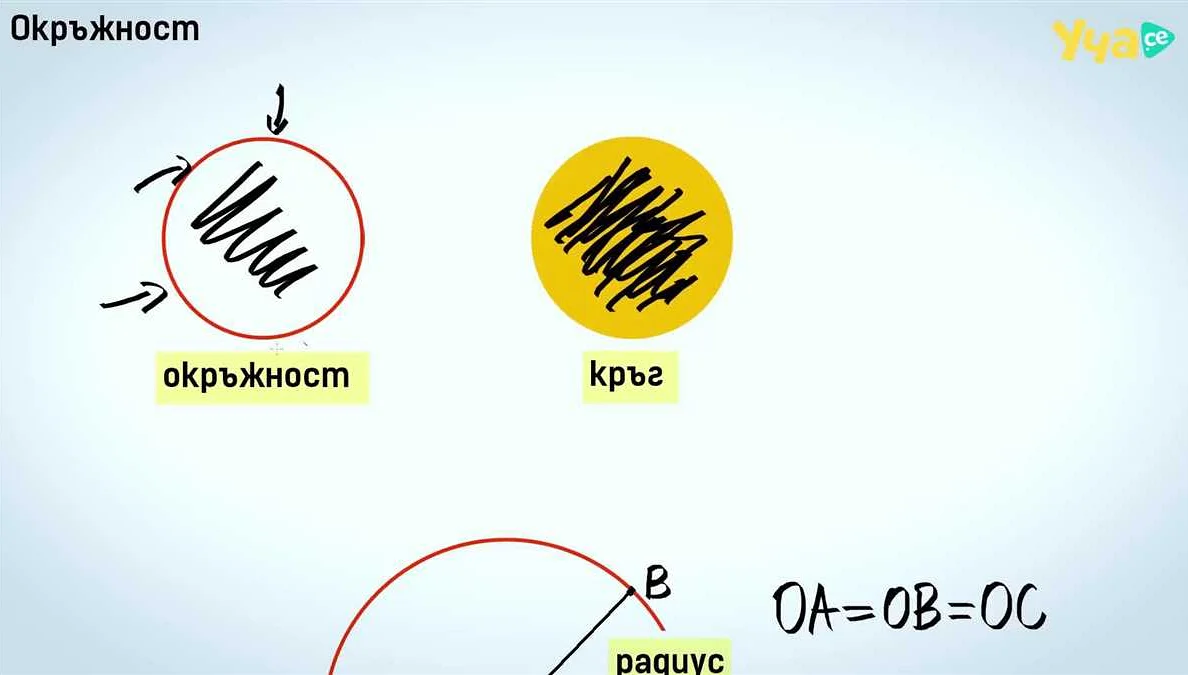
Окружность — это геометрическая фигура, состоящая из всех точек, которые находятся на одинаковом расстоянии от определенной точки, называемой центром окружности. Радиус является ключевым параметром для описания и измерения окружности.

Радиус окружности можно обозначить символом r или R. Он определяет размер окружности и связан с ее длиной, диаметром и площадью.

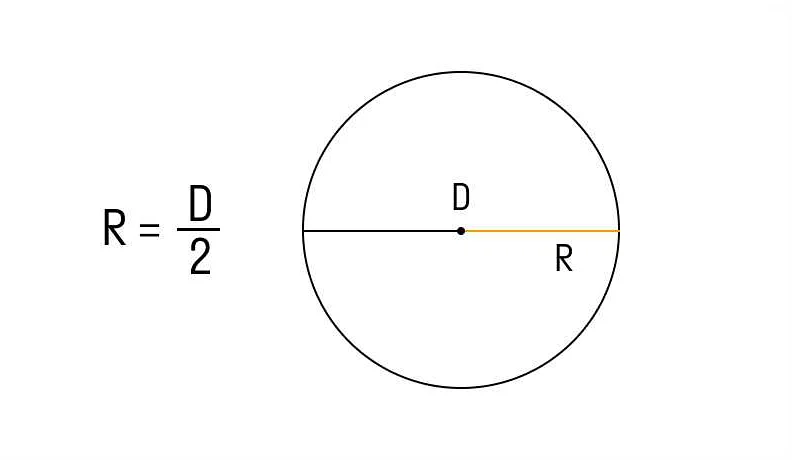
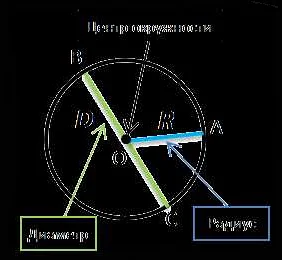
Диаметр — это отрезок, проходящий через центр окружности и соединяющий две ее точки. Диаметр равен удвоенному значению радиуса.

Длина окружности вычисляется по формуле L = 2πr, где π (пи) — это математическая постоянная, приближенное значение которой равно 3,14159.

Площадь окружности вычисляется по формуле S = πr^2, где ^2 обозначает возведение в квадрат.

Знание радиуса окружности позволяет решать различные задачи, связанные с геометрией и конструированием. Например, радиус используется для определения площади и длины окружности, а также для построения графиков и моделей.

Важно помнить, что радиус окружности всегда положительный и не может быть отрицательным или равным нулю. Окружность с радиусом равным нулю является точкой, а окружность с отрицательным радиусом не имеет геометрического смысла.

Радиус и сфера

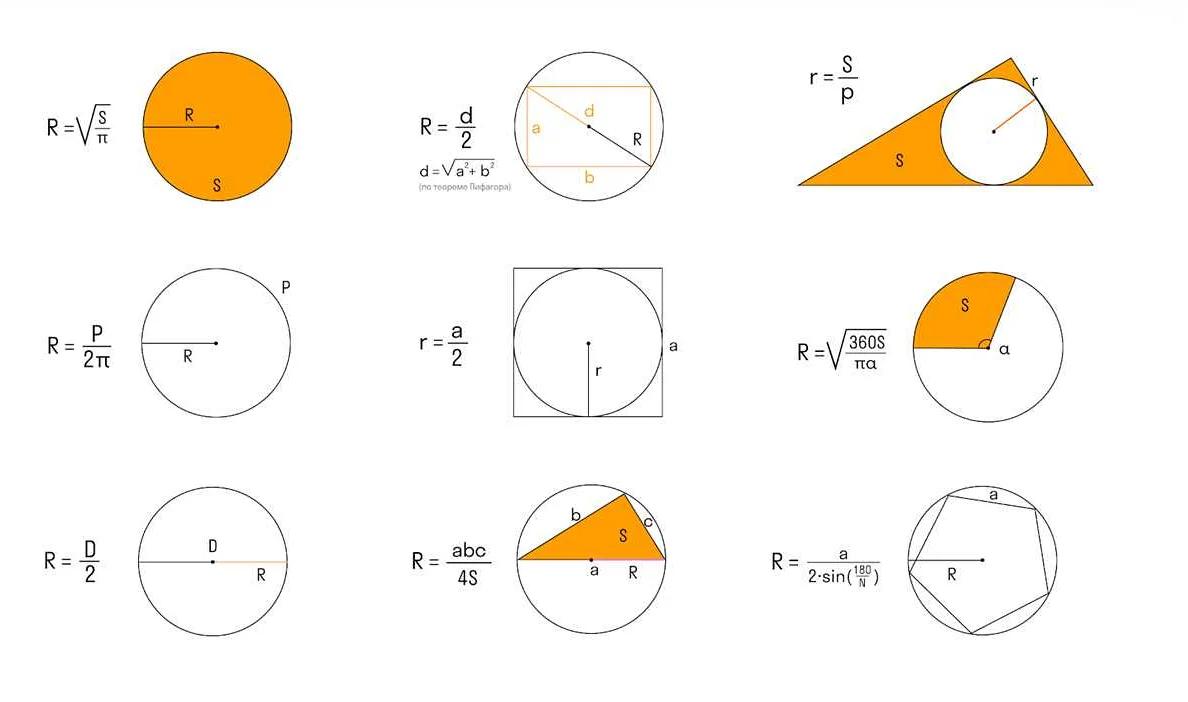
Радиус сферы можно рассмотреть как линию, соединяющую центр сферы с любой из ее точек. Он служит основой для определения других характеристик сферы, таких как диаметр, окружность и площадь поверхности.

Сфера – это трехмерная геометрическая фигура, состоящая из всех точек, находящихся на одинаковом расстоянии от ее центра. Радиус сферы определяет размер и форму сферы. Поверхность сферы представляет собой идеально гладкую и симметричную кривизну.

Примеры использования радиуса и сферы в математике включают расчет объема и площади поверхности сферы, а также решение задач физики и геометрии, связанных с сферическими объектами.

Радиус и вектор

Радиус — это отрезок, который соединяет центр окружности или шара с любой точкой на его границе. Радиус обозначается буквой «r» и используется для измерения длины окружности или поверхности шара. Например, если радиус окружности равен 5 сантиметров, то ее длина будет равна 2 * π * 5 = 10π сантиметров.

Вектор — это направленный отрезок, который характеризуется длиной и направлением. Вектор обозначается буквой со стрелкой над ней, например, вектор «v». Он может быть представлен как геометрически (с помощью стрелки, указывающей направление) или алгебраически (с помощью координат или компонентов). Векторы используются для описания сил, скоростей, перемещений и других физических величин.

Связь между радиусом и вектором в геометрии заключается в том, что радиус окружности или шара может быть представлен вектором, начинающимся в центре и кончающимся на границе фигуры. Это позволяет использовать алгебраические операции с векторами для решения геометрических задач.

Например, если нужно найти точку на окружности, удаленную от центра на определенное расстояние, можно использовать радиус как вектор и переместить его на нужную длину и в нужном направлении.

ПонятиеРадиусВектор

Определение	Отрезок, соединяющий центр окружности или шара с точкой на его границе	Направленный отрезок, характеризующийся длиной и направлением
Обозначение	r	v
Использование	Измерение длины окружности или поверхности шара	Описание сил, скоростей, перемещений и других физических величин

Примеры использования радиуса

Примеры использования радиуса в математике:

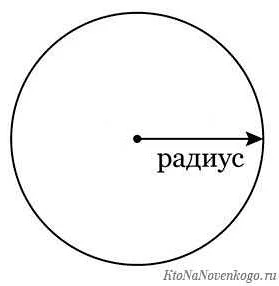
1. В геометрии: радиус является одной из ключевых характеристик окружности. Он определяется как расстояние от центра окружности до ее любой точки на окружности. Радиус используется для вычисления площади и длины окружности, а также для определения положения точки относительно окружности.
2. В физике: радиус может использоваться для описания физических объектов, имеющих форму окружности или сферы. Например, радиус вращения определяет расстояние от оси вращения до каждой точки объекта. Радиус также может использоваться для вычисления объема и площади поверхности шара или сферы.
3. В геодезии: радиус Земли является важным параметром для определения расстояний на поверхности Земли. Радиус Земли используется при измерении длин дуг меридианов и широт.
4. В программировании: радиус может использоваться для работы с графическими объектами, такими как круги, шары, окружности. Расчеты, основанные на радиусе, могут потребоваться для создания графических эффектов, определения коллизий объектов или ограничения их движения.
5. В медицине: радиус используется для измерения длины костей и других анатомических структур. Например, в радиологии радиус представляет собой одну из костей предплечья и может быть измерен для определения длины или углов внутренних структур.

Вопрос-ответ:

Что такое радиус в математике?

Радиус — это расстояние от центра круга или сферы до любой точки на его поверхности.

Как определить радиус круга?

Чтобы определить радиус круга, нужно измерить расстояние от его центра до любой точки на его окружности.

Как использовать радиус в геометрии?

Радиус используется для вычисления площади и длины окружности круга, а также для определения центра и других характеристик фигур.

Какая формула используется для вычисления радиуса круга?

Формула для вычисления радиуса круга имеет вид: r = d/2, где r — радиус, d — диаметр.

Какие еще примеры использования радиуса в математике?

Радиус используется для нахождения объема и площади шара, а также для определения радиус-вектора в векторной алгебре.

Что такое радиус в математике?

Радиус в математике — это линия, которая соединяет центр окружности с любой точкой на ней. Он определяет расстояние от центра окружности до ее границы и является одним из основных понятий геометрии.

Как определить радиус окружности?

Радиус окружности можно определить, зная длину отрезка, соединяющего центр окружности с ее границей. Другой способ — разделить длину окружности на 2*π (2 пи) — это и будет радиус. Также радиус можно выразить через площадь окружности, используя формулу: радиус = √(площадь / π).

Видео по теме: