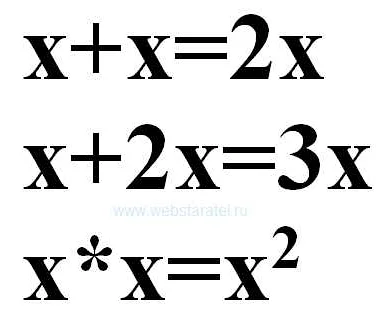Что называют равенством в математике

Равенство в математике — это концепция, согласно которой два объекта или выражения являются эквивалентными или одинаковыми. Равенство играет важную роль в математических уравнениях и формулах, а также в логических рассуждениях и доказательствах. Узнайте больше о понятии равенства в математике и его применении.

Равенство является одним из основных понятий в математике. Оно описывает отношение между двумя математическими объектами, которые имеют одинаковую величину или значение. Равенство выражается с помощью знака «=» и означает, что две стороны данного уравнения равны между собой.

Равенство используется не только в арифметике, но и в других разделах математики, таких как алгебра, геометрия и теория вероятностей. Оно является основой для решения уравнений, построения графиков и доказательства математических теорем.

Примеры равенств:

2 + 2 = 4

x^2 + y^2 = r^2

a + b + c = d

В примерах выше знак «=» означает, что две стороны уравнения имеют одинаковую величину. Например, в уравнении «2 + 2 = 4» обе стороны равны 4. А в уравнении «x^2 + y^2 = r^2» равенство означает, что сумма квадратов переменных x и y равна квадрату радиуса r.

Что такое равенство в математике?

В математике понятие равенства играет важную роль. Равенство означает, что два выражения или объекта имеют одно и то же значение или свойство. В математических уравнениях равенство используется для выражения отношения между двумя сторонами уравнения.

В математике равенство обозначается знаком «=». Например, выражение «2 + 3 = 5» означает, что сумма чисел 2 и 3 равна числу 5. В этом случае «2 + 3» и «5» — это два различных выражения, но они имеют одно и то же значение.

Равенство может быть использовано для сравнения различных объектов или выражений. Например, можно сравнить два числа и установить, равны они друг другу или нет. Если два числа равны, то можно сказать, что они эквивалентны или идентичны друг другу.

В математике равенство может быть использовано для решения уравнений и нахождения неизвестных значений. Уравнение состоит из двух выражений, разделенных знаком равенства. Задача состоит в том, чтобы найти значение неизвестной в уравнении.

Например, уравнение «3x — 4 = 8» означает, что выражение «3x — 4» равно числу 8. Задача состоит в том, чтобы найти значение неизвестной «x», которое удовлетворяет данному уравнению.

Таким образом, равенство в математике является основным понятием, которое позволяет сравнивать и выражать отношения между объектами, выражениями и значениями.

Определение равенства

Равенство может быть использовано для сравнения чисел, переменных, алгебраических выражений, уравнений и т. д.

Равенство имеет несколько свойств:

• Симметричность: если a=b, то b=a.
• Транзитивность: если a=b и b=c, то a=c.
• Рефлексивность: любое выражение равно самому себе.
• Замена: если a=b, то a можно заменить на b и наоборот.

Примеры равенств:

• 2+3=5
• x+2=8
• 2x+3y=5x-2y
• x^2-4=0

Математическая запись равенства

В математике равенство обозначается специальным символом «=». Он используется для указания того, что два выражения или значения равны друг другу. Математическое равенство может представлять собой простое равенство двух чисел, или сложное равенство между выражениями, содержащими переменные и операторы.

Примеры простого равенства:

2 + 2 = 4

5 * 3 = 15

12 — 7 = 5

Примеры сложного равенства:

x + 3 = 8

2y — 4 = 10

3a^2 + 2a — 1 = 0

В этих примерах переменные (x, y, a) принимают определенные значения, при которых равенство выполняется. Чтобы найти значения переменных, удовлетворяющие равенству, используются методы решения уравнений.

Математическая запись равенства позволяет формулировать и решать различные задачи в математике, физике, химии и других науках. Она является одним из основных инструментов математического анализа и моделирования различных процессов.

Примеры равенств

• Пример 2:3 * 5 = 15

  — это пример равенства, где произведение чисел 3 и 5 равно числу 15.

• Пример 3:x + 1 = 7

  — это пример равенства, где неизвестное число x прибавленное к числу 1 равно числу 7.

• Пример 4:5 — y = 2

  — это пример равенства, где разность числа 5 и неизвестного числа y равна числу 2.

Равенство и операции

Равенство может быть использовано с различными операциями, такими как сложение, вычитание, умножение и деление. Например:

• Сложение: 2 + 3 = 5
• Вычитание: 7 — 4 = 3
• Умножение: 2 * 4 = 8
• Деление: 10 / 2 = 5

В этих примерах равенство подтверждает, что результат операции слева от знака «=» равен результату операции справа.

Также равенство может быть использовано с другими математическими операциями, такими как возведение в степень и извлечение корня.

Равенство — это фундаментальное понятие в математике, и оно широко применяется в различных областях, включая алгебру, геометрию, теорию вероятностей и другие.

Равенство и уравнения

Уравнение – это математическое выражение, включающее переменные и знак равенства. Решение уравнения – это значение переменной, при котором уравнение выполняется.

Уравнения могут быть различных типов, например:

• Линейное уравнение: ax + b = c, где a, b, c – коэффициенты, x – переменная.
• Квадратное уравнение: ax^2 + bx + c = 0, где a, b, c – коэффициенты, x – переменная.
• Тригонометрическое уравнение: sin(x) + cos(x) = 1, где x – переменная.

Решение уравнений может быть найдено разными методами, включая графический, аналитический и численный.

Равенство и уравнения играют важную роль в математике и находят применение в различных областях науки, техники и экономики.

Видео по теме:

Вопрос-ответ:

Что такое равенство в математике?

Равенство в математике — это утверждение о равенстве двух выражений или чисел. Если два выражения или числа равны, то они представляют одинаковые значения или имеют одинаковую величину.

Какие примеры можно привести для равенства в математике?

Примеры равенства в математике могут быть разнообразными. Например, 2 + 2 = 4, что означает, что сумма двух чисел 2 равна 4. Еще один пример: 5 * 3 = 15, что означает, что произведение чисел 5 и 3 равно 15.

Как проверить равенство двух выражений?

Для проверки равенства двух выражений необходимо сравнить их значения. Если значения двух выражений совпадают, то выражения равны. Например, чтобы проверить равенство 3 + 4 и 7, нужно сложить 3 и 4, получив 7. Таким образом, выражения равны.

Может ли быть равенство между двумя разными выражениями?

Да, равенство может быть между двумя разными выражениями, если они представляют одинаковые значения. Например, 2 + 3 и 5 — 1 — это два разных выражения, но они оба равны 4, поскольку оба выражения представляют собой сумму двух чисел, дающую 4.

Что означает символ «=» в математике?

Символ «=» в математике обозначает равенство. Когда два выражения или числа связаны символом «=», это означает, что они равны друг другу и представляют одинаковое значение или величину.

Равенство и неравенство

Равенство ( = ) означает, что два выражения или числа имеют одинаковое значение. Например, 2 + 3 = 5 говорит нам, что сумма чисел 2 и 3 равна 5.

Неравенство ( >, ) указывает на то, что одно выражение или число больше, меньше или равно другому. Например, 7 > 5 говорит нам, что число 7 больше числа 5. А выражение 3 + 2 ≤ 6 показывает, что сумма чисел 3 и 2 меньше или равна 6.

Равенство и неравенство могут использоваться в различных математических операциях и уравнениях. Например, в выражении 2x + 3 = 7 равенство указывает на то, что значение выражения 2x + 3 равно 7. А в неравенстве 2x + 3 ≥ 7 неравенство указывает на то, что значение выражения 2x + 3 больше или равно 7.

Таким образом, равенство и неравенство играют важную роль в математике, позволяя нам сравнивать числа и выражения и решать различные математические задачи.

Равенство и эквивалентность

Равенство обозначается знаком «=», который ставится между двумя выражениями или величинами, которые сравниваются. Например, 2 + 3 = 5. В этом примере левая и правая части равны, то есть имеют одинаковое значение.

Важно отличать понятие равенства от понятия эквивалентности. Если два математических выражения имеют разные формы, но при этом имеют одно и то же значение, то они называются эквивалентными. Например, выражения 2 * 3 и 6 являются эквивалентными, так как оба имеют значение 6.

Для обозначения эквивалентности используется специальный символ «≡». Например, 2 * 3 ≡ 6.

Эквивалентность является более широким понятием, чем равенство. Два выражения могут быть эквивалентными, но не равными. Например, x + 1 и x — (-1) являются эквивалентными выражениями, но они не равны, так как имеют разные формы.