Разъяснение понятия равных отношений в математике с использованием калькулятора
Содержимое
- 1 Разъяснение понятия равных отношений в математике с использованием калькулятора
- 1.1 Равные отношения в математике калькулятор
- 1.2 Что такое равные отношения
- 1.3 Основные принципы равных отношений
- 1.4 Понятие равенства в математике
- 1.5 Операции с равными отношениями
- 1.6 Равные отношения и калькулятор
- 1.7 Использование равных отношений в математических вычислениях
- 1.8 Примеры задач с равными отношениями
- 1.9 Вопрос-ответ:
- 1.10 Видео по теме:
Равные отношения в математике означают сравнение двух значений на равенство или неравенство. Используйте наш калькулятор равных отношений для быстрого определения, являются ли два числа равными или неравными.
В математике равенство является одним из основных понятий. Оно подразумевает, что два или более объекта имеют одинаковые значения или свойства. Однако в некоторых случаях необходимо выяснить не только равенство объектов, но и их отношение. Для этого используют понятие равного отношения.
Равное отношение — это особая связь между двумя объектами, которая означает, что эти объекты имеют одинаковые значения или свойства. В математике равное отношение обозначается знаком «=». Например, если имеется выражение «2 + 3 = 5», то оно означает, что сумма чисел 2 и 3 равна числу 5.
Равное отношение является фундаментальным понятием в математике, так как оно используется для формулирования и решения различных задач. На основе равного отношения можно строить уравнения и неравенства, а также проводить различные операции с числами и другими объектами.
Важно отметить, что равное отношение может быть применено не только к числам, но и к другим объектам, таким как переменные, выражения, функции и т.д. Оно позволяет сравнивать и классифицировать объекты на основе их равенства или неравенства.
Равные отношения в математике калькулятор
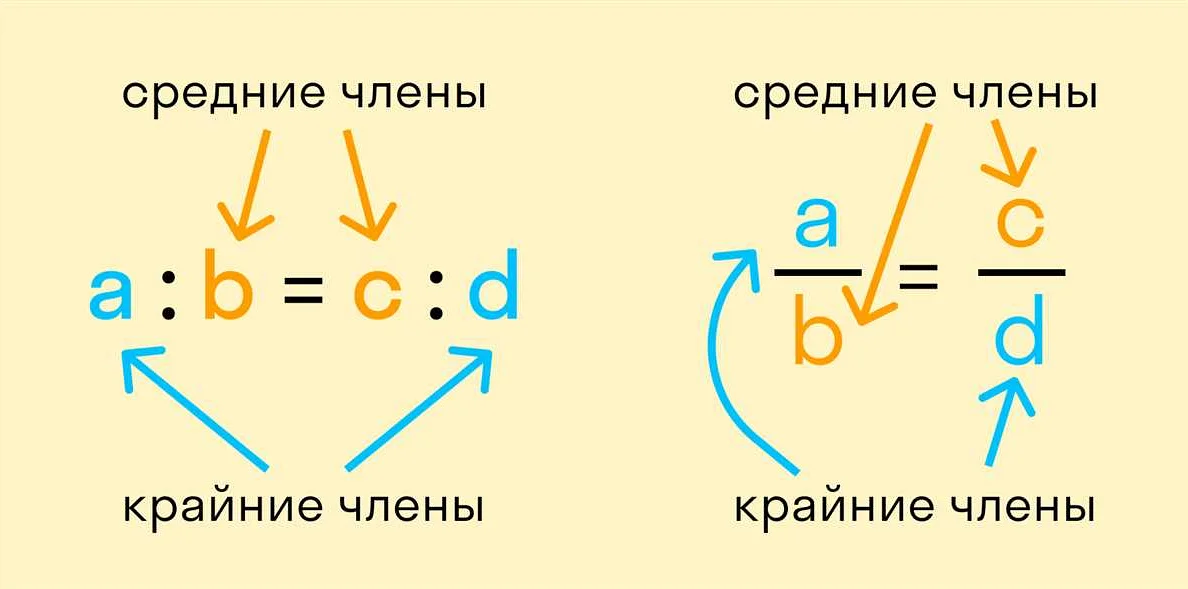
Для определения равных отношений в математике калькулятор использует специальные знаки:
- Знак равенства (=) используется для сравнения двух выражений или чисел. Если выражения или числа имеют одинаковую величину, то они считаются равными.
- Знак неравенства (!=) используется для сравнения двух выражений или чисел. Если выражения или числа имеют различную величину, то они считаются неравными.
Равные отношения в математике калькулятор используются для решения различных задач. Например, равенство может использоваться для определения корней уравнений или проверки правильности математических операций. С помощью неравенства можно сравнивать значения и находить наибольшее или наименьшее число.
Калькулятор позволяет легко и быстро определить, являются ли два выражения или числа равными или неравными. Для этого необходимо ввести значения и знак равенства или неравенства, после чего калькулятор выполнит сравнение и выдаст результат.
Что такое равные отношения
В математике равные отношения играют важную роль при сравнении двух или более величин. Равные отношения возникают, когда две величины или выражения имеют одинаковое значение или равны друг другу.
Равные отношения обозначаются знаком «=». Когда два выражения или величины стоят по обе стороны от знака «=», это означает, что они равны друг другу.
Например, выражения «2 + 3» и «5» равны друг другу, так как оба выражения дают результат 5. Можно записать это следующим образом: 2 + 3 = 5.
Равные отношения могут быть использованы для решения уравнений. Уравнение – это математическое выражение, содержащее знак равенства и неизвестную величину. Решение уравнения – нахождение значения неизвестной величины, при котором обе части уравнения становятся равными.
Например, уравнение «2x + 3 = 7» имеет решение x = 2, так как при подстановке значения 2 вместо x обе части уравнения становятся равными: 2 * 2 + 3 = 7.
Равные отношения также используются для сравнения величин. Если две величины равны друг другу, это означает, что они имеют одинаковую величину или количество. Например, если у вас есть 3 яблока и 3 апельсина, то можно сказать, что количество яблок равно количеству апельсинов.
В математике равные отношения важны для установления равенства между выражениями, решения уравнений и сравнения величин. Знание равных отношений позволяет более точно работать с математическими операциями и анализировать различные математические модели.
Основные принципы равных отношений
Равные отношения в математике играют важную роль и имеют свои основные принципы. Они позволяют сравнивать и устанавливать равенство между различными элементами или выражениями.
Вот некоторые основные принципы равных отношений:
1. Равное с равным равно: если два элемента или выражения полностью идентичны, то они равны между собой. Например, 2 + 3 = 5.
2. Равенство можно сохранить при выполнении одинаковых операций с обеими сторонами равенства. Например, если у нас есть уравнение 2x — 3 = 7, то мы можем прибавить 3 к обеим сторонам и получить 2x = 10.
3. Равным множествам соответствуют равные числа. Если два множества содержат одинаковые элементы, то они равны между собой. Например, {1, 2, 3} = {3, 2, 1}.
4. Равные отношения могут быть использованы для решения уравнений. Если два выражения равны между собой, то мы можем использовать это равенство для нахождения значения переменной. Например, если у нас есть уравнение 2x + 5 = 15, то мы можем выразить значение x, поделив обе стороны на 2 и получив x = 5.
Это лишь некоторые из основных принципов равных отношений в математике. Понимание и применение этих принципов помогает в решении уравнений и сравнении различных элементов и выражений.
Понятие равенства в математике
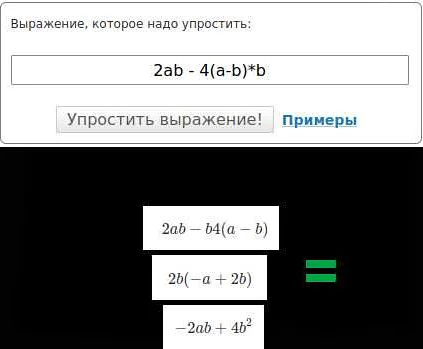
Равенство в математике используется для сравнения чисел и алгебраических выражений. Например, уравнение x + 5 = 10 означает, что значение переменной x равно 5, так как при подстановке значения 5 вместо x получаем верное равенство 5 + 5 = 10.
Равенство имеет свойства, которые могут использоваться для решения уравнений и доказательства математических утверждений. Одно из таких свойств равенства – свойство замены. Согласно этому свойству, если в равенстве заменить одинаковые выражения на одно и то же выражение, получится верное равенство. Например, из уравнения x + 3 = 7 можно получить равенство 2 + 3 = 7, заменив переменную x на число 2.
В математике равное необходимо отличать от подобного или эквивалентного. Подобные выражения имеют одинаковую структуру, но значения могут быть разными. Например, выражения 2x + 3 и 3 + 2x являются подобными, так как имеют одинаковую структуру и можно получить одно из другого простой перестановкой слагаемых.
Знание понятия равенства в математике является основой для решения уравнений, алгебраических задач и доказательств математических теорем и свойств.
Операции с равными отношениями

Операции с равными отношениями включают:
ОперацияОписаниеПример
| Сложение | Складывает два равных значения или выражения | 2 + 2 = 4 |
| Вычитание | Вычитает одно равное значение или выражение из другого | 5 — 3 = 2 |
| Умножение | Умножает два равных значения или выражения | 3 * 3 = 9 |
| Деление | Делит одно равное значение или выражение на другое | 10 / 2 = 5 |
Также можно применять операции сравнения, такие как:
ОперацияОписаниеПример
| Больше | Проверяет, является ли одно значение больше другого | 5 > 3 |
| Меньше | Проверяет, является ли одно значение меньше другого | 2 < 4 |
| Равно | Проверяет, являются ли два значения или выражения равными | 4 = 4 |
| Больше или равно | Проверяет, является ли одно значение больше или равным другому | 7 >= 5 |
| Меньше или равно | Проверяет, является ли одно значение меньше или равным другому | 3 |
Операции с равными отношениями позволяют устанавливать связи и сравнивать значения в математических выражениях, что является важным инструментом в решении различных задач и уравнений.
Равные отношения и калькулятор

Калькулятор — это инструмент, который позволяет выполнять различные математические операции, включая проверку равенства выражений. С помощью калькулятора можно удобно сравнивать числа и проверять, являются ли они равными.
Для проверки равенства двух чисел с помощью калькулятора необходимо ввести оба числа и выбрать операцию равенства. Если результат равенства равен «true», это означает, что числа равны. Если результат равенства равен «false», это означает, что числа не равны.
Калькулятор также может использоваться для проверки равенства более сложных выражений, включая уравнения и неравенства. Для этого необходимо ввести выражение в калькулятор и выбрать операцию равенства. Если результат равенства равен «true», это означает, что выражения равны. Если результат равенства равен «false», это означает, что выражения не равны.
ПримерОписаниеРезультат
| 2 + 2 = 4 | Проверка равенства двух чисел | true |
| 3 * 5 = 15 | Проверка равенства двух чисел | true |
| 4 + 3 = 7 | Проверка равенства двух чисел | true |
| 2 + 2 = 5 | Проверка равенства двух чисел | false |
| 3 * 5 = 18 | Проверка равенства двух чисел | false |
Использование калькулятора для проверки равенства выражений помогает убедиться в правильности математических выкладок и сделать вывод о равенстве или неравенстве чисел и выражений.
Использование равных отношений в математических вычислениях
В математических вычислениях равенство используется для решения уравнений, составления систем уравнений и выполнения различных операций. Чтобы показать равенство между двумя выражениями, используется знак «=». Например, выражение «2 + 3 = 5» означает, что сумма чисел 2 и 3 равна 5.
Равенство также может быть использовано для сравнения объектов или выражений на равенство или неравенство. Например, выражение «5 > 3» означает, что число 5 больше числа 3. Также можно использовать символы «≠» (не равно), «» (больше), «≤» (меньше или равно) и «≥» (больше или равно) для указания неравенств между выражениями.
Равные отношения используются в различных областях математики, таких как алгебра, геометрия, теория вероятностей и других. Они позволяют проводить точные и строгие математические рассуждения и доказательства.
Важно уметь правильно использовать равные отношения в математических вычислениях, чтобы получать верные результаты и решения задач. Также следует помнить, что равные отношения могут быть использованы для установления связи между различными математическими концепциями и теориями.
Примеры задач с равными отношениями
- Пример 1: В коробке лежит 12 красных шаров и 8 синих шаров. Найдите отношение количества красных шаров к синим шарам.
- Пример 2: В классе 20 мальчиков и 15 девочек. Каково отношение количества мальчиков к девочкам?
- Пример 3: В банке имеется 4 монеты достоинством в 10 рублей и 6 монет достоинством в 5 рублей. Какое отношение существует между количеством монет достоинством в 10 рублей и 5 рублей?
- Пример 4: В одном ящике 30 яблок и 50 апельсинов. Какое отношение количества яблок к апельсинам?
- Пример 5: В книжной полке 24 книги по истории и 16 книг по математике. Какой тип отношения между количеством книг по истории и математике?
Вопрос-ответ:
Что такое равные отношения в математике?
Равные отношения в математике — это отношения, которые устанавливаются между двумя или более объектами, когда они имеют одинаковую величину или значение.
Как определить равные отношения с помощью калькулятора?
С помощью калькулятора можно определить равные отношения, сравнивая числа или выражения и проверяя, равны они или нет. Для этого нужно ввести числа в калькулятор и сравнить результаты. Если результаты равны, то отношения также равны.
Зачем нужны равные отношения в математике?
Равные отношения в математике используются для сравнения объектов, выражений или значений. Они помогают устанавливать равенство между различными объектами и выполнять разнообразные математические операции.
Какие свойства имеют равные отношения?
Равные отношения обладают следующими свойствами: 1) Рефлексивность — любой объект равен самому себе; 2) Симметричность — если один объект равен другому, то и другой объект равен первому; 3) Транзитивность — если первый объект равен второму, а второй объект равен третьему, то первый объект также равен третьему.
Какие операции можно выполнять с равными отношениями в математике?
С равными отношениями в математике можно выполнять разнообразные операции, такие как сложение, вычитание, умножение и деление. При выполнении этих операций равные отношения сохраняются, то есть если два объекта равны, то и результат операции с ними будет также равен.
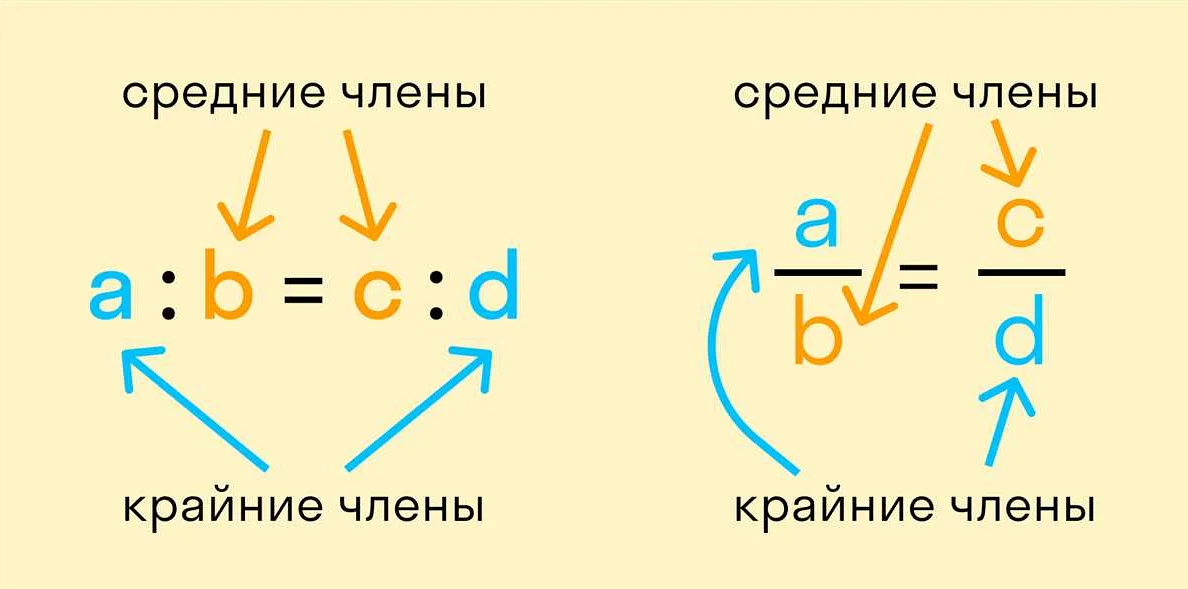

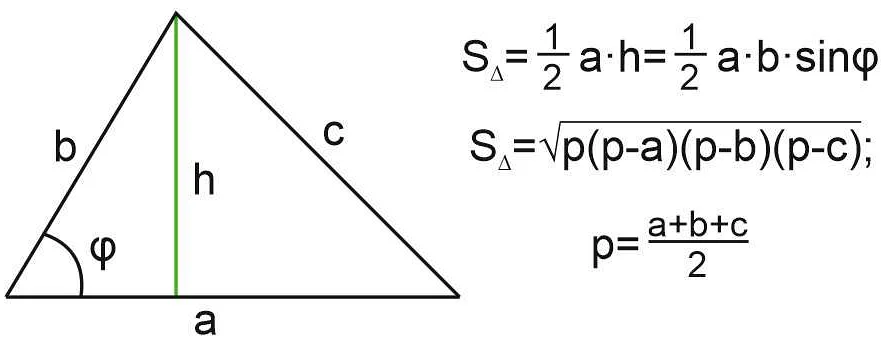

Равные отношения в математике калькулятор — это основной принцип, который помогает нам сравнивать и оценивать числа с помощью математических операций. Этот принцип позволяет нам определить, являются ли два числа равными или разными, и какие из них больше или меньше. Например, если на калькуляторе мы вводим 2+2 и получаем результат 4, то мы можем сказать, что эти два числа равны друг другу. Если же мы вводим 3 и 5 и получаем результат 8, то мы можем сказать, что 3 меньше 5. Равные отношения помогают нам легко и точно работать с числами, делая математику более понятной и доступной для каждого.
Равные отношения в математике калькулятор это основа для понимания и решения различных задач. Этот инструмент позволяет сравнивать значения и определять, являются ли они равными или нет. Он широко используется в школьном и профессиональном обучении. Калькулятор помогает нам понять и применить концепцию равных отношений в различных областях, таких как алгебра, геометрия, физика и экономика. Он облегчает выполнение сложных вычислений и упрощает нахождение правильных ответов. Одним из простых примеров равных отношений является сравнение двух чисел. Если два числа имеют одинаковое значение, то мы можем сказать, что они равны. Например, 5 + 3 = 8, а 4 + 4 = 8. Оба этих выражения демонстрируют равные отношения, где сумма обоих равна 8. Калькулятор также помогает нам решать уравнения и неравенства. Он может определить, равны ли два выражения или нет. Это особенно полезно при решении сложных математических проблем, где необходимо сравнивать и анализировать большое количество данных. В целом, равные отношения в математике калькулятор — это мощный инструмент, который помогает нам лучше понять и применять математические концепции. Он способствует более точным и эффективным вычислениям, что является необходимым навыком в современном мире.