Что такое sec x в математике

sec x в математике представляет собой секанс функции x, которая является обратной функцией косеканса. Секанс определяется как обратная косинусу, и обозначается как sec x. Он представляет отношение гипотенузы прямоугольного треугольника к его прилежащему катету. Sec x также может быть выражен как 1/cos x, где cos x — косинус функции x. Sec x обладает рядом свойств и используется в различных областях математики и физики.

sec x — это функция, которая является обратной косинусу. Она обозначает секанс угла x и является одной из шести тригонометрических функций, используемых в математике.

Функция sec x выражает отношение гипотенузы и прилежащего катета прямоугольного треугольника. Формула для вычисления sec x выглядит следующим образом: sec x = 1/cos x. Таким образом, sec x равно обратному значению косинуса угла x.

Свойства функции sec x можно вывести из свойств косинуса. Например, sec x имеет период равный 2π и асимптоты в точках π/2 + nπ и -π/2 + nπ, где n — любое целое число. Кроме того, sec x является нечетной функцией, то есть sec(-x) = -sec x.

Функция sec x широко применяется в физике, инженерии и других областях, где важно вычисление углов и применение тригонометрии. Она является одной из основных функций, которые помогают нам понять и изучать свойства и закономерности углов и треугольников.

Определение секанса в математике

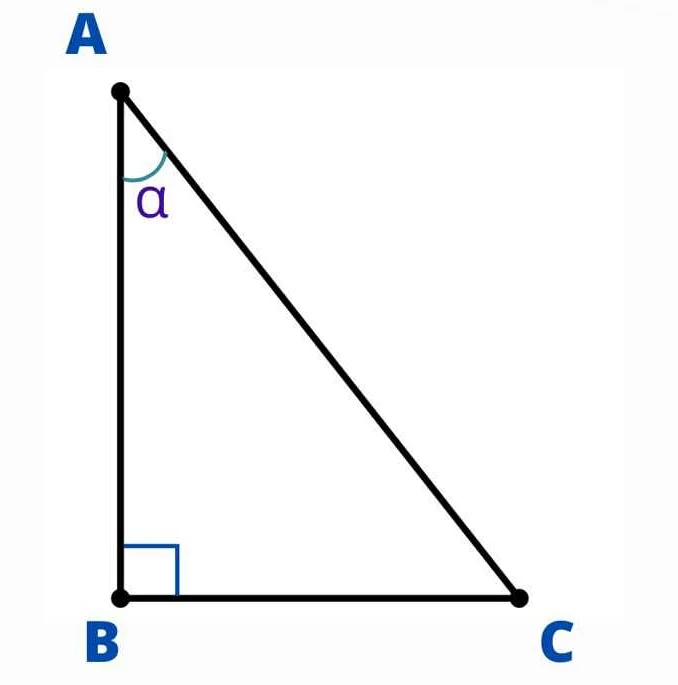
Для любого угла x в радианах секанс(x) равен отношению гипотенузы прямоугольного треугольника к его стороне, прилегающей к углу x. Математически секанс(x) выражается следующей формулой:

sec(x) = 1 / cos(x)

Секанс функционирует на всем множестве действительных чисел, кроме точек, где косинус равен нулю. В этих точках секанс не определен.

Секанс имеет несколько основных свойств, таких как периодичность, нечетность и ограниченность. Знание этих свойств помогает в решении уравнений и построении графиков секанса.

Свойства секанса

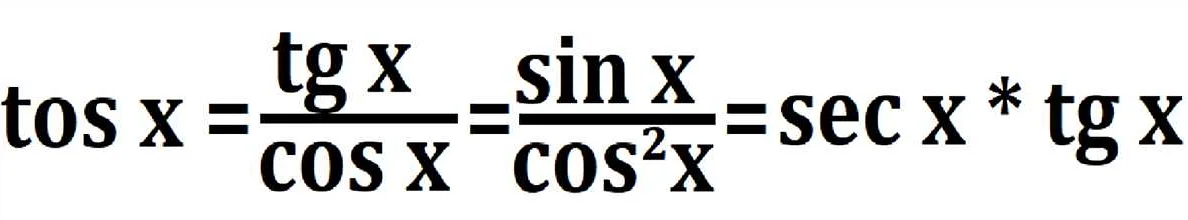
Секанс x может быть выражен через косеканс x как:

ФункцияВыражение

Секанс x	sec x = 1 / cos x
Косеканс x	csc x = 1 / sin x

Секанс имеет несколько свойств, которые могут быть использованы при решении математических задач:

1. Периодичность: секанс является периодической функцией с периодом π.
2. Знак: секанс положителен на интервалах, где косинус положителен, и отрицателен на интервалах, где косинус отрицателен.
3. Значения: секанс принимает любые действительные значения, кроме нуля, в котором он не определен.
4. Симметрия: секанс является нечетной функцией, то есть sec (-x) = -sec x.
5. Соотношение: sec x = 1 / cos x, что позволяет выразить секанс через косинус.

Эти свойства секанса могут быть использованы при работе с тригонометрическими уравнениями, графиками функций и другими математическими задачами, где требуется использование секанса.

График секанса

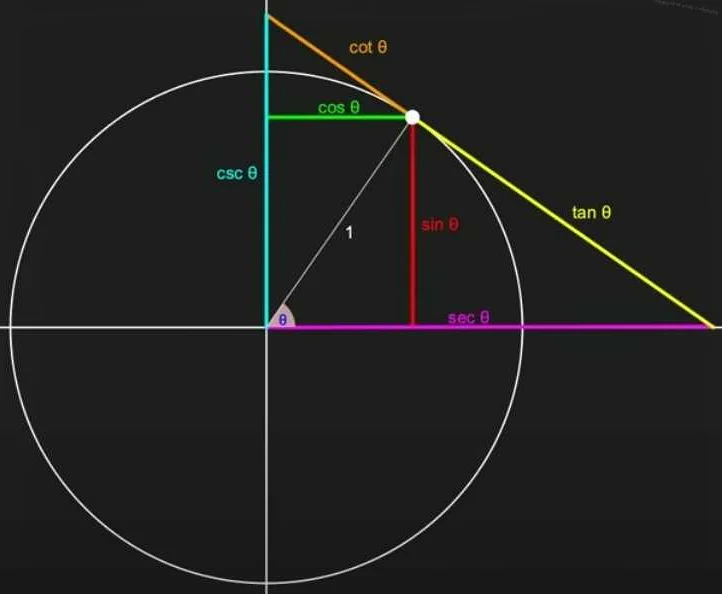
• Функция секанса имеет период равный периоду функции косеканса и асимптоты в точках, где косеканс равен нулю.
• График функции секанса отличается от графика функции косеканса только тем, что пересекает ось ординат в точке 1, а не в бесконечности.
• График секанса симметричен относительно оси абсцисс.

График секанса можно построить, рассчитав значения функции для различных значений аргумента и соединив полученные точки прямыми линиями. С помощью графика секанса можно анализировать значения функции на различных участках и изучать ее основные свойства.

Основные формулы секанса

1. Определение:

Секанс функции x обозначается как sec x и определяется как обратная функция косекансу:

sec x = 1 / cos x

2. Отношение к другим тригонометрическим функциям:

Секанс можно выразить через синус и косинус:

sec x = 1 / cos x = 1 / (1 / csc x) = csc x / 1 = csc x

3. Соотношение синуса, косинуса и тангенса:

Используя определение секанса, можно получить следующее соотношение синуса, косинуса и тангенса:

sin x = 1 / csc x

cos x = 1 / sec x

tan x = sin x / cos x = (1 / csc x) / (1 / sec x) = sec x / csc x = sec x

Это были некоторые основные формулы, связанные с секансом. Они могут быть полезны при решении задач и анализе тригонометрических функций.

Секанс в тригонометрических уравнениях

Секанс может быть использован в тригонометрических уравнениях для решения задач, связанных с поиском значений переменной x. В таких уравнениях секанс может совпадать с другими тригонометрическими функциями, а также с числами и переменными.

Для решения тригонометрических уравнений с секансом необходимо использовать алгебраические методы и свойства тригонометрических функций. Одним из подходов может быть приведение уравнения к более простому виду, замена переменных, а также использование тригонометрических тождеств.

Применение секанса в тригонометрических уравнениях позволяет решать различные задачи, связанные с геометрией, физикой и инженерными науками. Например, секанс может быть использован для определения углов наклона, высот, дальностей и других величин.

Применение секанса в геометрии

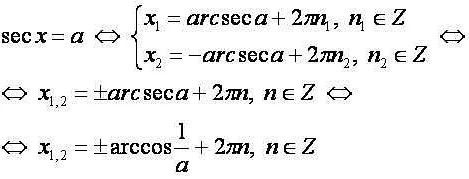
Одно из основных применений секанса в геометрии – нахождение длины отрезка, соединяющего центр окружности с точкой окружности, находящейся на терминальном луче угла. Используя секанс, можно выразить эту длину через радиус окружности и угол, образованный этим отрезком с положительным направлением оси x.

Для нахождения длины отрезка можно воспользоваться формулой:

AB = r * sec(θ),

где AB – длина отрезка, соединяющего центр окружности (точку A) с точкой окружности (точкой B), r – радиус окружности, а θ – угол между положительным направлением оси x и лучом, соединяющим центр окружности с точкой окружности.

Секанс также может быть применен для нахождения углов и расстояний в треугольниках и других геометрических фигурах. Например, при известной длине стороны треугольника и соответствующему углу, можно использовать секанс для нахождения длины прилежащей стороны.

Таким образом, секанс является полезной функцией в геометрии, позволяющей решать различные задачи и находить геометрические параметры в различных фигурах.

Секанс и другие тригонометрические функции

Тригонометрические функции — это функции, которые связывают углы и стороны треугольников. Кроме секанса, к основным тригонометрическим функциям относятся синус (sin), косинус (cos), тангенс (tan), котангенс (cot) и косеканс (cosec).

Синус (sin) определяется как отношение противолежащего катета к гипотенузе треугольника. Косинус (cos) определяется как отношение прилежащего катета к гипотенузе треугольника. Тангенс (tan) определяется как отношение противолежащего катета к прилежащему катету. Котангенс (cot) определяется как обратное значение тангенса, то есть cot(x) = 1/tan(x). Косеканс (cosec) определяется как обратная функция к синусу, то есть cosec(x) = 1/sin(x).

Как и другие тригонометрические функции, секанс имеет ряд свойств и идентичностей, которые могут быть использованы для упрощения выражений и решения уравнений. Он также имеет график, который может быть использован для визуализации его поведения и свойств.

Использование тригонометрических функций, включая секанс, широко распространено в математике, физике, инженерии и других науках. Они играют важную роль в решении задач, связанных с углами, колебаниями и волнами, а также в моделировании и анализе различных явлений.

Вопрос-ответ:

Что такое sec x?

Sec x — это функция, обратная косинусу, которая выражается как 1/cos x. Она определяется как отношение гипотенузы прямоугольного треугольника к его прилежащему катету.

Какая формула определяет sec x?

Формула sec x = 1/cos x определяет значение функции sec x. Она показывает, что sec x является обратной функцией косинуса и равна отношению единицы к значению cos x.

Какие свойства имеет функция sec x?

Функция sec x обладает несколькими свойствами. Одно из них — sec x принимает значения только в интервале (-бесконечность, -1] и [1, +бесконечность). Она также является периодической функцией с периодом 2π. Кроме того, sec x является нечетной функцией, что означает, что sec (-x) = -sec x.

Как можно использовать функцию sec x в математике?

Функция sec x имеет множество применений в математике. Она может использоваться для решения уравнений и неравенств, а также для нахождения значений других тригонометрических функций, таких как cosec x, tan x и cot x. Кроме того, sec x может быть полезна при изучении геометрии и алгебры, так как она помогает определить отношение сторон треугольника и решать задачи, связанные с углами и треугольниками.

Видео по теме: