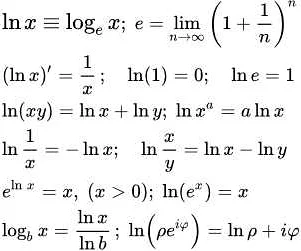Что значит обратная е в математике

Обратная е в математике — это математическая константа, которая обозначается как e^(-1) или 1/e. Она играет важную роль в различных областях математики, физики и экономики, таких как дифференциальное и интегральное исчисление, теория вероятностей и экономические модели.

Обратная е, также известная как число Эйлера или экспонента, является одной из наиболее важных математических констант. Она определяется как предел функции (1 + 1/n)^n при n, стремящемся к бесконечности. Значение обратной е приближенно равно 2.71828.

Обратная е обладает множеством уникальных и интересных свойств. Во-первых, она является иррациональным числом, то есть не может быть представлена в виде дроби. Это делает е его необычным и сложным для вычисления числом.

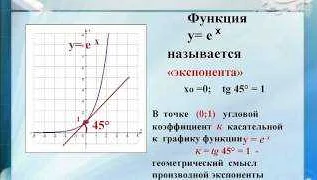
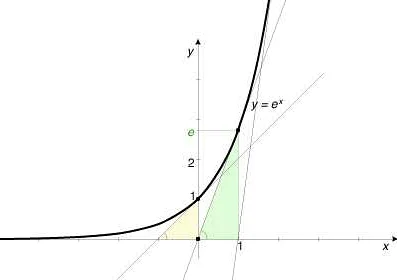
Важнейшее свойство обратной е заключается в том, что она является основанием экспоненциальной функции. Экспоненциальная функция с основанием е обозначается как exp(x) или e^x, где x — любое вещественное число. Такая функция встречается во многих областях математики и естествознания, таких как теория вероятностей, статистика, физика, экономика и другие.

Обратная е имеет также свои применения в финансовой математике, где она используется для вычисления сложных процентных ставок и накопленных процентов. Более того, число Эйлера помогает нам понять различные процессы роста и декремента, а также моделировать системы с экспоненциальным ростом или затуханием. Таким образом, обратная е является неотъемлемым инструментом в решении различных задач, связанных с экспоненциальными функциями и научными исследованиями.

Математика

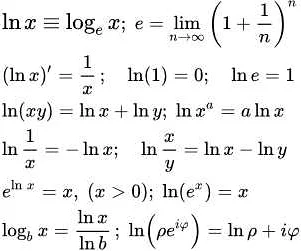
Математика включает в себя множество различных разделов, включая алгебру, геометрию, теорию чисел, математический анализ, теорию вероятностей и дискретную математику. Каждый из этих разделов имеет свои собственные понятия, методы и приложения.

Математика широко используется в научных исследованиях, разработке новых технологий и решении практических задач. Она позволяет моделировать и анализировать сложные системы, прогнозировать результаты экспериментов, оптимизировать процессы и принимать обоснованные решения.

Математика также способствует развитию логического мышления, абстрактного мышления и критического мышления. Она помогает развивать навыки решения проблем, построения доказательств и анализа информации.

В целом, математика играет важную роль в нашей жизни и является неотъемлемой частью современного мира. Она помогает нам понимать и объяснять законы природы, создавать новые технологии и улучшать качество нашей жизни.

Теория чисел

Одним из основных понятий в теории чисел является понятие простого числа. Простые числа являются основными строительными блоками всех целых чисел, так как любое целое число может быть разложено на произведение простых чисел. Также теория чисел изучает свойства простых чисел и различные алгоритмы для их нахождения.

Другим важным понятием в теории чисел является делимость. Делимость определяет, делится ли одно число на другое без остатка. Например, число 6 делится на 2, так как 6 = 2 * 3. Теория чисел изучает различные свойства делимости и различные методы для проверки делимости.

Теория чисел также занимается исследованием сравнений по модулю. Сравнение по модулю определяет равенство или неравенство двух чисел с учетом их остатков при делении на определенное число. Сравнения по модулю часто используются в криптографии и различных алгоритмах шифрования.

Теория чисел имеет множество применений в различных областях, таких как криптография, теория кодирования, алгоритмы и многих других. Она играет важную роль в различных аспектах современной науки и технологий.

Обратная е

Обратная е обладает следующими свойствами:

Свойство	Значение
Обратное число	e * (1/e) = 1
Обратное число для произведения	(a * b) * (1/e) = a * (b * (1/e))
Обратное число для степени	(an) * (1/e) = an * (1/e)

Обратная е находит применение в различных областях математики, физики и техники. Она используется в решении дифференциальных уравнений, в экономике при моделировании процентной ставки, а также в теории вероятности и статистике.

Определение

Обратной единицей числа а называется такое число, при умножении на которое, произведение будет равно единице.

Обратная единица обозначается символом 1/a.

Для любого числа а, отличного от нуля, обратное число всегда существует и единственно.

Свойства обратной единицы:

• Умножение числа на его обратное даёт 1: a * 1/a = 1
• Умножение обратной единицы на число даёт 1: 1/a * a = 1
• Обратная единица для единицы равна единице: 1/1 = 1

Что такое обратная е?

Обратная е обладает множеством уникальных свойств и является основой для многих математических и физических формул. Ее можно представить как бесконечную сумму ряда:

• Обратная е повышает число в степень при изменении единицы времени.
• Обратная е является производной от себя самой.
• Обратная е является пределом (при стремлении n к бесконечности) последовательности (1 + 1/n)^n.

Обратная е широко используется в различных областях науки и инженерии, таких как физика, статистика, финансы и компьютерные науки. Она активно применяется в моделировании экспоненциального роста, распределении вероятностей и решении дифференциальных уравнений.

Свойства

1. Умножение на обратную е даёт единицу: e \cdot \frac{1}{e} = 1.
2. Обратная е является нейтральным элементом для сложения в экспоненциальной форме: e^0 = 1.
3. Производная обратной функции f(x) = \ln(x) равна \frac{1}{x}. То есть, если y = \ln(x), то \frac{{dy}}{{dx}} = \frac{1}{{x}}.
4. Обратная функция f(x) = e^x является своей собственной производной: \frac{{dy}}{{dx}} = e^x.
5. Обратная е используется во многих приложениях, включая финансовую математику, теорию вероятностей, физику и инженерию.

Все эти свойства делают обратную е одним из наиболее важных чисел в математике и дают ей специальное место в различных областях науки и техники.

Свойства обратной е

1. Умножение и деление: Обратная е обладает свойством, что при умножении на нее, любое число сохраняет свое значение. То есть, e^(-1) * x = x для любого числа x. Аналогично, при делении числа на обратную е, значение числа не изменяется.

2. Возведение в степень: При возведении числа в степень обратной е, получается значения, близкие к нулю. Например, e^(-1)^n = 1/e^n, что при n, приближающемся к бесконечности, стремится к нулю.

3. Производная: Обратная е играет важную роль в дифференциальном и интегральном исчислении. Производная функции e^x равна самой функции, то есть d/dx(e^x) = e^x. Это свойство позволяет использовать обратную е для решения различных задач, связанных с изменением функций во времени.

4. Вероятность: Обратная е также используется в вероятностных расчетах. Например, в теореме Чебышева об оценке вероятности отклонения случайной величины от ее математического ожидания, обратная е является важным компонентом формулы.

Все эти свойства делают обратную е неотъемлемой частью математики, физики, экономики и других наук. Она играет важную роль в различных областях и имеет множество приложений и интерпретаций.

Видео по теме:

Вопрос-ответ:

Что такое обратная е в математике?

Обратная е в математике представляет собой обратную функцию к экспоненциальной функции. Она обозначается как ln(x) и определяется как число, возводимое в экспоненту e, чтобы получить x. Например, если ln(x) = y, то e^y = x.

Какие свойства имеет обратная е в математике?

Обратная е обладает несколькими важными свойствами. Во-первых, ln(1) = 0, что является следствием того, что e^0 = 1. Во-вторых, ln(e) = 1, что означает, что e возводим в степень 1, получаем e. Кроме того, обратная функция обладает свойствами логарифмической функции, такими как свойство логарифма произведения и свойство логарифма степени.

Как можно использовать обратную е в математике?

Обратная е имеет широкое применение в различных областях математики и науки. Она используется для решения уравнений, моделирования роста и распада, нахождения процентных ставок, а также в статистике и вероятности. Также она является важной составляющей в определении натурального логарифма и его свойств.

Какие альтернативные обозначения существуют для обратной е?

Обратная функция экспоненты может быть обозначена не только как ln(x), но и как log_e(x) или просто как log(x), если база логарифма не указана. Также существуют другие обозначения для обратной е, используемые в различных областях математики и науки.

Как рассчитать обратную е в математике?

Для рассчета обратной е в математике можно использовать специальные таблицы или калькуляторы, которые имеют встроенную функцию ln(x). Также существуют математические формулы и методы, позволяющие вычислить обратную функцию экспоненты с высокой точностью.

Что такое обратная е в математике?

Обратная е в математике — это число, которое при возведении в степень даёт единицу. Оно обозначается как e^(-1) или 1/e и является основанием натурального логарифма.

Какие свойства у обратной е в математике?

Обратная е в математике обладает несколькими свойствами. Во-первых, e^(-1) удовлетворяет условию e^(x + y) = e^x * e^y, где x и y — произвольные действительные числа. Во-вторых, e^(-x) равно 1/e^x. Кроме того, обратная е является основанием натурального логарифма, то есть ln(e) = 1.

Применение

1. В алгебре и анализе обратная функция используется для решения уравнений. Если у нас есть функция f(x), то обратная функция f-1(x) позволяет нам найти значения x, при которых f(x) равно заданному значению.
2. В геометрии обратная функция может использоваться для определения точек на плоскости, которые находятся на одинаковом расстоянии от данной точки или прямой.
3. В теории вероятности и статистике обратная функция может использоваться для нахождения квантилей распределений. Квантиль определяет значение, ниже которого находится определенная доля выборки.
4. В экономике и финансах обратная функция может применяться для моделирования и анализа сложных систем, таких как рынки или портфели инвестиций.
5. В компьютерной графике и компьютерных играх обратная функция может использоваться для преобразования координат объектов на экране, позволяя управлять их положением и движением.

Обратная функция является мощным математическим инструментом, который применяется во многих областях науки и техники. Понимание ее свойств и применение позволяет решать сложные задачи и получать новые знания о мире вокруг нас.

Где применяется обратная е?

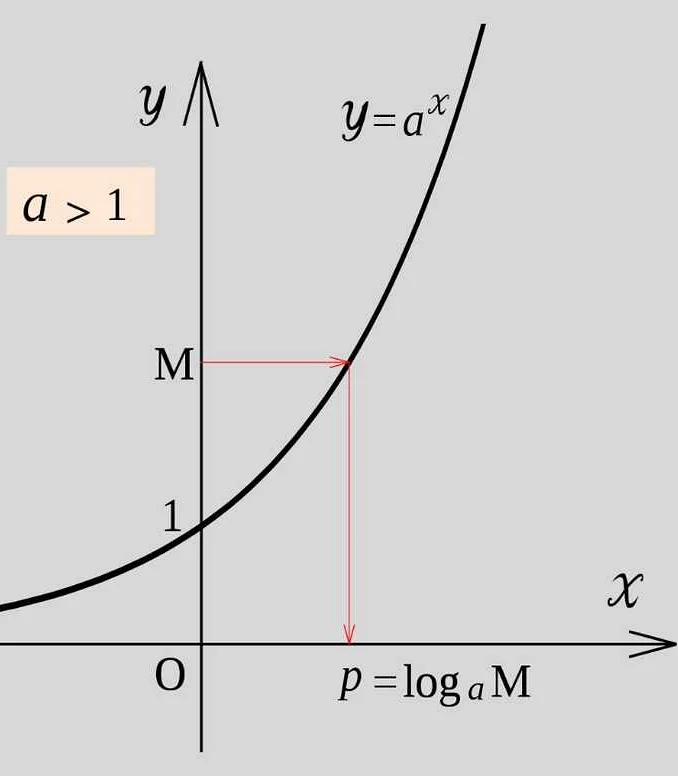
Одним из наиболее известных применений обратной е является математическая анализ, где она используется для определения непрерывной и дифференцируемой функции. Обратная е также играет ключевую роль в теории вероятностей и статистике, где она используется для моделирования случайных процессов и распределений.

В физике обратная е используется для описания множества физических явлений, таких как рост популяции, затухание сигнала и распределение тепла. Она также является основой для ряда физических законов, включая закон Ньютона о кулоновском взаимодействии и закон Ома в электрических цепях.

Обратная е применяется также в экономике и финансах, где она используется для моделирования экономических процессов и расчета ставок дисконтирования. Она также играет важную роль в теории управления и оптимальном управлении.

Кроме того, обратная е находит свое применение в компьютерной науке и информационных технологиях. Она используется для моделирования и анализа алгоритмов, оптимизации программного кода и решения различных задач.

В общем, обратная е является универсальной математической константой, которая находит применение практически во всех областях науки и техники.