Что такое tan в математике

tan в математике — это тригонометрическая функция, которая вычисляет тангенс угла. Зная угол, можно использовать tan для вычисления соответствующего значения тангенса. Эта функция широко применяется в различных областях, включая физику, инженерию и геометрию.

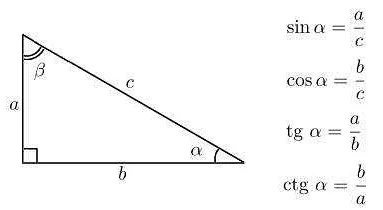
В математике тангенс (tan) является одной из трех основных тригонометрических функций, вместе с синусом (sin) и косинусом (cos). Тангенс угла определяется как отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике. Это позволяет использовать тангенс для решения различных задач, связанных с треугольниками и углами.

Тангенс широко применяется в геометрии, физике, инженерии и других областях. Он может использоваться для нахождения неизвестных углов или сторон треугольника, а также для расчета склонов, углов наклона и других геометрических параметров. Кроме того, тангенс может быть полезен при решении задач, связанных с колебаниями, электричеством и другими дисциплинами.

Знание тангенса и его свойств может быть полезным инструментом для понимания и анализа различных явлений в нашей физической и математической реальности.

Таким образом, тангенс играет важную роль в математике и ее приложениях, обеспечивая нам не только практические инструменты для решения задач, но и глубокое понимание структуры и связей в нашей физической вселенной.

Определение тангенса

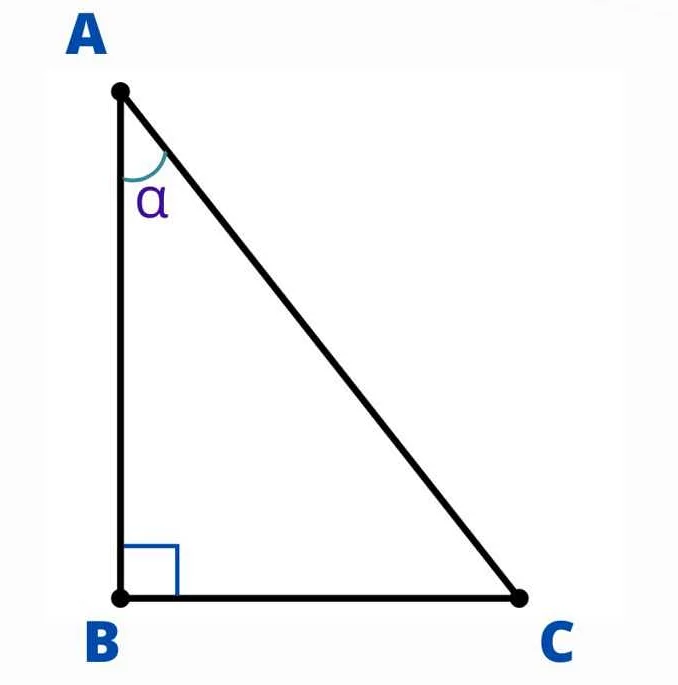
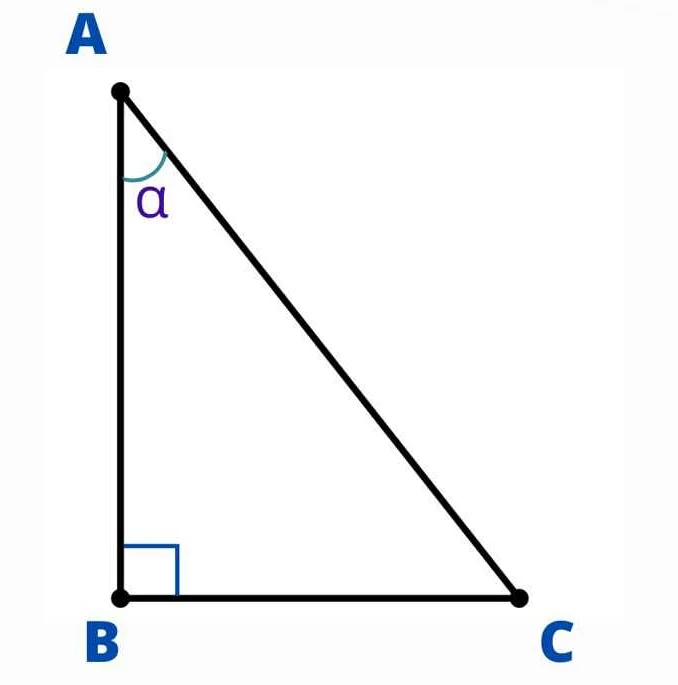
В прямоугольном треугольнике, если угол между горизонтальной осью и стороной треугольника равен θ, то тангенс этого угла (обозначается как tan(θ)) определяется как отношение противолежащего катета к прилежащему катету.

Формула для вычисления тангенса:

tan(θ) = противолежащий катет / прилежащий катет

Значение тангенса может быть положительным или отрицательным, в зависимости от значения угла θ.

Тангенс широко используется в геометрии, физике, инженерии и других науках для решения различных задач, связанных с треугольниками и углами.

Видео по теме:

Тангенс как функция

Тангенс может быть использован для решения различных задач, связанных с геометрией, физикой, инженерией и другими областями науки и техники. Он позволяет вычислять углы и расстояния, а также решать задачи, связанные с траекториями движения, скоростью и ускорением.

Тангенс обладает следующими свойствами:

• Определение: tan(x) = sin(x) / cos(x), где x — угол.
• Диапазон значений: от -бесконечности до +бесконечности.
• Периодичность: tan(x) = tan(x + π), где π — число Пи.
• Асимптоты: tan(x) имеет вертикальные асимптоты в точках x = (2n + 1) * (π/2), где n — целое число.

Тангенс является важным инструментом для работы с углами и тригонометрическими функциями. Он широко применяется в математике, физике, геометрии, астрономии и других научных и технических дисциплинах.

Соотношение тангенса с другими тригонометрическими функциями

Соотношение тангенса с синусом и косинусом определяется следующим образом:

• tan(x) = sin(x) / cos(x)

Данное соотношение позволяет выразить тангенс через синус и косинус. Оно является основным для решения многих задач и применений в математике и физике.

Соотношение тангенса с котангенсом определяется следующим образом:

• tan(x) = 1 / cot(x)

Котангенс (cot) – это обратная функция к тангенсу. Таким образом, соотношение тангенса и котангенса позволяет выразить одну функцию через другую.

Соотношение тангенса с секансом и косекансом определяется следующим образом:

• tan(x) = 1 / sec(x)
• tan(x) = cosec(x) / 1

Секанс (sec) – это обратная функция к косинусу, а косеканс (cosec) – это обратная функция к синусу. Таким образом, соотношение тангенса с секансом и косекансом также позволяет выразить одну функцию через другую.

Знание соотношения тангенса с другими тригонометрическими функциями позволяет более гибко использовать эту функцию в различных математических и физических задачах, а также оценивать их взаимосвязь и взаимозависимость.

Вопрос-ответ:

Как определить тангенс в математике?

Тангенс — это математическая функция, которая определяется как отношение противолежащего катета к прилежащему катету прямоугольного треугольника. Другими словами, тангенс угла равен отношению противолежащего катета к прилежащему катету.

Какие свойства тангенса в математике?

Тангенс обладает несколькими свойствами. Во-первых, тангенс обратен котангенсу: tg(x) = 1/ctg(x). Во-вторых, тангенс является нечётной функцией, то есть tg(-x) = -tg(x). Также, тангенс периодически повторяется через каждые pi радиан или 180 градусов.

Как применяется тангенс в математике?

Тангенс широко применяется в различных областях математики и естественных наук. В геометрии, тангенс используется для нахождения неизвестных сторон и углов треугольников. В физике, тангенс используется для моделирования колебаний и волн. Тангенс также используется в тригонометрических уравнениях и исследовании графиков функций.

Как найти значение тангенса угла?

Для нахождения значения тангенса угла можно использовать тангенс таблицы значений или калькулятор. Если известны значения противолежащего и прилежащего катетов прямоугольного треугольника, то тангенс угла можно найти как отношение противолежащего катета к прилежащему катету.

Какие другие функции связаны с тангенсом в математике?

С тангенсом связаны также функции котангенс, секанс и косеканс. Котангенс (ctg) — обратная функция к тангенсу, секанс (sec) — обратная функция к косинусу, а косеканс (cosec) — обратная функция к синусу.

Что такое тангенс?

Тангенс (tan) — это тригонометрическая функция, которая определяется как отношение противолежащего катета к прилежащему катету прямоугольного треугольника.

Применение тангенса в геометрии

Тангенс используется для нахождения угла между прямыми, для расчета высоты объектов, а также для определения расстояния между точками на плоскости.

Применение тангенса в геометрии обеспечивает возможность решать разнообразные задачи, связанные с определением углов и расстояний. Например, с помощью тангенса можно определить высоту дерева или здания, если известны длина тени и угол падения солнечных лучей. Также можно найти расстояние между двумя точками на карте, если известны координаты этих точек.

Особенностью тангенса является то, что его значение может быть отрицательным или бесконечно большим. Это объясняется тем, что тангенс определен только для некоторых углов, а его значение зависит от соотношения между сторонами прямоугольного треугольника.

Таким образом, применение тангенса в геометрии позволяет решать различные задачи, связанные с определением углов и расстояний. Знание тангенса и умение его применять помогает геометрам и инженерам решать сложные задачи и строить точные модели объектов.

Применение тангенса в физике

В механике тангенс используется для определения угла наклона наклонной плоскости или наклонного бруска. Также с помощью тангенса можно вычислять момент силы, действующий на вращающееся тело.

В оптике тангенс применяется для определения угла преломления света при прохождении через границу двух сред с разными показателями преломления. Это позволяет рассчитывать путь луча света и его отклонение в разных средах.

В электричестве тангенс используется для расчета электрического сопротивления цепи, состоящей из резисторов. Он также применяется для определения фазовой разности между током и напряжением в электрической цепи.

Тангенс – важная математическая функция, которая находит широкое применение в физике. Она помогает решать различные задачи и делает математические расчеты более точными и эффективными.

Применение тангенса в инженерии и технике

Тангенс определяется как отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике. Таким образом, тангенс угла α можно выразить как отношение стороны, противолежащей углу α, к стороне, прилежащей углу α.

В инженерии и технике тангенс широко используется для решения задач, связанных с измерением и моделированием углов. Например, при проектировании мостов, зданий и других сооружений, инженеры используют тангенс для определения углов наклона поверхностей и расчета устойчивости конструкций.

Тангенс также применяется в электротехнике и физике. В электрических цепях, тангенс угла фазы используется для вычисления реактивного сопротивления и определения эффективности электронных устройств. В оптике, тангенс используется для определения угла падения света на поверхность и расчета преломления лучей.

Кроме того, тангенс находит применение в автоматике и робототехнике. В системах автоматического управления, тангенс угла наклона используется для определения положения объекта и реализации различных алгоритмов стабилизации.

Область примененияПримеры

Строительство	Определение углов наклона поверхностей, расчет устойчивости конструкций
Электротехника	Расчет реактивного сопротивления, определение эффективности электронных устройств
Оптика	Определение угла падения света на поверхность, расчет преломления лучей
Автоматика и робототехника	Определение положения объекта, реализация алгоритмов стабилизации

Таким образом, тангенс является важной математической функцией, которая находит широкое применение в различных областях инженерии и техники. Знание и понимание этой функции позволяет инженерам и техникам решать сложные задачи и создавать инновационные технологии.