Что такое середина отрезка в математике

Середина отрезка в математике — это точка, которая находится на равном расстоянии от концов отрезка. Она является средней точкой между двумя концами отрезка и имеет координаты, равные средним значениям координат концов отрезка. Середина отрезка играет важную роль в геометрии и алгебре, используется для решения различных задач и нахождения других характеристик отрезка, таких как его длина и углы. Понимание концепции середины отрезка является важным элементом в изучении математики и ее приложений.

Середина отрезка – это точка, которая находится на равном удалении от концов данного отрезка. В математике середина отрезка играет важную роль и используется во многих областях, включая геометрию, алгебру и теорию чисел.

Чтобы найти середину отрезка, нужно разделить его на две равные части. Если длина отрезка известна, то координаты середины можно найти по формуле: x = (x1 + x2) / 2, y = (y1 + y2) / 2, где (x1, y1) и (x2, y2) – координаты концов отрезка.

Например, если отрезок AB задан координатами A(2, 4) и B(6, 8), то координаты середины отрезка можно найти следующим образом: x = (2 + 6) / 2 = 4, y = (4 + 8) / 2 = 6. Таким образом, середина отрезка AB имеет координаты (4, 6).

Середина отрезка также является центром симметрии отрезка. Это означает, что отрезок AB и отрезок MB (где M – середина отрезка AB) равны по длине и параллельны друг другу.

Определение середины отрезка

Для нахождения середины отрезка можно использовать следующую формулу:

середина отрезка = (координата_точки_А + координата_точки_В) / 2

Например, если дан отрезок АВ с координатами А(2, 3) и В(6, 9), то середина отрезка будет:

середина отрезка = (2 + 6) / 2 = 4

Таким образом, середина отрезка АВ будет иметь координаты (4, 6).

Геометрическое представление середины отрезка

Геометрическое представление середины отрезка в математике обозначает точку, которая расположена на равном расстоянии от концов данного отрезка. Для наглядности, можно представить отрезок как прямую линию на плоскости, где концы отрезка отмечены точками. Серединой отрезка будет точка, которая делит данный отрезок на две равные части, как по длине, так и по положению.

Для определения середины отрезка, можно использовать геометрический метод. Для этого необходимо провести линию, которая соединяет концы отрезка, и найти точку пересечения этой линии с отрезком. Именно эта точка и будет являться серединой отрезка.

Пример:

Рассмотрим отрезок AB на плоскости, где A(-2, 1) и B(4, 5). Чтобы найти середину отрезка, проведем линию, соединяющую точки A и B. Найдем точку пересечения этой линии с отрезком AB. В результате получим точку M(1, 3), которая будет являться серединой отрезка AB.

Таким образом, геометрическое представление середины отрезка позволяет наглядно определить точку, которая делит отрезок на две равные части.

Координаты середины отрезка в декартовой системе координат

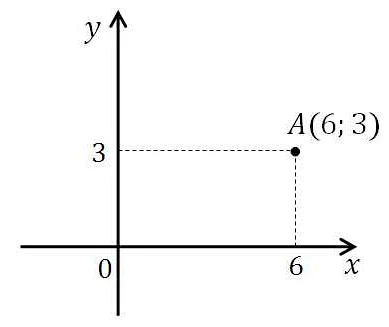
Пусть дан отрезок AB с координатами точек A(x1, y1) и B(x2, y2). Тогда координаты середины отрезка M(x, y) можно найти по следующим формулам:

x = (x1 + x2) / 2

y = (y1 + y2) / 2

Например, пусть дан отрезок AB с координатами точек A(2, 3) и B(6, 7). Тогда координаты середины отрезка M можно найти следующим образом:

x = (2 + 6) / 2 = 4

y = (3 + 7) / 2 = 5

Таким образом, координаты середины отрезка AB равны M(4, 5).

Нахождение середины отрезка по формуле

Середину отрезка можно найти с помощью формулы. Формула для нахождения середины отрезка выглядит следующим образом:

Если заданы координаты начальной точки A(x1, y1) и конечной точки B(x2, y2), то середина отрезка M(x, y) находится по формулам:

• x = (x1 + x2) / 2
• y = (y1 + y2) / 2

То есть, чтобы найти x-координату середины отрезка, нужно сложить x-координаты начальной и конечной точек, а затем разделить полученную сумму на 2. Аналогично для y-координаты.

Например, пусть дан отрезок AB с начальной точкой A(2, 4) и конечной точкой B(8, 10). Чтобы найти середину отрезка, подставим значения координат в формулы:

• x = (2 + 8) / 2 = 10 / 2 = 5
• y = (4 + 10) / 2 = 14 / 2 = 7

Таким образом, середина отрезка AB имеет координаты M(5, 7).

Середина отрезка в теории вероятности

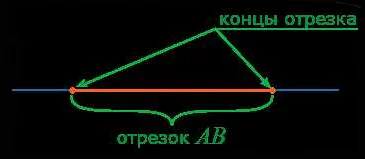
В теории вероятности середина отрезка играет важную роль при решении различных задач. Она позволяет найти точку, которая делит отрезок на две равные части и имеет равные вероятности попасть в каждую из них.

Для определения середины отрезка в теории вероятности можно использовать следующую формулу:

Формула для нахождения середины отрезка

xсред = (a + b) / 2

Где xсред — середина отрезка, a — начало отрезка, b — конец отрезка.

Пример:

ОтрезокСередина отрезка

Отрезок [0, 10]	5
Отрезок [2, 8]	5

Таким образом, середина отрезка в теории вероятности позволяет найти точку, которая делит отрезок на две равные части и является вероятностной серединой. Это важное понятие, используемое при решении задач вероятности.

Видео по теме:

Вопрос-ответ:

Что такое середина отрезка в математике?

Середина отрезка — это точка, которая делит отрезок на две равные части.

Как найти середину отрезка?

Чтобы найти середину отрезка, нужно найти среднее арифметическое координат концов отрезка.

Можно ли найти середину отрезка, если не известны его координаты?

Нет, для того чтобы найти середину отрезка, необходимо знать координаты его концов.

Какие свойства имеет середина отрезка?

Середина отрезка является его центром симметрии, то есть относительно середины отрезка можно провести ось симметрии, на которой точки отрезка будут симметричны относительно середины.

Какие примеры можно привести для середины отрезка?

Примеры середин отрезков: середина отрезка с концами в точках (0,0) и (4,0) имеет координаты (2,0); середина отрезка с концами в точках (1,3) и (5,7) имеет координаты (3,5).

Примеры нахождения середины отрезка

Середина отрезка может быть найдена с помощью формулы:

Середина отрезка = (координата точки A + координата точки B) / 2

Например, у нас есть отрезок AB, где A(3, 4) и B(7, 10).

Для нахождения середины отрезка, нужно сложить координаты точки A и точки B, а затем разделить результат на 2:

Середина отрезка = ((3 + 7) / 2, (4 + 10) / 2) = (10 / 2, 14 / 2) = (5, 7)

Таким образом, середина отрезка AB с координатами A(3, 4) и B(7, 10) будет иметь координаты (5, 7).

Значение середины отрезка в практических задачах

Один из примеров применения середины отрезка – это нахождение среднего значения двух чисел. Если у нас есть два числа, то середина между ними будет являться средним значением этих чисел. Например, если у нас есть отрезок с конечными точками 2 и 6, то его середина будет равна (2 + 6) / 2 = 4.

Второй пример применения середины отрезка – это нахождение среднего значения в наборе данных. Если у нас есть набор чисел, мы можем найти середину этого набора, добавив все числа и разделив сумму на их количество. Например, если у нас есть набор чисел {1, 3, 5, 7, 9}, то середина этого набора будет равна (1 + 3 + 5 + 7 + 9) / 5 = 5.

Третий пример применения середины отрезка – это нахождение середины временного промежутка. Если у нас есть временной промежуток, мы можем найти его середину, используя начальную и конечную дату. Например, если временной промежуток начинается в 10:00 и заканчивается в 14:00, то его середина будет равна 12:00.

Таким образом, понимание значения середины отрезка позволяет решать различные практические задачи, связанные с нахождением средних значений числовых данных или временных промежутков.