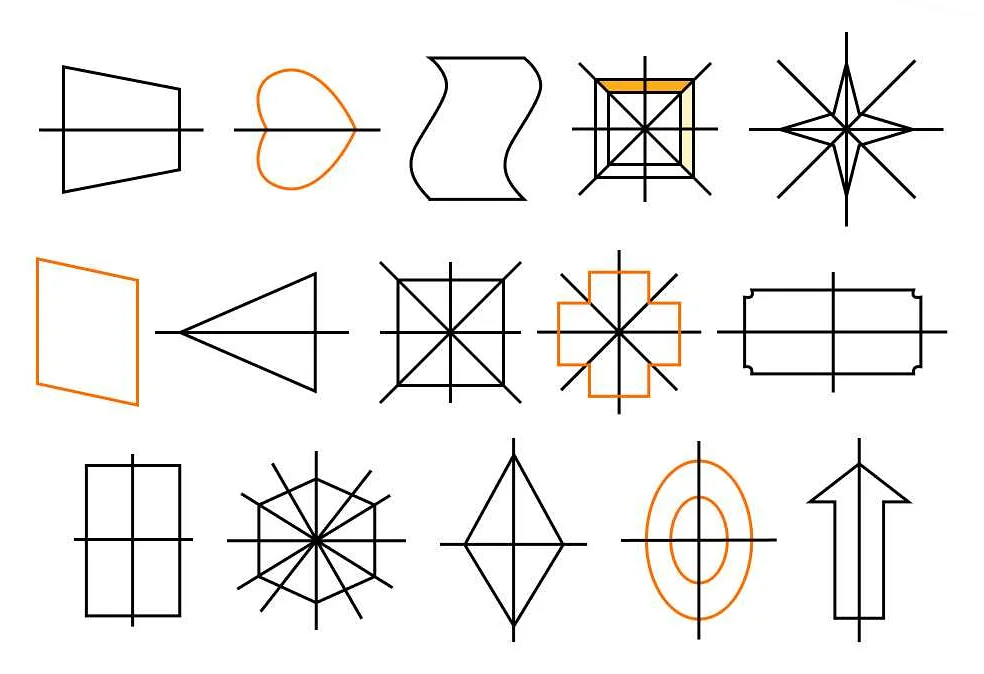Что такое симметрия в математике 2 класс рисунок квадрата

Симметрия в математике 2 класс — это особое свойство фигур и объектов, при котором они могут быть разделены на две одинаковые части. Рисунок квадрата поможет наглядно представить детям этот концепт и понять, какие фигуры являются симметричными.

Симметрия — одно из важнейших понятий в математике, которое помогает нам понимать и описывать различные формы и объекты. Симметрия включает в себя идею равенства или соответствия двух частей объекта относительно некоторой оси, точки или плоскости. В математике симметрия играет важную роль и широко используется для решения задач и анализа геометрических форм.

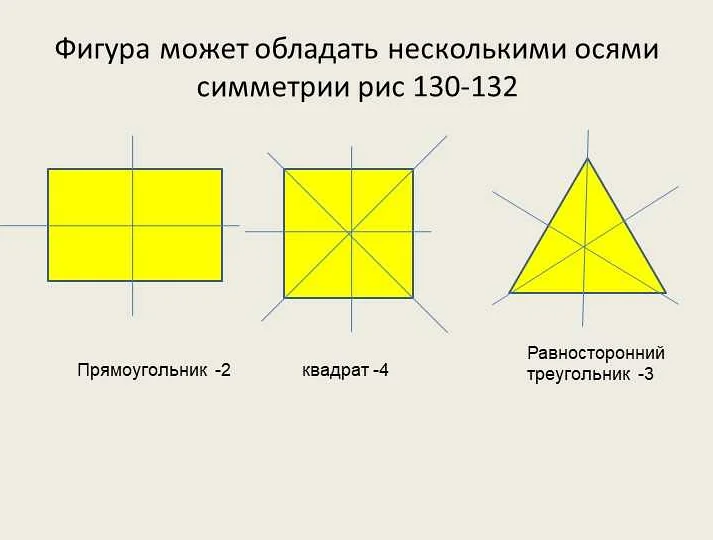
Рисунок квадрата — отличный пример, который помогает детям понять и запомнить понятие симметрии. Квадрат имеет четыре стороны, и каждая из них является осью симметрии. Это означает, что если мы разделим квадрат пополам по одной из его сторон, то две полученные половинки будут точно совпадать.

Симметричные фигуры — это фигуры, которые одинаковы относительно некоторой оси симметрии. Например, если мы возьмем квадрат и нарисуем его отражение, то получим другой квадрат, который будет абсолютно идентичен исходному.

Важно учитывать, что симметрия может быть не только вертикальной, но и горизонтальной или диагональной. Это означает, что можно провести ось симметрии не только вертикально, но и горизонтально или по диагонали квадрата. Таким образом, симметрия открывает перед нами широкие возможности для изучения и анализа геометрических форм и фигур.

Изучение симметрии в математике помогает детям развивать логическое мышление, образное и геометрическое представление. Оно также помогает им развивать умение анализировать и описывать различные объекты с точки зрения их симметрии и формы. Рисунок квадрата — это отличный пример, который помогает детям запомнить и понять понятие симметрии и применять его на практике.

Что такое симметрия:

Видео по теме:

Ось симметрии:

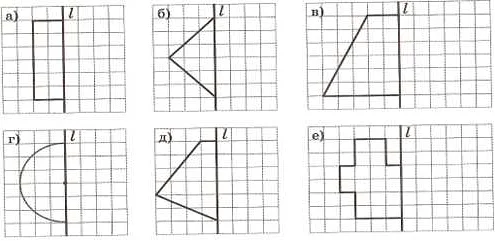
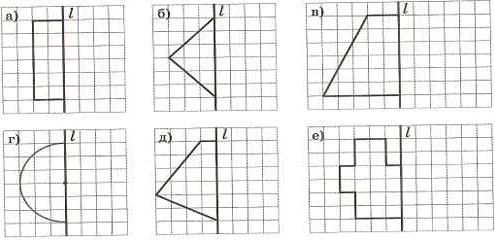
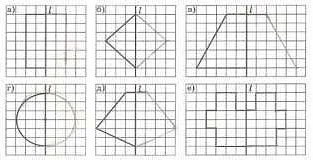
Для того чтобы понять, что фигура имеет ось симметрии, можно воспользоваться методом «сложи-получи». Если при сложении двух половин фигуры они точно совпадают, то это означает, что фигура обладает осью симметрии.

Ось симметрии имеет важное значение в геометрии и дизайне. Она помогает создавать сбалансированные и гармоничные образы. Знание о оси симметрии позволяет анализировать и создавать различные фигуры и узоры.

Симметрия в рисунке квадрата:

Например, если мы нарисуем квадрат с каким-то рисунком, а затем проведем вертикальную линию посередине, то обе ее части будут выглядеть одинаково. Это означает, что рисунок в квадрате обладает симметрией относительно вертикальной оси.

То же самое верно и для симметрии относительно горизонтальной оси. Если мы проведем горизонтальную линию посередине квадрата, обе ее части будут выглядеть одинаково.

Симметрия в рисунке квадрата имеет особое значение, так как помогает нам увидеть и понять определенные закономерности и особенности формы и структуры. Кроме того, она может быть использована при создании симметричных рисунков или при решении различных задач и головоломок.

Таким образом, симметрия в рисунке квадрата — это интересное математическое свойство, которое помогает нам лучше понять и визуализировать различные аспекты формы и структуры.

Как определить симметричные фигуры:

1. Взгляните на фигуру и найдите ось симметрии. Ось симметрии — это линия, которая разделяет фигуру на две одинаковые части.

2. Проверьте, что обе части фигуры выглядят полностью одинаково. Это означает, что каждая часть должна иметь одинаковую форму, размер и расположение элементов.

3. Если найдена ось симметрии и обе части фигуры выглядят одинаково, то фигура является симметричной.

Например, круг имеет бесконечное количество осей симметрии. По любой линии, проходящей через его центр, круг делится на две половины, которые выглядят одинаково. Квадрат также является симметричным, так как его можно разделить на две половины, которые отражаются относительно вертикальной и горизонтальной осей симметрии.

Симметричные фигуры в природе:

Природа полна примеров симметрии. Множество живых организмов обладают симметричной структурой, что делает их более эстетически привлекательными и функциональными. Например, лицо человека обычно имеет симметричную форму, где левая и правая половины равны и зеркально отражены друг относительно центральной оси. Также многие растения имеют симметричные лепестки, листья или плоды.

Симметричные фигуры в природе не только привлекательны, но и играют важную роль в их функционировании. Например, симметричная форма позволяет организмам лучше передвигаться и находить пищу, а также облегчает привлечение партнеров для размножения.

Кроме того, симметрия также проявляется в геометрических формах природных объектов. Например, снежинка — это классический пример симметричной фигуры. Ее шестиугольная форма симметрично повторяется вокруг центральной оси, создавая красивый и сложный узор.

Таким образом, симметрия в природе играет важную роль и является одним из основных принципов, определяющих формы и структуры живых и неживых объектов.

Зачем изучать симметрию:

• Симметрия помогает нам понять и описать формы и фигуры, которые мы видим вокруг себя.
• Она помогает нам создавать красивые и гармоничные дизайны, как в искусстве, так и в архитектуре.
• Изучение симметрии помогает развивать наше пространственное мышление и логическое мышление.
• Она помогает нам решать задачи и находить решения для сложных проблем.
• Симметрия также имеет важное значение в науке и технологии, например, в кристаллографии и оптике.

Изучение симметрии не только интересно, но и полезно для нашего развития и понимания мира вокруг нас.

Примеры симметрии в повседневной жизни:

1. Лицо человека: Человеческое лицо обладает симметрией, так как правая половина лица симметрична левой половине. Например, глаза, нос, уши и другие части лица находятся в симметричном положении.

2. Растения: Некоторые растения также имеют симметрию. Например, цветок розы имеет радиальную симметрию, где лепестки располагаются симметрично относительно центра цветка.

3. Бабочки: Крылья бабочек обычно имеют симметричную структуру, где одна половина крыла симметрична другой половине.

4. Фрукты и овощи: Некоторые фрукты и овощи имеют симметричную форму. Например, яблоко и груша имеют сферическую симметрию, где любая прямая линия, проходящая через центр фрукта, делит его на две симметричные половины.

5. Здания: Некоторые архитектурные сооружения имеют симметричные формы. Например, симметричные фасады зданий, где линии и элементы декора симметрично расположены относительно вертикальной оси здания.

6. Зеркала: Зеркала являются примером идеальной симметрии, где отражение в зеркале полностью повторяет изображение и делит его на две симметричные части.

7. Машины: Некоторые автомобили и другие машины имеют симметричную форму. Например, линии и формы кузовов многих автомобилей симметричны относительно вертикальной оси.

8. Часы: Часы симметричны относительно центра, где стрелки делают симметричные движения вокруг оси циферблата.

9. Украшения: Некоторые украшения, такие как серьги, браслеты и кольца могут иметь симметричную форму или узоры.

10. Музыка: Музыка может иметь симметричные структуры, например, мелодии или ритмы, которые повторяются и создают симметричные паттерны.

Присутствие симметрии в повседневной жизни показывает, что концепция симметрии в математике имеет широкое применение и отражает реальные явления и структуры в окружающем мире.

Вопрос-ответ:

Что такое симметрия в математике?

Симметрия в математике — это свойство фигуры или объекта, при котором он может быть разделен на две равные части, которые совпадают друг с другом при отражении. То есть, если мы возьмем фигуру и отразим ее относительно некоторой оси, то получим две равные половины.

Как определить симметричную фигуру?

Чтобы определить, является ли фигура симметричной, нужно найти ось симметрии. Это такая линия или плоскость, при отражении относительно которой фигура совпадает сама с собой. Если ось симметрии найдена, фигуру можно разделить на две равные половины, которые будут зеркальным отражением друг друга.

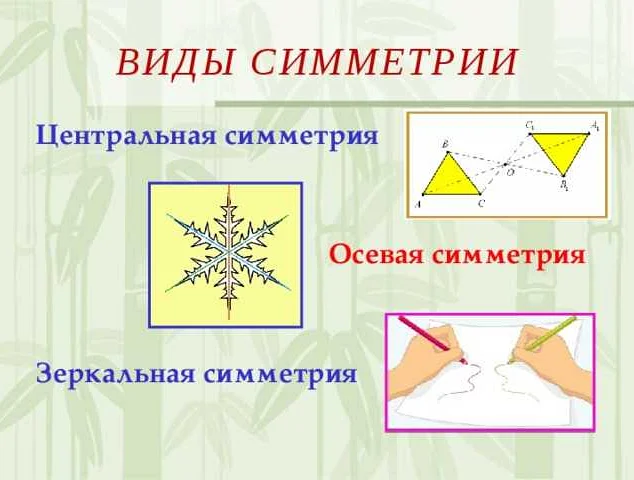
Какие виды симметрии бывают?

В математике существует несколько видов симметрии. Один из них — осевая симметрия, когда фигура имеет ось симметрии, относительно которой ее можно разделить на две равные половины. Еще один вид — центральная симметрия, когда фигура имеет центр симметрии, и все ее точки равноудалены от этого центра.

Какие примеры симметричных фигур можно привести?

Примерами симметричных фигур могут служить круг, квадрат, прямоугольник, треугольник и многоугольники. Например, квадрат является симметричной фигурой, так как его можно разделить на две равные половины, отраженные относительно горизонтальной и вертикальной осей.

Как можно объяснить симметрию на примере рисунка квадрата?

Мы можем объяснить симметрию на примере рисунка квадрата следующим образом: если мы возьмем квадрат и отразим его относительно вертикальной оси, то получим две половины квадрата, которые будут зеркальным отражением друг друга. То есть, левая половина будет совпадать с правой. Также, если мы отразим квадрат относительно горизонтальной оси, получим две равные половины, которые будут зеркальными отражениями друг друга — верхняя половина будет совпадать с нижней.

Что такое симметрия?

Симметрия — это особое свойство фигуры, которое означает, что она может быть разделена на две половины, которые идентичны или почти идентичны друг другу. Если мы сложим одну половину фигуры на другую, они полностью совпадут.