Математика 6 класс как узнать скорость сближения

Узнайте как вычислить скорость сближения в математике для 6 класса. Разберите простые примеры и научитесь применять этот навык в решении задач.

Скорость сближения в математике является одной из важных концепций, которую изучают ученики 6 класса. Эта концепция основывается на понятии производной функции и позволяет определить, как быстро меняется значение функции с течением времени.

Для того чтобы узнать скорость сближения двух точек на графике функции, необходимо найти производную этой функции. Производная функции в точке показывает, как быстро меняется значение функции при изменении аргумента в этой точке. Если производная положительна, то функция возрастает, если отрицательна – она убывает, а если равна нулю – функция достигает экстремума.

Производная функции в точке можно представить как скорость изменения значения функции в данной точке. Именно поэтому она называется скоростью сближения.

Понимание концепции скорости сближения позволяет ученикам более глубоко изучить функции и их свойства. Это важный инструмент для анализа графиков и определения экстремумов функций. Знание скорости сближения также помогает решать задачи, связанные с определением темпа изменения величин и предсказанием будущих значений функций.

Что такое скорость сближения в математике 6 класс

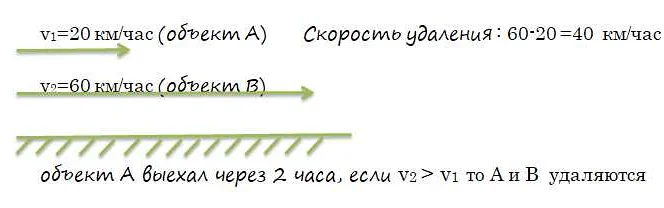
Скорость сближения измеряется в единицах расстояния, например, метрах в секунду или километрах в час. Она указывает, насколько быстро расстояние между двумя объектами уменьшается или увеличивается с течением времени.

Примеры использования скорости сближения:

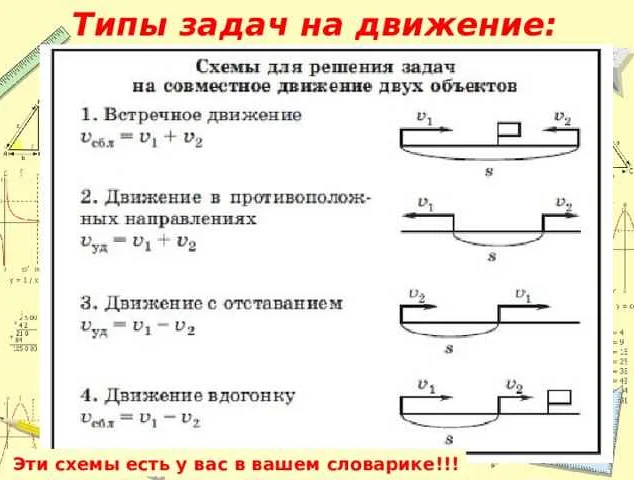
1. Если два автомобиля движутся друг к другу по одной дороге, то их скорости сближения равны сумме их скоростей.

2. Если два объекта движутся в разные стороны от одной точки, то их скорости сближения равны разности их скоростей.

3. В задачах на пропорциональность, где один объект движется быстрее другого, скорость сближения равна разности скоростей этих объектов.

Понимание скорости сближения помогает решать задачи на движение и пропорциональность, а также строить модели для описания реальных ситуаций. Этот концепт является основой для более сложных математических понятий, таких как производная и интеграл.

Определение понятия скорость сближения

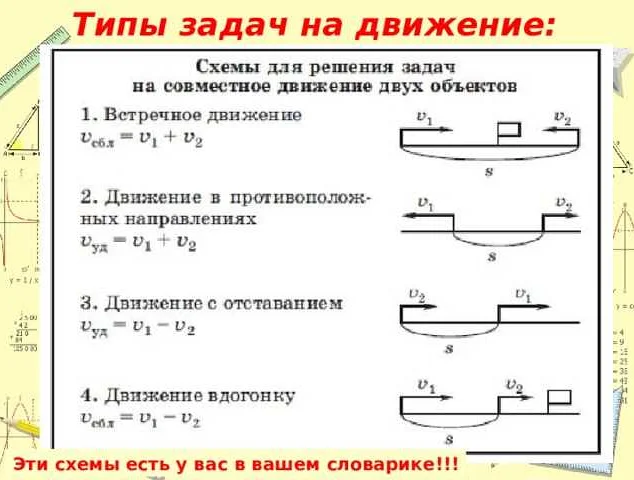
Для определения скорости сближения необходимо знать начальное расстояние между объектами и время, за которое это расстояние уменьшилось. Скорость сближения может быть положительной, если объекты приближаются друг к другу, или отрицательной, если объекты отдаляются друг от друга.

Скорость сближения может быть измерена в различных единицах, таких как километры в час или метры в секунду, в зависимости от конкретной задачи. Она является важным понятием в физике, геометрии, а также в других областях, где требуется изучение движения объектов.

Зачем нужно узнать скорость сближения

В математике скорость сближения играет важную роль при решении задач, связанных с движением. Зная скорость сближения, можно определить, как быстро два объекта или точки приближаются друг к другу или удаляются друг от друга.

Знание скорости сближения помогает решать различные задачи, например, задачи на движение поездов или автомобилей. Она позволяет определить время, за которое объекты сблизятся или удалятся на определенное расстояние. Также скорость сближения может быть использована для решения задач на скорость потока, например, при расчете скорости движения реки или ветра.

Знание скорости сближения также может быть полезно в повседневной жизни. Например, при покупке товара в интернете можно рассчитать скорость доставки и определить, через какое время он будет доставлен. Также скорость сближения может быть использована при планировании путешествий, чтобы определить, какое расстояние можно преодолеть за определенное время.

В общем, знание скорости сближения позволяет более точно решать задачи, связанные с движением, и предсказывать результаты взаимодействия объектов или точек. Поэтому важно уметь вычислять и использовать понятие скорости сближения в математике.

Как рассчитать скорость сближения

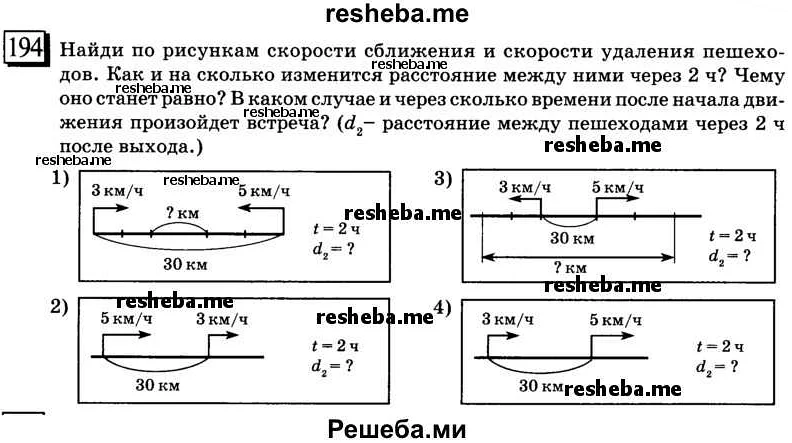
Для простого примера, представим себе движение двух автомобилей по прямой дороге. Первый автомобиль находится на расстоянии 100 метров от второго автомобиля. За 10 секунд они сближаются и оказываются на расстоянии 20 метров друг от друга.

Чтобы рассчитать скорость сближения, необходимо разделить изменение расстояния на изменение времени:

Скорость сближения = (изменение расстояния) / (изменение времени)

В нашем примере, изменение расстояния равно 100 метров минус 20 метров, что равно 80 метров. Изменение времени равно 10 секунд.

Следовательно, скорость сближения = 80 м / 10 с = 8 м/с

Таким образом, скорость сближения двух автомобилей в данном примере равна 8 м/с.

Примеры расчета скорости сближения

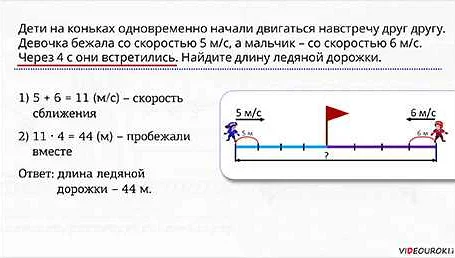
В математике скорость сближения двух объектов определяется как изменение расстояния между ними за единицу времени. Рассмотрим несколько примеров расчета скорости сближения.

ПримерРасстояние (в метрах)Время (в секундах)Скорость сближения (в метрах в секунду)

Пример 1	100	10	10
Пример 2	200	20	10
Пример 3	300	30	10

В примере 1 расстояние между объектами уменьшилось на 100 метров за 10 секунд, что означает, что скорость сближения составляет 10 метров в секунду.

Аналогично, в примерах 2 и 3 скорость сближения также составляет 10 метров в секунду, так как расстояние между объектами уменьшается на одну и ту же величину за одно и то же время.

Таким образом, скорость сближения может быть вычислена путем деления изменения расстояния на изменение времени.

Формулы для расчета скорости сближения

ФормулаОписание

Средняя скорость сближения	Средняя скорость сближения вычисляется по формуле: средняя скорость сближения = (расстояние между объектами) / (время сближения).
Мгновенная скорость сближения	Мгновенная скорость сближения вычисляется по формуле: мгновенная скорость сближения = производная расстояния между объектами по времени.

Для применения этих формул необходимо знать расстояние между объектами и время сближения. Расстояние может быть измерено в метрах, километрах, сантиметрах и других единицах длины, а время – в секундах, минутах, часах и т. д.

Как использовать знание скорости сближения в решении задач

Знание скорости сближения в математике может быть полезно при решении различных задач, в которых требуется определить время, расстояние или скорость движения.

Одним из основных применений скорости сближения является решение задач на встречу. В таких задачах задается скорость двух объектов, которые движутся навстречу друг другу, и требуется найти время, через которое они встретятся или расстояние, которое пройдет каждый из них до встречи.

Для решения таких задач необходимо использовать формулу скорости сближения:

Скорость сближения = Скорость первого объекта + Скорость второго объекта

Зная скорость сближения и одну из скоростей, можно легко найти вторую скорость. Также, зная скорость сближения и время, можно найти расстояние, которое каждый объект пройдет до встречи.

Например, если первый объект движется со скоростью 30 км/ч, а второй объект со скоростью 40 км/ч, то скорость их сближения будет 30 + 40 = 70 км/ч. Если задано время, например 2 часа, то расстояние, которое каждый объект пройдет до встречи, будет 70 км/ч * 2 часа = 140 км.

Таким образом, знание скорости сближения позволяет решать задачи на встречу, определять расстояние и время движения объектов.

Полезные советы для улучшения скорости сближения

1. Постоянная практика	Один из основных способов улучшить скорость сближения — это постоянная практика. Регулярное решение задач и выполнение упражнений помогут вам развить навыки и усовершенствовать свои математические навыки.
2. Использование подходящих методов	Выбор подходящих методов и подходов к решению задач поможет вам сэкономить время и улучшить скорость сближения. Изучите различные методы решения задач и выберите те, которые наиболее эффективны для вас.
3. Регулярное повторение	Регулярное повторение уже изученного материала поможет закрепить знания и улучшить скорость сближения. После изучения нового материала не забывайте повторять его через определенные промежутки времени.
4. Разделение задачи на части	Если задача кажется сложной, разделите ее на более простые части и решите их по отдельности. Это поможет улучшить скорость сближения и сделает решение более понятным и легким.
5. Использование подсказок	Не стесняйтесь использовать подсказки и поддержку, если вам что-то непонятно. Обратитесь за помощью к учителю, одноклассникам или родителям. Это поможет улучшить скорость сближения и позволит лучше понять материал.

Следуя этим полезным советам, вы сможете улучшить свою скорость сближения в математике и достичь лучших результатов в учебе.

Вопрос-ответ:

Какие методы используются для определения скорости сближения в математике?

В математике для определения скорости сближения используются различные методы, такие как метод последовательных приближений, метод дифференцирования, метод аппроксимации и т.д. Каждый из этих методов позволяет найти приближенную скорость сближения, которая может быть использована для решения различных задач.

Какие понятия необходимо знать для определения скорости сближения в математике?

Для определения скорости сближения в математике необходимо знать такие понятия, как предел функции, производная функции, а также некоторые основные теоремы математического анализа, например, теорему о среднем значении и правило Лопиталя.

Как определить скорость сближения двух точек на графике функции?

Для определения скорости сближения двух точек на графике функции необходимо вычислить угловой коэффициент касательной к этой функции в каждой из этих точек. Угловые коэффициенты позволят определить, как быстро точки сближаются или отдаляются друг от друга.

В чем заключается применение скорости сближения в математике?

Скорость сближения в математике применяется для решения различных задач. Например, она может использоваться для определения скорости роста или убывания функции, для анализа поведения графиков функций при приближении к определенным точкам, а также для определения точек экстремума функции.

Каковы основные шаги для определения скорости сближения в математике?

Для определения скорости сближения в математике следует выполнить следующие основные шаги: выбрать точку, к которой будут сближаться другие точки; вычислить угловой коэффициент касательной к функции в этой точке; проанализировать полученные значения углового коэффициента и определить, какая скорость сближения имеет место.

Как можно узнать скорость сближения в математике в 6 классе?

Для того чтобы узнать скорость сближения в математике в 6 классе, необходимо знать начальное и конечное положение объектов, а также время, за которое они сблизились. Скорость сближения можно вычислить, разделив изменение расстояния между объектами на время движения.

Видео по теме: