Значение и примеры использования смешанного числа в математике для учащихся 5 класса

Смешанное число — это число, состоящее из целой части и дробной части. В математике 5 класса, смешанные числа используются для представления нецелых чисел. Примеры смешанных чисел и их использование в задачах.

Смешанное число — это число, которое представляет собой сумму натурального числа и десятичной дроби. Оно состоит из целой части и дробной части, разделенных знаком плюс или минус.

Например, смешанным числом может быть 3 1/4 или -2 3/5. В этих числах число перед дробной частью (например, 3 или -2) называется целой частью, а число после дробной части (например, 1/4 или 3/5) называется дробной частью.

Для работы с смешанными числами, важно знать, как их записывать, как выполнять операции сложения, вычитания, умножения и деления. Также необходимо уметь преобразовывать смешанные числа в неправильные дроби и наоборот.

На уроках математики в 5 классе, ученикам предлагается решать задачи, где необходимо использовать смешанные числа. Знание и понимание этой темы поможет им успешно справляться с заданиями и улучшать свои навыки в математике.

Определение смешанного числа в математике

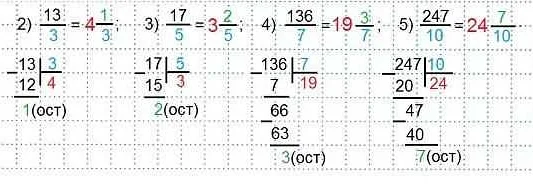
Например, число 3 1/2 является смешанным числом. Здесь целая часть равна 3, а дробная часть равна 1/2.

Смешаное число можно представить в виде десятичной дроби, сложив целую и дробную части. В примере с числом 3 1/2, сначала нужно перевести дробную часть в десятичную дробь: 1/2 = 0.5. Затем складываем целую и десятичную части: 3 + 0.5 = 3.5.

Смешаное число можно также представить в виде обыкновенной дроби. Для этого нужно умножить целую часть на знаменатель дроби и прибавить числитель дробной части. В примере с числом 3 1/2, мы получим дробь (3 * 2 + 1)/2 = 7/2.

Смешаные числа часто используются в повседневной жизни, например, при измерении времени или расстояния. Они позволяют удобно записывать и работать с числами, которые не являются целыми, но имеют целую часть.

Понятие и особенности

Основной особенностью смешанного числа является то, что оно может быть представлено как целое число и дробь одновременно. Например, смешанное число 3 1/2 означает, что у нас есть три целых единицы и половина единицы.

Смешанные числа могут быть положительными или отрицательными. В случае отрицательного смешанного числа знак минус ставится перед целой частью. Например, -2 3/4 означает, что у нас есть два целых числа минус четверть числа.

Смешанные числа часто используются для представления нецелых величин, таких как временные интервалы, длины и объемы. Они удобны в использовании и позволяют более точно выразить и сравнивать значения.

Как представить смешанное число

Для представления смешанного числа в математике 5 класса мы используем обыкновенные дроби. Например, если у нас есть смешанное число 3 1/2, то его можно записать в виде обыкновенной дроби 7/2. В данном примере целая часть равна 3, а дробная часть равна 1/2. Чтобы получить обыкновенную дробь, мы умножаем целую часть на знаменатель дроби и прибавляем числитель дроби. Затем знаменатель дроби остается таким же, а числитель полученной обыкновенной дроби равен сумме числителя дроби и произведения целой части на знаменатель дроби.

Итак, чтобы представить смешанное число в виде обыкновенной дроби:

• Умножаем целую часть на знаменатель дроби
• Прибавляем числитель дроби

Например, для смешанного числа 3 1/2:

Целая часть 3, дробная часть 1/2

7/2 = (3 * 2) + 1 = 7

Таким образом, смешанное число 3 1/2 равно обыкновенной дроби 7/2.

Примеры смешанного числа

Вот несколько примеров смешанного числа:

Целая частьДесятичная частьСмешанное число

2	0.25	2 1/4
5	0.75	5 3/4
3	0.5	3 1/2
8	0.125	8 1/8

В этих примерах, целая часть представляет количество целых единиц, а десятичная часть – долю от целой единицы. Смешанное число показывает, сколько целых единиц и сколько долей дополнительно представлено.

Как выполнять операции с смешанными числами

Чтобы выполнить операции с смешанными числами, нужно сначала привести их к общему знаменателю. Для этого следует найти наименьшее общее кратное (НОК) знаменателей дробных частей и заменить дробные части эквивалентными дробями с общим знаменателем.

После приведения к общему знаменателю можно выполнять операции с целыми и дробными частями отдельно. Например, для сложения смешанных чисел нужно сложить их целые части и дробные части отдельно.

После выполнения операций с целыми и дробными частями, если возможно, следует упростить полученный результат. Например, можно сократить дробную часть, если она имеет общие делители с целой частью.

Не забывайте, что при выполнении операций с смешанными числами результат также будет смешанным числом. Если дробная часть превышает единицу, то ее следует преобразовать в целую часть и оставшуюся дробь записать после нее.

Например, при выполнении операции 3 1/2 + 2 3/4 мы должны сначала привести дробные части к общему знаменателю: 1/2 + 3/4 = 2/4 + 3/4 = 5/4. Затем мы складываем целые части: 3 + 2 = 5. И, наконец, мы преобразуем дробную часть 5/4 в смешанное число: 5/4 = 1 1/4. Полученный результат будет равен 5 1/4.

Таким образом, для выполнения операций с смешанными числами нужно привести их к общему знаменателю, выполнить операции с целыми и дробными частями отдельно, упростить результат и преобразовать его в смешанное число, если это необходимо.

Преобразование смешанного числа в неправильную дробь

Смешанное число представляет собой сумму целой части и дробной части, записанную в виде целого числа и обыкновенной дроби. Например, смешанное число 3 1/2 состоит из целой части 3 и дробной части 1/2.

Чтобы преобразовать смешанное число в неправильную дробь, необходимо выполнить следующие действия:

1. Умножьте целую часть на знаменатель дробной части.
2. Прибавьте полученное произведение к числителю дробной части.
3. Результатом будет неправильная дробь, в которой числитель равен сумме произведения и числителя дробной части, а знаменатель остается неизменным.

Например, для смешанного числа 3 1/2:

3 * 2 = 6

6 + 1 = 7

Таким образом, смешанное число 3 1/2 можно преобразовать в неправильную дробь 7/2.

Преобразование смешанного числа в неправильную дробь позволяет более удобно выполнять арифметические операции с этим числом, а также использовать его в различных математических задачах.

Смешанное число в математике 5 класс: применение

Одно из основных применений смешанных чисел — измерение длины, массы, времени и других физических величин. Например, если мы имеем 3 метра и 50 сантиметров, то мы можем записать это как смешанное число: 3 метра и 50 сантиметров.

Смешанные числа также используются для сравнения величин. Например, если у нас есть два смешанных числа: 2 метра и 30 сантиметров, и 3 метра и 10 сантиметров, мы можем сравнить их, чтобы определить, какое из чисел больше.

Смешанные числа также могут быть использованы для выполнения арифметических операций. Например, мы можем сложить два смешанных числа или умножить смешанное число на целое число.

Важно уметь правильно записывать и читать смешанные числа, чтобы избежать ошибок при решении задач. Запись смешанного числа должна быть удобной и понятной, чтобы можно было легко выполнять операции над ними.

В заключение, смешанные числа являются важным инструментом в математике 5 класса. Они позволяют измерять и сравнивать величины, а также выполнять арифметические операции. Навык работы со смешанными числами поможет ученикам успешно решать задачи, связанные с измерениями и сравнением величин.

Закрепление знаний: задачи на смешанные числа

Чтобы закрепить свои знания о смешанных числах, можно решать различные задачи, которые помогут вам лучше понять их суть и применение в математике.

Ниже приведены несколько примеров задач на смешанные числа, которые помогут вам лучше разобраться в этой теме:

1. В школьной столовой для обеда было приготовлено 5 целых пицц. Каждая пицца разрезалась на 8 равных частей, но ученики успели съесть только 17 частей пиццы. Сколько пицц осталось?
2. В книжном магазине продавались 3 целых книги. Каждая книга стоила 120 рублей. Вам удалось купить только одну книгу, заплатив ровно 100 рублей. Сколько денег вам вернули?
3. В магазине продавались 4 целых и 3/4 килограмма яблок. Один килограмм яблок стоил 80 рублей. Сколько рублей вы заплатите за все эти яблоки?

При решении задач на смешанные числа важно уметь правильно складывать, вычитать, умножать и делить целые числа и дроби. Также необходимо уметь использовать знаки операций и правильно применять их в контексте задачи.

Задачи на смешанные числа помогут вам лучше понять, как применять эти числа в реальной жизни, например, при расчете цен на товары в магазинах или при дележе пиццы на равные части.

Решение каждой задачи на смешанные числа требует внимательности, точности и понимания математических операций. Постепенно вы сможете все лучше разбираться в этой теме и успешно решать задачи на смешанные числа.

Вопрос-ответ:

Как определить, что число является смешанным числом?

Смешанное число представляет собой комбинацию целой части и дробной части. Определить, что число является смешанным, можно, если оно записано в форме «целая часть + дробь». Например, число 3 1/2 является смешанным числом.

Какие примеры смешанных чисел можно привести?

Примеры смешанных чисел: 2 3/4, 1 1/2, 4 2/5 и т.д. Это числа, где есть целая часть и дробная часть.

Как можно записать смешанное число в виде неправильной дроби?

Чтобы записать смешанное число в виде неправильной дроби, нужно умножить целую часть на знаменатель дроби, а затем прибавить числитель. Например, для числа 3 1/2, неправильная дробь будет выглядеть так: (3*2 + 1)/2 = 7/2.

Как можно привести пример задачи с использованием смешанного числа?

Например, задача может быть такой: У Маши было 2 3/4 кг яблок. Она съела 1/2 кг. Сколько яблок осталось у Маши? Для решения этой задачи нужно вычесть количество съеденных яблок от общего количества яблок. То есть, 2 3/4 — 1/2 = 2 1/4 кг яблок осталось у Маши.

Видео по теме: