Пропорция математика как решать
Содержимое
- 1 Пропорция математика как решать
- 1.1 Что такое пропорции в математике?
- 1.2 Основные понятия и определения
- 1.3 Как решать пропорции с помощью кросс-метода?
- 1.4 Примеры решения пропорций
- 1.5 Как использовать пропорции в реальной жизни?
- 1.6 Пропорции в графиках и диаграммах
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.9 Как решать сложные пропорции с неизвестными?
- 1.10 Виды задач на пропорции и их решение
Узнайте, как решать пропорцию в математике с помощью подробных объяснений и примеров. Научитесь применять правила пропорциональности для нахождения неизвестных значений в уравнениях пропорции.
Пропорции являются важным инструментом в математике, который позволяет сравнивать и находить соотношения между различными величинами. Как правило, пропорции используются для решения задач, связанных с пропорциональными отношениями и подобием объектов. В этой статье мы подробно рассмотрим, как решать пропорции и приведем несколько примеров для лучшего понимания.
Для начала, давайте определим, что такое пропорция. Пропорция — это уравнение, устанавливающее равенство двух отношений. Пропорция обычно записывается в виде a/b = c/d, где a, b, c и d — это числа. Важно отметить, что пропорция остается равной даже при изменении чисел a, b, c и d в одно и то же число раз.
Как решать пропорции? Существует несколько способов. Один из самых простых способов — использование крест-мультипликации. Прежде всего, необходимо умножить числа a и d и затем умножить числа b и c. Затем полученные произведения сравниваются между собой. Если они равны, то пропорция сбалансирована и числа a, b, c и d пропорциональны. Если произведения разные, значит, пропорция не сбалансирована и числа не пропорциональны.
Пример: Если имеется пропорция 2/3 = x/6, чтобы найти значение x, нужно умножить числа 2 и 6, а затем разделить произведение на число 3 (2*6/3). Таким образом, x = 4.
Решение пропорций может быть полезно во многих областях науки и повседневной жизни. Например, пропорциональные отношения используются при расчете смесей, дозировке лекарств, строительстве, финансовых расчетах и даже при создании искусства. Понимание и умение решать пропорции помогут вам в решении разнообразных задач и повысят вашу математическую грамотность.
Что такое пропорции в математике?
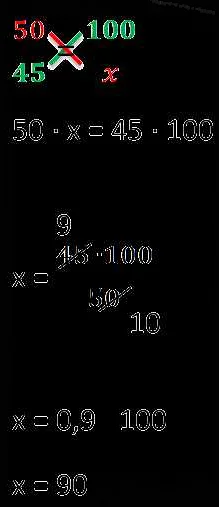
Пропорции имеют вид a:b = c:d, где a, b, c, d – числа, называемые частями пропорции. Чтобы определить, являются ли эти числа пропорциональными, необходимо проверить, равны ли их отношения.
Пропорции могут быть использованы для решения различных задач, таких как нахождение неизвестного числа в пропорции, сравнение величин и нахождение пропорциональных значений.
Пропорции широко применяются в различных областях математики и реальной жизни, таких как финансы, геометрия, физика и экономика. Например, пропорции используются для расчета скидок и наценок, определения соотношения сторон в геометрических фигурах и анализа зависимостей между различными величинами.
Основные понятия и определения
Пропорциональность — это свойство, при котором две пропорции имеют одинаковые значения. Если изменить числитель или знаменатель одного отношения, то и другие отношения также изменятся пропорционально.
Пропорциональные отношения — это отношения, в которых изменение одного величины приводит к пропорциональному изменению другой величины. В пропорциональных отношениях отношение между числителями равно отношению между знаменателями.
Решение пропорции — это процесс нахождения неизвестной величины в пропорции, используя известные отношения и свойства пропорциональности.
Примеры пропорций:
- 3:5 = 6:10
- 2:4 = 1:2
- 8:12 = 2:3
Как решать пропорции с помощью кросс-метода?
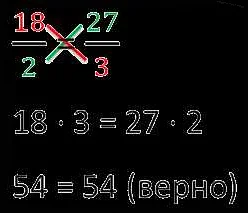
Для решения пропорций с помощью кросс-метода необходимо выполнить следующие шаги:
- Запишите пропорцию в виде двух дробей, где числитель первой дроби соответствует числителю второй дроби, а знаменатель первой дроби соответствует знаменателю второй дроби.
- Обозначьте неизвестное значение, которое нужно найти, переменной x.
- Умножьте числитель первой дроби на знаменатель второй дроби и присвойте результат переменной a.
- Умножьте числитель второй дроби на знаменатель первой дроби и присвойте результат переменной b.
- Установите равенство a = b и решите полученное уравнение относительно переменной x.
- Подставьте найденное значение x в пропорцию и проверьте его.
Пример решения пропорции с помощью кросс-метода:
Дана пропорция: 4/6 = x/9
Шаги решения:
- Запишем пропорцию в виде двух дробей: 4/6 = x/9
- Обозначим неизвестное значение x.
- Умножим числитель первой дроби на знаменатель второй дроби: 4 * 9 = 36. Присвоим результат переменной a.
- Умножим числитель второй дроби на знаменатель первой дроби: 6 * x = 6x. Присвоим результат переменной b.
- Установим равенство a = b: 36 = 6x.
- Решим полученное уравнение относительно x: 6x = 36, x = 36 / 6, x = 6.
- Подставим найденное значение x в пропорцию: 4/6 = 6/9. Видим, что пропорция выполняется.
Таким образом, мы решили пропорцию 4/6 = x/9 с помощью кросс-метода и получили значение x = 6.
Примеры решения пропорций
Ниже приведены несколько примеров решения пропорций, чтобы дать вам представление о том, как это делается.
- Пример 1:
Решим пропорцию:
2/3 = x/6
Перекрестно умножаем:
2 * 6 = 3 * x
Решаем полученное уравнение:
12 = 3x
Делим обе части уравнения на 3:
x = 4
Таким образом, x = 4 является решением пропорции.
- Пример 2:
Решим пропорцию:
5/8 = 15/y
Перекрестно умножаем:
5 * y = 8 * 15
Решаем полученное уравнение:
5y = 120
Делим обе части уравнения на 5:
y = 24
Таким образом, y = 24 является решением пропорции.
- Пример 3:
Решим пропорцию:
3/4 = 12/z
Перекрестно умножаем:
3 * z = 4 * 12
Решаем полученное уравнение:
3z = 48
Делим обе части уравнения на 3:
z = 16
Таким образом, z = 16 является решением пропорции.
Надеюсь, эти примеры помогут вам лучше понять, как решать пропорции. Практикуйтесь, и скоро вы станете мастером в решении пропорций!
Как использовать пропорции в реальной жизни?
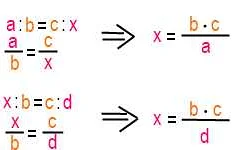
1. Смешивание ингредиентов в кулинарии: Когда мы готовим, нам часто нужно смешивать ингредиенты в определенных пропорциях. Например, рецепт может требовать, чтобы мы смешали 2 столовые ложки сахара и 1 столовую ложку муки. В этом случае мы можем использовать пропорцию, чтобы определить, сколько ингредиентов нам нужно, если мы хотим приготовить больше или меньше порций.
2. Расчет времени и расстояния: Пропорции можно использовать для определения времени, которое займет путешествие на определенном расстоянии. Например, если мы знаем, что мы едем со скоростью 60 км/ч и нам нужно проехать 300 км, мы можем использовать пропорцию, чтобы найти время, которое мы потратим на путешествие.
3. Расчет финансовых показателей: Пропорции могут быть полезны при расчете финансовых показателей, таких как проценты, налоги и скидки. Например, если мы хотим узнать, сколько мы сэкономим на покупке со скидкой 20%, мы можем использовать пропорцию для расчета суммы скидки.
4. Увеличение и уменьшение масштаба: Пропорции также могут быть применены для увеличения или уменьшения масштаба объектов или изображений. Например, архитекторы используют пропорции, чтобы создать масштабные модели зданий.
Это только несколько примеров того, как мы можем использовать пропорции в реальной жизни. Они помогают нам решать различные задачи и делают нашу жизнь более удобной и предсказуемой.
Пропорции в графиках и диаграммах
Пропорции играют важную роль в создании и интерпретации графиков и диаграмм. Правильное использование пропорций позволяет наглядно отобразить данные и делает информацию более понятной и доступной.
В графиках, пропорции могут использоваться для отображения отношений между различными элементами. Например, на круговой диаграмме пропорции могут показывать, какую часть всей суммы составляет каждый элемент. Большой сектор будет соответствовать большей доле, а маленький — меньшей.
В столбчатых и линейных графиках, пропорции могут отображать различные значения или изменения величин на оси x и y. На оси x можно отобразить различные категории или периоды времени, а на оси y — соответствующие значения или процентное отношение.
Важно также уметь правильно масштабировать графики, чтобы сохранить соотношение между значениями. Неправильное масштабирование может исказить пропорции и привести к неправильному искажению данных.
При создании или интерпретации графиков и диаграмм, необходимо учитывать пропорции и стараться представить данные четко и точно. Это помогает создавать наглядные и информативные графические представления, которые помогают лучше понять и проанализировать данные.
Видео по теме:
Вопрос-ответ:
Как решать пропорции в математике?
Для решения пропорций в математике следует использовать правило трех, при котором все четыре числа в пропорции делятся на одно общее число. Затем, применяя правило трех, можно найти значение неизвестного числа в пропорции.
Можете привести пример решения пропорции?
Конечно! Решим пропорцию: 3/5 = x/10. Сначала умножаем числа на косвенные пропорции: 5 * x = 3 * 10. Затем решаем полученное уравнение: 5x = 30. И, наконец, делим обе стороны на 5: x = 6. Таким образом, значение неизвестного числа x равно 6.
Каким образом можно проверить правильность решения пропорции?
Для проверки правильности решения пропорции можно подставить найденное значение неизвестного числа в исходную пропорцию и убедиться, что обе стороны равны. Если это так, то решение верное.
Я не очень хорошо понимаю, что такое пропорция. Можете объяснить?
Конечно! Пропорция — это математическое соотношение между двумя или более значениями. В пропорции есть две пары чисел, где каждая пара состоит из числа и его коэффициента. Важно, чтобы отношение между числами в одной паре было равно отношению чисел в другой паре.
Какие еще способы есть для решения пропорции?
Помимо правила трех, существуют и другие способы для решения пропорций, такие как использование косвенных пропорций или применение обратного отношения. В зависимости от задачи, можно выбрать наиболее подходящий способ для решения пропорции.
Как решать сложные пропорции с неизвестными?

Решение сложных пропорций с неизвестными требует некоторого усилия и внимания. Вам понадобится использовать навыки пропорционального рассуждения и алгебры для определения значения неизвестных в заданной пропорции.
Шаги для решения сложных пропорций с неизвестными:
- Изучите заданную пропорцию и определите, какие значения известны, а какие нужно найти.
- Упростите пропорцию, если это возможно, сократив общие множители.
- Используйте свойства пропорций, чтобы выразить неизвестные величины в виде уравнений.
- Решите полученные уравнения, используя алгебру. Выразите неизвестные величины через известные и найдите их значения.
- Проверьте полученные значения, подставив их обратно в исходную пропорцию. Убедитесь, что оба равенства выполняются.
Пример решения сложной пропорции с неизвестными:
Дана пропорция: 3/x = 5/15. Нам нужно найти значение x.
Сначала упростим пропорцию, сократив общие множители: 1/x = 1/3.
Затем используем свойства пропорций для выражения неизвестной величины x в виде уравнения: 1 = x/3.
Решим полученное уравнение, умножив обе стороны на 3: 3 = x.
Таким образом, значение x равно 3.
Проверим полученное значение, подставив его обратно в исходную пропорцию: 3/3 = 5/15. Оба равенства выполняются, что означает, что наше решение верно.
Таким образом, мы успешно решили сложную пропорцию с неизвестными и нашли значение x.
Виды задач на пропорции и их решение
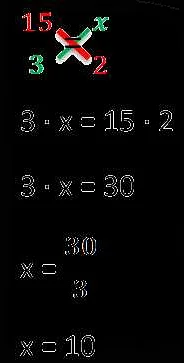
Пропорции широко применяются в математике для решения различных задач. Вот несколько видов задач, где пропорции играют важную роль:
1. Задачи на распределение величин.
В таких задачах известны несколько величин, и требуется распределить их пропорционально некоторому условию. Например, задача может состоять в распределении суммы денег между несколькими людьми в зависимости от их достатка.
2. Задачи на смешивание веществ.
Если несколько веществ различной концентрации смешиваются, то можно использовать пропорции для определения конечной концентрации или объема смеси. Это часто применяется в химии при разведении растворов или смешивании различных жидкостей.
3. Задачи на подобие.
Подобие – это свойство геометрических фигур, когда они имеют одинаковую форму, но разные размеры. В задачах на подобие можно использовать пропорции для определения соотношения длин сторон или площадей подобных фигур.
Как решать задачи на пропорции?
Для решения задач на пропорции следуйте следующим шагам:
- Составьте пропорцию, связывающую известные величины.
- Используйте свойство равенства частей пропорции для нахождения неизвестных величин.
- Решите полученное уравнение, чтобы найти значения неизвестных величин.
- Проверьте полученные значения, подставив их в исходную пропорцию.
Важно помнить, что в задачах на пропорции необходимо сохранять единицы измерения и учитывать контекст задачи при интерпретации результатов.
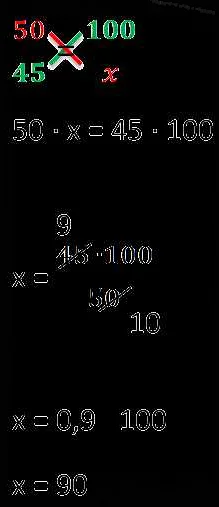

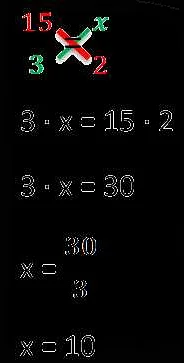


Статья очень понравилась! Я долго искал информацию о том, как решать пропорции в математике, и ваше подробное объяснение дало мне все необходимые инструменты. Я теперь полностью понимаю, как применять правило трех и как использовать крестовое правило для решения пропорций. Ваши примеры очень наглядны и помогли мне закрепить полученные знания. Теперь я больше не боюсь сложных пропорциональных задач, и уверен, что смогу решить их без проблем. Спасибо за такую полезную статью!