Что значит составное число в математике

Составное число — это натуральное число, которое имеет более двух делителей. В математике они играют важную роль и используются в различных арифметических операциях и задачах.

Составное число — это натуральное число, которое имеет больше двух делителей. Другими словами, это число, которое можно разделить на более чем два натуральных числа без остатка. Например, число 6 является составным, так как его можно разделить на 1, 2, 3 и 6. Однако, число 5 является простым числом, так как оно имеет только два делителя — 1 и 5.

Составные числа обладают множеством интересных свойств и являются важным понятием в теории чисел. Они могут быть представлены в виде произведения простых чисел, что называется факторизацией. Например, число 12 можно представить в виде произведения 2 * 2 * 3. Такое представление помогает анализировать и работать с составными числами.

Изучение составных чисел имеет важное практическое значение, особенно в криптографии и факторизации больших чисел. Например, в алгоритме RSA составные числа используются для защиты информации, а факторизация больших чисел служит основой для сложных шифровальных систем.

Знание о составных числах помогает понять многие математические концепции и является фундаментом для дальнейшего изучения математики. Поэтому, понимание определения и примеров составных чисел является важной задачей для любого учащегося.

Определение составного числа

Например, число 12 является составным, потому что его можно разложить на множители 2 и 6, или 3 и 4. В отличие от составных чисел, простые числа имеют только два делителя — 1 и само число.

Существует бесконечное количество составных чисел. Они играют важную роль в теории чисел и используются в различных математических алгоритмах и задачах.

Для определения, является ли число составным, можно использовать различные методы, такие как проверка делителей числа или использование алгоритма факторизации.

Таблица ниже показывает некоторые примеры составных чисел:

ЧислоМножители

4	2, 2
6	2, 3
9	3, 3
15	3, 5

Признаки составного числа

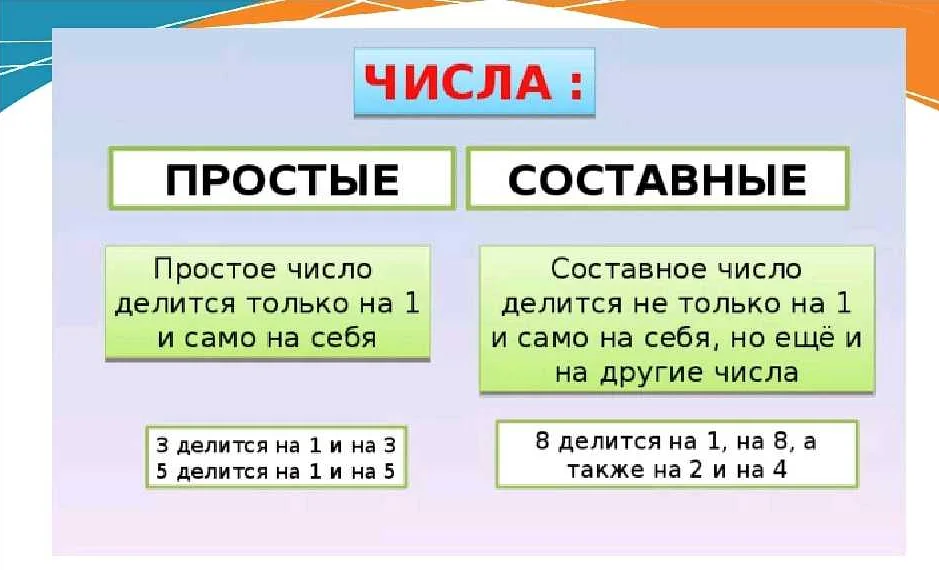
Основные признаки составного числа:

1.	Составное число всегда делится на единицу и на само себя без остатка.
2.	У составного числа есть делители, отличные от единицы и самого числа.
3.	Если число является квадратом некоторого натурального числа, то оно обязательно является составным.
4.	Если число оканчивается на 0, 2, 4, 6, или 8, то оно обязательно является составным.
5.	Если число делится на 2 или 5, то оно также является составным.

Например, число 12 является составным числом, так как оно делится на 1, 2, 3, 4, 6 и 12. В то же время, число 7 является простым числом, так как оно делится только на 1 и на себя.

Простые числа и составные числа

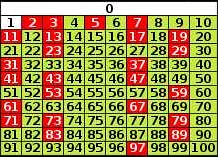
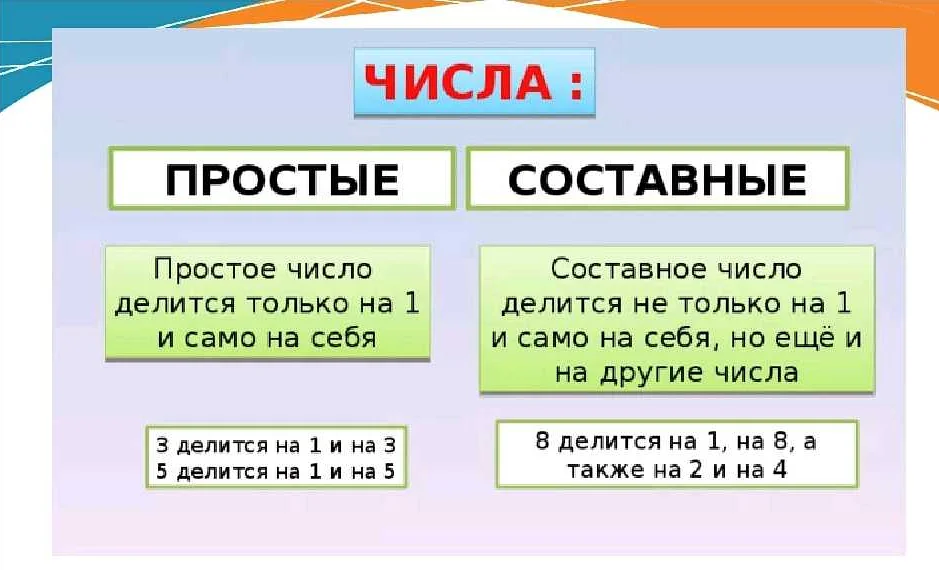
В математике числа делятся на две основные категории: простые числа и составные числа.

Простые числа — это числа, которые имеют только два делителя: 1 и само число. Например, числа 2, 3, 5, 7 и 11 являются простыми числами.

Составные числа — это числа, которые имеют больше двух делителей. Они могут быть разложены на множители, отличные от 1 и самого числа. Например, число 4 является составным числом, так как оно может быть разложено на множители 2 * 2.

Простые числа обладают рядом интересных свойств и играют важную роль в теории чисел. Они являются основным строительным блоком для составных чисел, так как любое составное число может быть разложено на простые множители.

Например, число 12 является составным числом, так как оно может быть разложено на множители 2 * 2 * 3. В этом примере, числа 2 и 3 являются простыми множителями.

Знание о простых и составных числах является важным для решения множества задач в математике и других областях. Оно позволяет анализировать и работать с числами, а также применять их в различных алгоритмах и шифрах.

Разложение составного числа на простые множители

Процесс разложения составного числа на простые множители начинается с поиска его наименьшего простого делителя. Затем найденный простой делитель делит составное число, и полученный результат снова разлагается на простые множители. Этот процесс продолжается до тех пор, пока не будут разложены все множители составного числа.

Например, рассмотрим число 24. Его наименьшим простым делителем является число 2. Поделим число 24 на 2 и получим 12. Затем разложим число 12 на простые множители – 2 и 6. Продолжая процесс, разложим число 6 на простые множители – 2 и 3. Таким образом, число 24 разлагается на простые множители 2 * 2 * 2 * 3.

Разложение составного числа на простые множители позволяет нам более удобно и компактно представить данное число, а также позволяет проводить дальнейшие математические операции с ним.

Примеры составных чисел

Составным числом называется любое натуральное число, которое больше единицы и имеет делители, отличные от единицы и самого числа. Вот несколько примеров составных чисел:

1. 4 — это составное число, так как оно делится на 2 и 4.
2. 6 — это составное число, так как оно делится на 2, 3 и 6.
3. 8 — это составное число, так как оно делится на 2, 4 и 8.
4. 9 — это составное число, так как оно делится на 3 и 9.
5. 10 — это составное число, так как оно делится на 2, 5 и 10.

Это лишь некоторые примеры составных чисел. В математике существует бесконечное количество составных чисел, и их можно найти путем деления числа на все возможные делители и проверки, есть ли делители, отличные от единицы и самого числа.

Тест на простоту числа

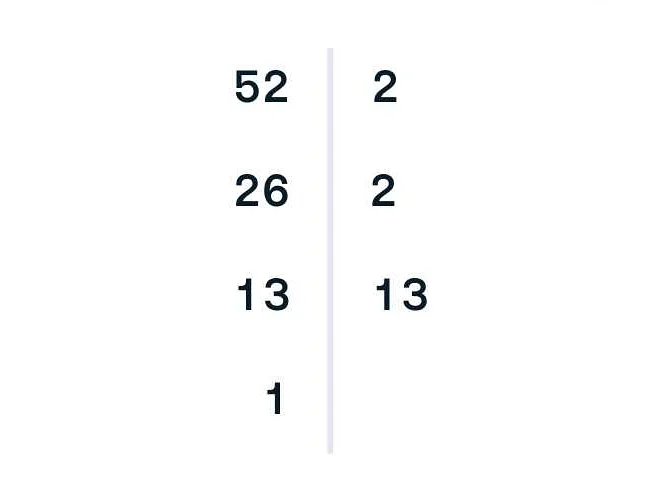
Существует несколько алгоритмов для тестирования чисел на простоту. Один из самых простых и распространенных алгоритмов – это перебор делителей числа. Для этого мы идем от двух до корня из числа и проверяем, делится ли исходное число на каждое из этих чисел без остатка. Если число делится хотя бы на одно из них, то оно является составным. В противном случае, если число не делится ни на одно из этих чисел, то оно является простым.

Например, чтобы проверить, является ли число 17 простым, мы проверим делится ли оно на числа 2, 3, 4, …, 16. Если мы не найдем ни одного делителя, то число 17 будет простым.

Тест на простоту числа является важным инструментом в различных областях математики и криптографии. Он используется в алгоритмах шифрования, генерации случайных чисел и других задачах, где безопасность и надежность чисел играют важную роль.

Применение составных чисел в криптографии

Составные числа играют важную роль в криптографии, науке, изучающей методы защиты информации. Они используются для создания криптографических алгоритмов, а именно алгоритма RSA (Rivest-Shamir-Adleman).

Алгоритм RSA основан на том, что разложение большого составного числа на простые множители является трудоемкой задачей, особенно при использовании больших чисел. Это свойство делает его надежным для использования в криптографии.

Процесс генерации ключей для алгоритма RSA включает выбор двух различных простых чисел и их перемножение, получая составное число. Затем происходит поиск такого числа, которое является взаимно простым с заданным составным числом. Это число и будет использоваться в качестве открытого ключа, а само составное число будет использоваться в качестве закрытого ключа.

Криптографические алгоритмы, основанные на использовании составных чисел, обеспечивают высокую степень безопасности при передаче и хранении информации. Это происходит благодаря трудоемкости разложения составного числа на простые множители и возможности использования двух различных ключей для шифрования и дешифрования данных.

Таким образом, составные числа играют важную роль в криптографии, обеспечивая надежную защиту информации от несанкционированного доступа.

Вопрос-ответ:

Что такое составное число?

Составное число — это натуральное число, которое имеет более двух делителей. Иными словами, это число, которое можно разделить на другие числа, кроме 1 и самого себя.

Как можно определить, является ли число составным?

Чтобы определить, является ли число составным, нужно проверить, есть ли у него делители, отличные от 1 и самого числа. Если такие делители есть, то число является составным. Если же нет, то число является простым.

Какие примеры можно привести составных чисел?

Некоторыми примерами составных чисел являются: 4, 6, 8, 9, 10 и так далее. Эти числа могут быть разделены на более чем два делителя.

Какое число не является составным?

Число 1 не является составным числом, так как оно имеет только один делитель — само себя. Остальные натуральные числа могут быть как составными, так и простыми.

Видео по теме: