Что такое сравнение математика
Содержимое
- 1 Что такое сравнение математика
- 1.1 Сравнение математика: понятие, примеры и правила
- 1.2 Определение и основные понятия
- 1.3 Примеры сравнений в математике
- 1.4 Правила сравнения чисел и выражений
- 1.5 Сравнение натуральных чисел
- 1.6 Сравнение целых чисел
- 1.7 Сравнение десятичных дробей
- 1.8 Сравнение дробей с разными знаменателями
- 1.9 Сравнение процентов и десятичных дробей
- 1.10 Видео по теме:
Сравнение в математике — это процесс определения отношения между двумя или более числами, объектами или явлениями, чтобы узнать, одинаковы они или различны. Сравнение может осуществляться по различным критериям, таким как равенство, больше/меньше, пропорциональность и т. д. Понимание сравнения в математике является важным элементом развития логического мышления и аналитических навыков.
Сравнение — одна из основных операций в математике, которая позволяет определить отношение между двумя числами или выражениями. Оно помогает сравнить их величину и определить, какое из них больше, меньше или равно другому.
Для выполнения сравнения используются специальные математические символы. Например, знак «меньше» () и знак «равно» (=). Но сравнение может быть не только строгим, но и неравным, когда одно число больше или меньше другого, но не равно ему.
Например, выражение 5 > 3 говорит о том, что число 5 больше числа 3. А выражение 4 < 7 означает, что число 4 меньше числа 7.
Сравнение в математике имеет свои правила. Например, если к двум числам применяется одинаковая операция (сложение, вычитание, умножение или деление), то результат сравнения будет таким же, как результат операции.
Например, если 2 + 3 = 5 и 4 + 1 = 5, то 2 + 3 = 4 + 1.
Сравнение математика: понятие, примеры и правила

Примеры сравнения включают сравнение чисел, элементов векторов, множеств, углов и других математических объектов. Например, можно сравнить два числа, чтобы определить, какое из них больше или меньше.
Сравнение в математике следует определенным правилам. Для сравнения чисел используются математические операторы: больше (>), меньше ( 3 означает, что число 5 больше числа 3.
Сравнение объектов также может быть основано на их свойствах. Например, можно сравнить два вектора по их длине или два множества по количеству элементов.
Основное правило сравнения состоит в том, что сравнение должно быть симметричным. То есть, если A > B, то B < A. Если A = B, то B = A. Если A ≤ B и B ≤ A, то A = B.
Сравнение математика имеет широкое применение в различных областях, включая алгебру, геометрию, теорию вероятностей и другие.
Определение и основные понятия

Операторы сравнения используются для сравнения значений и возвращают логическое значение — истина или ложь. Результат сравнения может быть записан в виде логического выражения или использован в условных выражениях.
Основными операторами сравнения являются:
- Больше (>), меньше ( — эти операторы сравнивают два числа и возвращают истину, если первое число больше (меньше) второго.
- Больше или равно (>=), меньше или равно ( — эти операторы сравнивают два числа и возвращают истину, если первое число больше или равно (меньше или равно) второму.
- Равно (==) — этот оператор сравнивает два числа и возвращает истину, если они равны.
- Не равно (!=) — этот оператор сравнивает два числа и возвращает истину, если они не равны.
При сравнении целых чисел применяются также понятия положительного и отрицательного числа. Положительное число больше нуля, отрицательное число меньше нуля.
Сравнение в математике является основой для работы с числами и позволяет установить их отношение друг к другу.
Примеры сравнений в математике
В математике существуют следующие символы сравнения:
- Меньше (<): указывает, что число или выражение слева от символа меньше числа или выражения справа.
- Больше (>): указывает, что число или выражение слева от символа больше числа или выражения справа.
- Меньше или равно (≤): указывает, что число или выражение слева от символа меньше или равно числу или выражению справа.
- Больше или равно (≥): указывает, что число или выражение слева от символа больше или равно числу или выражению справа.
- Равно (=): указывает, что число или выражение слева от символа равно числу или выражению справа.
- Не равно (≠): указывает, что число или выражение слева от символа не равно числу или выражению справа.
Примеры сравнений:
1. 5 < 10 (пять меньше десяти)
2. 15 > 7 (пятнадцать больше семи)
3. 4 ≤ 4 (четыре меньше или равно четырем)
4. 9 ≥ 3 (девять больше или равно трем)
5. 6 = 6 (шесть равно шести)
6. 12 ≠ 8 (двенадцать не равно восьми)
Символы сравнения позволяют установить отношение между числами или выражениями и являются важным инструментом в математике для сравнения и анализа различных величин.
Правила сравнения чисел и выражений
Правила сравнения чисел:
- Для сравнения двух чисел используется знак сравнения: больше (>), меньше (
- Если одно число больше другого, то оно располагается справа от знака сравнения.
- Если одно число меньше другого, то оно располагается слева от знака сравнения.
- Если два числа равны, то они располагаются по обе стороны от знака равенства (=).
Правила сравнения выражений:
- Сравнение выражений выполняется по аналогии с сравнением чисел.
- Если выражение состоит из нескольких частей, то оно сравнивается покомпонентно, начиная с самой левой части.
- Если выражение содержит операции сложения и вычитания, то при сравнении имеет место приоритетность этих операций.
- Если выражение содержит операции умножения и деления, то при сравнении имеет место приоритетность этих операций.
Правила сравнения чисел и выражений являются основой для решения различных задач и уравнений в математике. Их усвоение позволяет проводить сравнение и анализ числовых данных с большей точностью и эффективностью.
Сравнение натуральных чисел
1. Числа равны: два числа считаются равными, если они имеют одинаковое количество единиц.
2. Число больше: число A считается больше числа B, если в числе A есть цифры, которых нет в числе B.
3. Число меньше: число A считается меньше числа B, если в числе B есть цифры, которых нет в числе A.
Например, для чисел 123 и 456 выполнение сравнения будет следующим:
Число 123 меньше числа 456, так как в числе 456 есть цифры 4 и 5, которых нет в числе 123.
Сравнение натуральных чисел имеет важное значение при решении различных математических задач и задач из повседневной жизни. Оно позволяет установить отношение между числами и определить их порядок.
Сравнение целых чисел

Правила сравнения целых чисел:
- Если два числа имеют одинаковые знаки (положительный или отрицательный), то большим считается число с большим модулем, то есть по абсолютной величине.
- Если два числа имеют разные знаки (одно положительное, другое отрицательное), то положительное число всегда больше отрицательного числа.
- Если два числа равны по абсолютной величине, но имеют разные знаки, то считается, что отрицательное число меньше положительного.
Например, сравним числа -5 и -3:
- -5 больше -3, так как у обоих чисел отрицательный знак, но -5 имеет больший модуль.
А теперь сравним числа 7 и -2:
- 7 больше -2, так как у чисел разные знаки, и положительное число всегда больше отрицательного.
Таким образом, сравнение целых чисел позволяет определить их относительное положение друг относительно друга.
Сравнение десятичных дробей
Для сравнения десятичных дробей необходимо сравнить их целые части. Если целые части равны, то следует сравнить дробные части. Для этого нужно сравнить цифры после запятой: начиная с первой цифры слева и двигаясь вправо.
При сравнении десятичных дробей можно использовать следующие правила:
- Если целая часть одной десятичной дроби больше целой части другой, то она считается больше.
- Если целые части равны, то сравниваются дробные части. Если первая различная цифра в дробной части первой дроби больше соответствующей цифры второй дроби, то первая дробь считается больше.
- Если целые и дробные части двух десятичных дробей равны, то они считаются равными.
Например, чтобы сравнить десятичные дроби 0.25 и 0.5, нужно сравнить их целые части, которые равны нулю. Затем следует сравнить дробные части: первая различная цифра в дробной части 0.25 это 2, а в дробной части 0.5 это 5. Таким образом, 0.5 больше 0.25.
Сравнение десятичных дробей является важной математической операцией, которая позволяет определить отношение между числами и использовать их в различных математических задачах и вычислениях.
Сравнение дробей с разными знаменателями
Для сравнения дробей с разными знаменателями необходимо привести их к общему знаменателю. Для этого нужно найти наименьшее общее кратное (НОК) знаменателей двух дробей. НОК можно найти путем разложения знаменателей на простые множители и выбора наибольшей степени каждого простого числа.
После приведения дробей к общему знаменателю можно сравнивать их числители. Если числитель одной дроби больше числителя другой, то первая дробь больше. Если числители равны, то сравнивают знаки дробей: если оба числителя положительны или оба отрицательны, то дроби равны, если один из числителей отрицателен, а другой положителен, то дробь с положительным числителем больше.
Например, рассмотрим дроби 1/4 и 2/3. Найдем их общий знаменатель: знаменатель 4 можно представить в виде 2^2, а знаменатель 3 — в виде 3^1. Тогда НОК равно 2^2 * 3^1 = 12. Приведем дроби к общему знаменателю: 1/4 = 3/12, 2/3 = 8/12. После этого сравним числители: 3 < 8, поэтому 1/4 < 2/3.
Таким образом, сравнение дробей с разными знаменателями требует приведения к общему знаменателю и сравнения числителей после этого преобразования.
Сравнение процентов и десятичных дробей
Проценты представляют собой доли от целого, которые выражены в сотых долях. Например, 50% равно половине, а 75% равно трём четвертым. Десятичные дроби, с другой стороны, представляют себе доли от целого, которые выражены в десятичной системе счисления. Например, 0,5 равно половине, а 0,75 равно трём четвертым.
Для сравнения процентов и десятичных дробей необходимо привести их к одной и той же форме. Например, можно привести проценты к десятичной форме, умножив их на 0,01. Таким образом, 50% будет равно 0,5, а 75% будет равно 0,75. После этого можно сравнить эти десятичные числа.
Правила сравнения процентов и десятичных дробей аналогичны правилам сравнения обычных чисел. Если десятичная дробь или процент больше другой, то она является большей. Например, если 0,5 больше 0,25, то 50% больше 25%. Если десятичные дроби или проценты равны, то они являются равными.
Важно помнить, что сравнение процентов и десятичных дробей может быть полезным при решении различных задач, особенно связанных с финансовой математикой. Например, при сравнении процентных ставок по вкладам или кредитам, а также при анализе изменения цен на товары или услуги.
Видео по теме:
Что такое сравнение в математике?
Сравнение в математике — это операция, при помощи которой сравниваются два или более числа или выражения, чтобы определить, которое из них больше, меньше или равно другому.
Что такое сравнение математика?
Сравнение в математике — это процесс сопоставления двух или более чисел для определения, какое из них больше, меньше или равно другому числу.


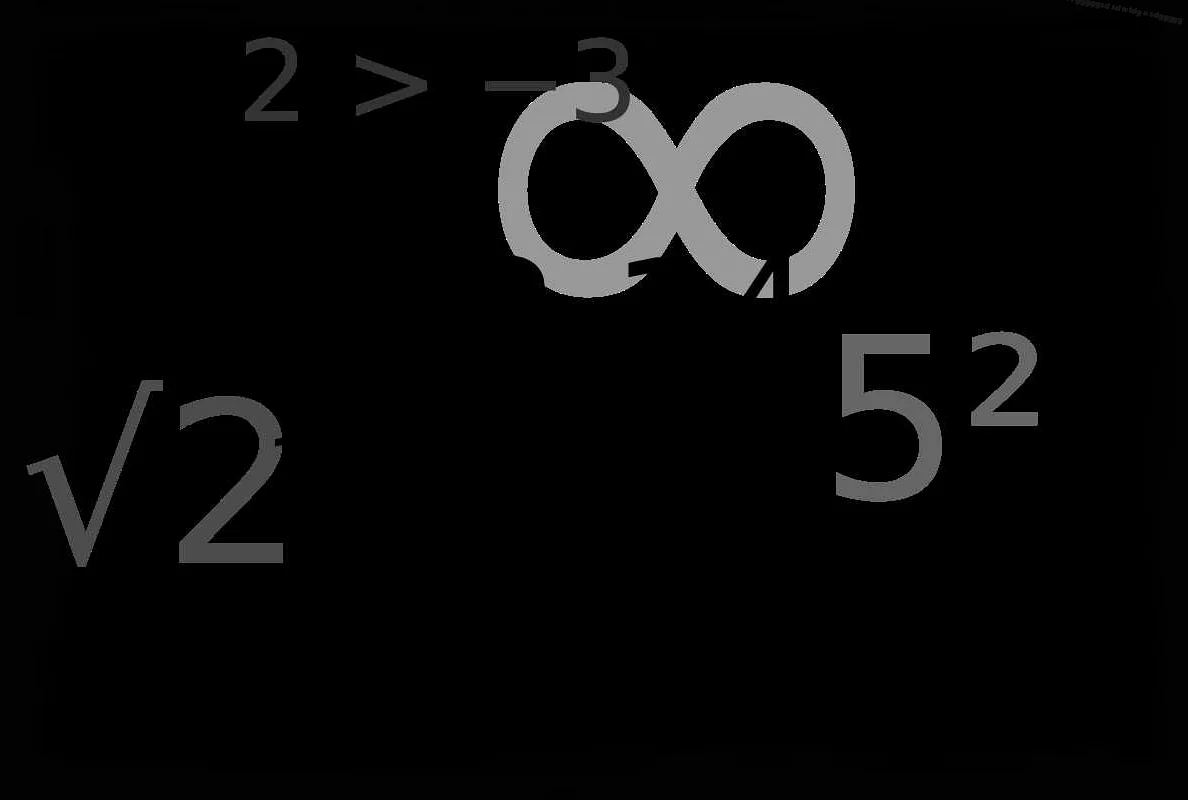

Статья очень понятно и подробно объясняет, что такое сравнение в математике. Я, как обычный читатель, ранее слышал о сравнении, но не всегда понимал его смысл. Автор статьи привел примеры, которые помогли мне лучше понять, как используется сравнение в математике. Особенно мне понравилось, как автор объяснил правила сравнения и как их применять. Теперь я чувствую, что получил хорошую основу для дальнейшего изучения математики. Большое спасибо автору за информативную и доступную статью!