Что называется степенью в математике
Содержимое
- 1 Что называется степенью в математике
Степень в математике — это операция, позволяющая возвести число в некоторую степень. Степень может быть целой, дробной или отрицательной. В данной статье рассмотрены основные понятия и свойства степени, а также приведены примеры вычислений степеней.
Степень — это одно из основных понятий в математике, которое используется для выражения множества операций и отношений. В математическом понимании степень означает повторное умножение числа на себя. В степенной записи число, которое нужно умножить на себя несколько раз, называется основанием, а количество повторений — показателем степени.
Определение степени
Степень числа выражается в виде основания, записанного в верхнем индексе, и показателя степени, записанного внизу. Например, в выражении 23 основание равно 2, а показатель степени равен 3. Это можно прочитать как «2 в степени 3» или «2 в кубе».
Примеры степени
1. 42 = 4 * 4 = 16
2. 53 = 5 * 5 * 5 = 125
3. 100 = 1
Степени широко используются в различных областях математики, физики, экономики и других науках. Они позволяют удобно записывать и вычислять очень большие и очень маленькие числа, а также описывать законы и зависимости в природе и обществе.
Что такое степень в математике
Степень обозначается с помощью верхнего индекса, который показывает число повторений умножения.
Например, если число 3 возвести в степень 2, то получим 3^2, что равно 3 * 3 = 9.
В математике также существуют особые степени, такие как нулевая степень и отрицательная степень.
- Нулевая степень: a^0 = 1. Независимо от значения числа a, его нулевая степень будет равна 1.
- Отрицательная степень: a^(-n) = 1/(a^n). Число a в отрицательной степени равно единице, деленной на значение числа a в положительной степени.
Степени широко используются в математике для упрощения и обозначения множества операций, а также для решения сложных задач и формулировки законов.
Видео по теме:
Определение степени
Степень числа представляется в виде двух чисел: основания и показателя степени.
Основание степени — это число, которое нужно возвести в степень.
Показатель степени — это число, указывающее, сколько раз основание должно быть умножено на себя.
Степень обозначается с помощью знака «^».
Например, степень числа 2 второй степени (2^2) равна 2 умножить на 2, что равно 4.
Степень может быть положительной, отрицательной или нулевой.
При положительной степени основание умножается на себя столько раз, сколько указано в показателе степени.
При отрицательной степени основание берется за знаменатель дроби с единичным числителем и показателем степени по модулю.
При нулевой степени любое число, кроме нуля, возводится в нулевую степень и равно 1.
Примеры степени
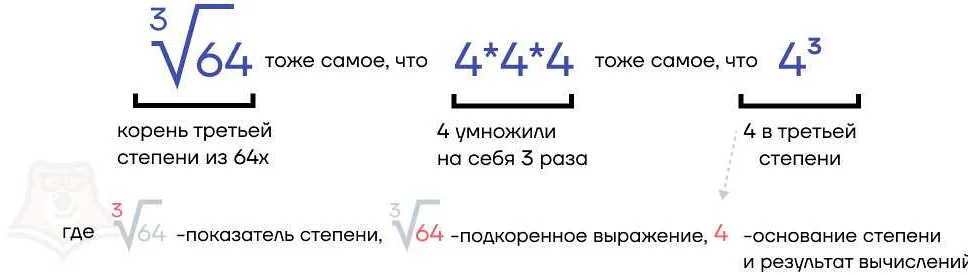
Примеры степени:
- 23 = 2 * 2 * 2 = 8
- 52 = 5 * 5 = 25
- 100 = 1
В первом примере число 2 возводится в степень 3, что равносильно умножению 2 на само себя 3 раза: 2 * 2 * 2 = 8.
Во втором примере число 5 возводится в степень 2, что равносильно умножению 5 на само себя: 5 * 5 = 25.
В третьем примере число 10 возводится в степень 0, что равно единице: 100 = 1.
Вопрос-ответ:
Что такое степень в математике?
Степень в математике — это операция, которая позволяет возвести число в некоторую степень. В результате получается новое число, которое получается путем многократного перемножения данного числа на себя.
Как записывается степень в математике?
Степень в математике записывается с помощью знака «^». Например, 2^3 означает, что число 2 нужно возвести в степень 3, то есть перемножить его на себя 3 раза.
Какие есть основные правила работы со степенями?
Основные правила работы со степенями включают правила умножения степеней с одинаковыми основаниями, правила деления степеней с одинаковыми основаниями, а также правила возведения в степень степени.
Как вычислить степень числа?
Для вычисления степени числа нужно перемножить это число само на себя столько раз, сколько указано в степени. Например, для вычисления 2^3 нужно умножить число 2 на себя 3 раза: 2 * 2 * 2 = 8.
Какие есть примеры степеней в математике?
Примеры степеней в математике включают 2^3, что равно 2 * 2 * 2 = 8, а также 5^2, что равно 5 * 5 = 25. В обоих случаях число возводится в указанную степень путем многократного перемножения на себя.
Степень числа

Степень числа обозначается с помощью верхнего индекса. Например, число 3 в кубе обозначается как 3³, где число 3 — основание степени, а число 3 — показатель степени.
Если показатель степени равен 0, то любое число, кроме 0, возведенное в степень 0, равно 1. Например, 5⁰ = 1.
Если показатель степени положителен, то число возводится в степень, как указано. Например, 2² = 2 × 2 = 4.
Если показатель степени отрицателен, то число возводится в степень, а затем обратное значение полученного числа берется. Например, 2⁻² = 1 / (2 × 2) = 1 / 4 = 0.25.
Возведение числа в степень является одной из основных операций в алгебре и имеет широкое применение в различных областях, включая физику, экономику и программирование.
Показатель степени
Обозначается показатель степени в верхнем правом углу основания степени. Например, если мы имеем выражение 23, то число 3 является показателем степени.
Показатель степени может быть любым целым числом, в том числе и отрицательным. Если показатель степени положительный, то получается положительное число. Если показатель степени отрицательный, то получается дробное число или число с отрицательным показателем степени.
Примеры:
1. 23 = 2 * 2 * 2 = 8. Здесь показатель степени равен 3.
2. 50 = 1. Любое число, возведенное в степень 0, равно 1.
3. 10-2 = 1 / (10 * 10) = 0.01. Здесь показатель степени равен -2.
4. 7-3 = 1 / (7 * 7 * 7) ≈ 0.002915. Здесь показатель степени равен -3.
Показатель степени играет важную роль в математике и используется для решения различных задач, в том числе и в физике, экономике и других науках.
Степень с натуральным показателем
В математической записи степень с натуральным показателем обозначается символом «^». Например, число 2 возводится в степень 3 следующим образом: 2^3 = 2 * 2 * 2 = 8. В этом примере число 2 называется основанием, а число 3 – показателем степени.
Основная свойство степени с натуральным показателем: при умножении числа на себя столько раз, сколько указано в показателе степени, получается число, которое называется степенью. Например, 2^4 = 2 * 2 * 2 * 2 = 16.
Степень с натуральным показателем имеет несколько важных свойств:
- а * 1^n = a, где а — любое число;
- а^1 = а, где а — любое число;
- а^0 = 1, где а — любое ненулевое число;
- а^n * а^m = а^(n+m), где а — любое число, n и m — натуральные числа.
Степень с натуральным показателем широко применяется в различных областях математики, физики, химии и других точных наук. Она используется для решения уравнений, вычисления вероятностей, моделирования процессов и многих других задач.
Степень с отрицательным показателем
В математике степень с отрицательным показателем определяется как обратная операция к возведению в степень с положительным показателем. Для числа a и отрицательного целого числа n степень с отрицательным показателем обозначается как a-n.
Чтобы посчитать степень с отрицательным показателем, нужно возвести число в положительную степень и затем взять обратное значение:
- Если a не равно нулю, то a-n = 1/(an).
- Если a равно нулю, то a-n неопределено, так как нельзя разделить на ноль.
Примеры:
- Для числа 2 и показателя -3, степень с отрицательным показателем будет: 2-3 = 1/(23) = 1/8 = 0.125.
- Для числа -4 и показателя -2, степень с отрицательным показателем будет: (-4)-2 = 1/((-4)2) = 1/16 = 0.0625.
Степень с отрицательным показателем может быть полезна при решении математических задач, включая алгебру и геометрию.
Степень с рациональными показателями

Показатель степени может быть представлен в виде простой или смешанной дроби. Например, степень с показателем 2/3 означает, что основание будет возведено в кубический корень.
Степень с рациональным показателем может быть вычислена с использованием свойств степеней. Например, при возведении числа в степень сумма показателей в числителе и знаменателе будет давать итоговый показатель. То есть, a^(m/n) = (a^m)^(1/n).
Примеры степеней с рациональными показателями:
- 2^(1/2) = √2
- 4^(3/2) = √4^3 = 8
- 27^(2/3) = ∛27^2 = 9
Степень с рациональным показателем может быть полезна при решении различных математических задач, таких как вычисление корней или работы с пропорциями.
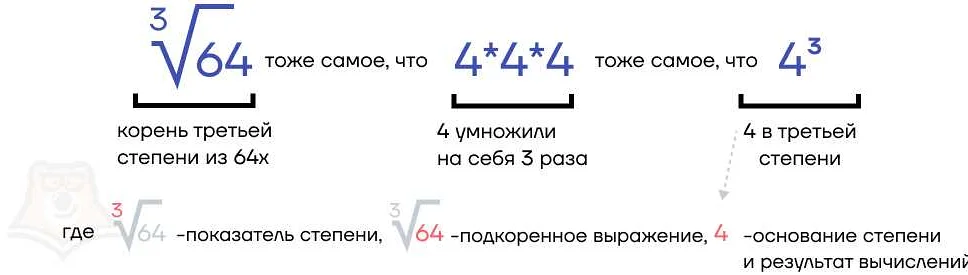
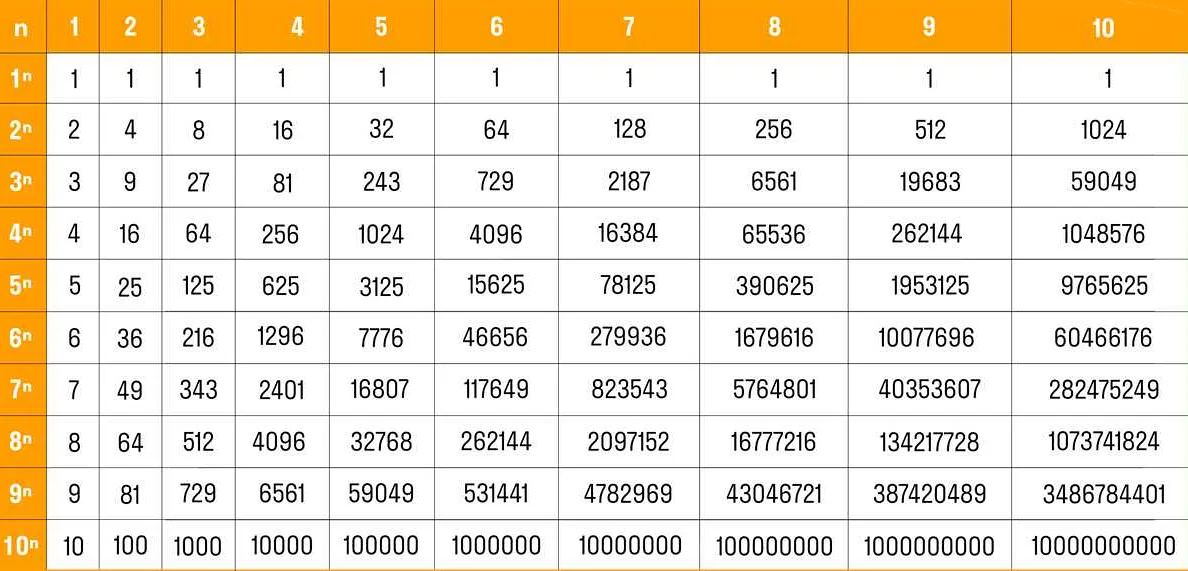
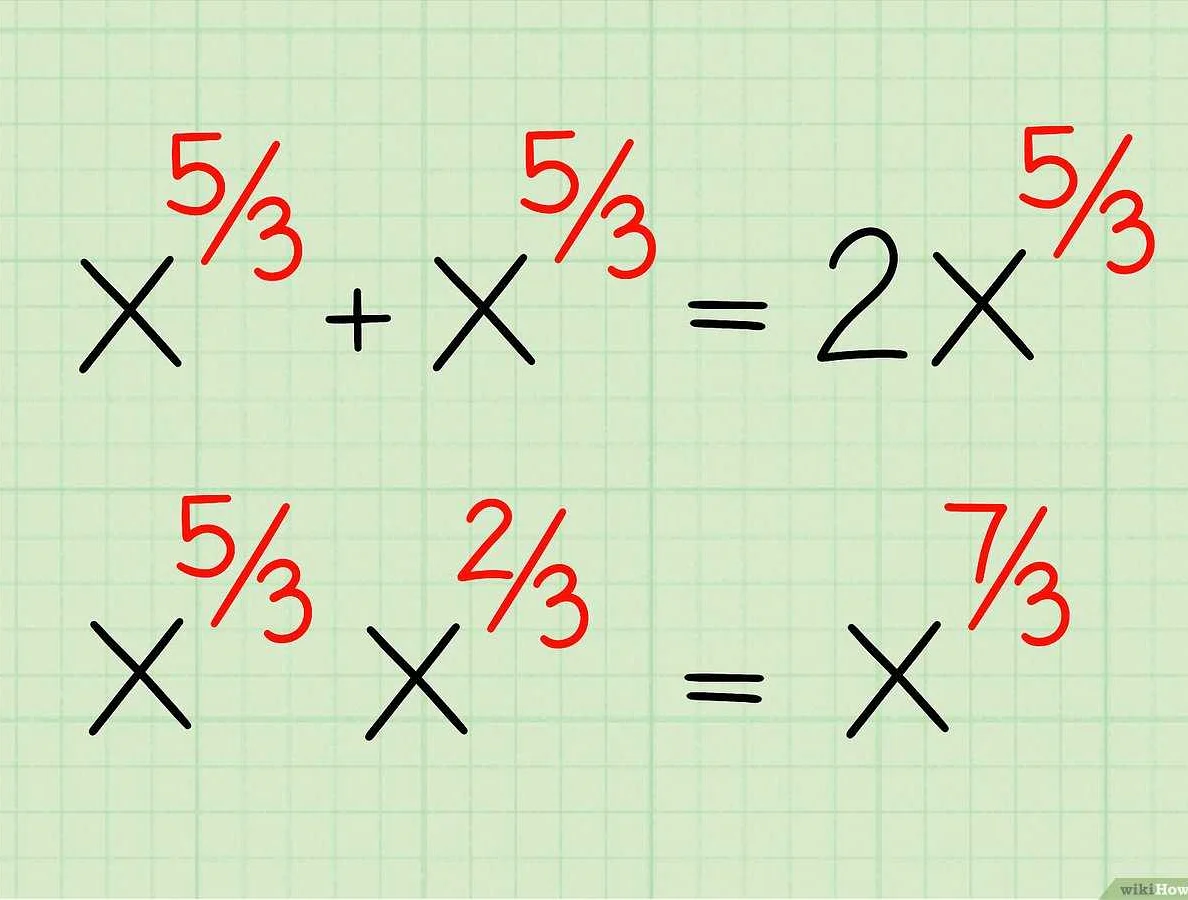
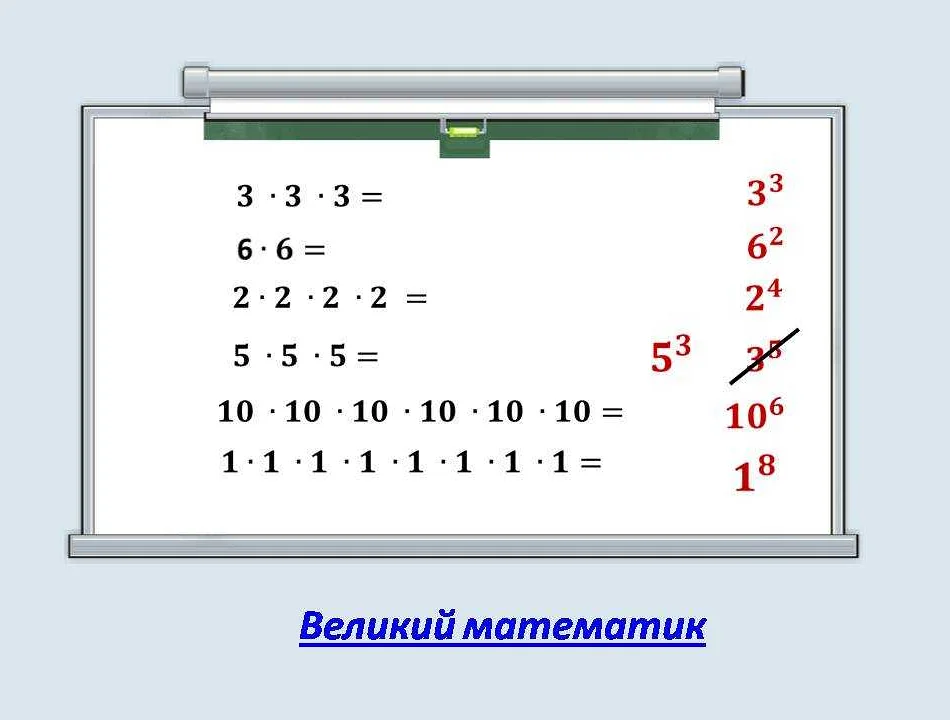
Степень в математике – это неотъемлемая часть алгебры, которая позволяет упростить вычисления и решение сложных задач. Она представляет собой операцию, где число, называемое основанием, умножается само на себя определенное количество раз, называемое показателем степени. Например, в степени 2 число умножается на себя один раз, в степени 3 – дважды, и так далее. Степени позволяют работать с большими числами более компактно и удобно. Например, 2 в степени 10 равно 1024, а 2 в степени 100 уже состоит из 31 цифры! Кроме того, степени активно используются в различных областях науки, в том числе в физике и экономике, где помогают моделировать сложные процессы и прогнозировать результаты. В общем, степени – это мощный инструмент математики, который находит применение во многих сферах жизни.
Степень в математике — это важное понятие, с которым сталкиваются все, кто изучает эту науку. Она помогает нам возводить числа в степень и выполнять различные математические операции. Степень можно представить как умножение числа самого на себя определенное количество раз. Например, 2 в степени 3 равно 2 * 2 * 2, то есть 8. Также степень может быть отрицательной или дробной, что добавляет новые интересные возможности для математических вычислений. Важно понимать, что степень имеет свои правила и свой порядок выполнения. Без понимания этих правил, можно получить неверный результат. Поэтому, для того чтобы успешно изучать математику и применять степени в реальной жизни, нужно уделить этой теме достаточно внимания и изучить все ее аспекты.
Степень в математике – это очень важный и полезный инструмент, который помогает упростить сложные вычисления и решать различные задачи. Это понятие сопровождает нас с самого начала учебы, и оно постоянно применяется не только в математике, но и в других науках, а также в повседневной жизни. Степень – это результат возведения числа в некоторую степень. Чтобы получить степень числа, нужно это число умножить само на себя определенное количество раз, указанное в показателе степени. Например, 2 в степени 3, записывается как 2³, равно 2 * 2 * 2 = 8. Степень в математике используется для решения различных задач, таких как вычисление площадей и объемов, нахождение корней уравнений, а также в финансовых расчетах и в других областях. Она позволяет упростить сложные вычисления и сделать их более понятными. Степень может быть как положительной, так и отрицательной. Если показатель степени положителен, то получаемое число будет больше исходного числа. Если показатель степени отрицателен, то получаемое число будет меньше исходного числа и будет обратным ему. Таким образом, степень – это очень важное понятие в математике, которое позволяет упростить вычисления и решать различные задачи. Понимание и умение работать со степенями помогут в повседневной жизни и в различных научных областях.
Статья очень информативная и полезная! Я всегда был немного смущен понятием «степень» в математике, и эта статья помогла мне разобраться. Теперь я понимаю, что степень — это способ записи повторяющихся умножений числа на само себя. Примеры с различными числами и степенями помогли мне лучше усвоить материал. Теперь я с уверенностью могу использовать и понимать степени в различных математических задачах. Большое спасибо за ясное объяснение!
Степень в математике — это способ записи повторяющихся умножений числа на себя. Когда я впервые столкнулся с понятием степени, мне казалось, что это сложно и непонятно. Однако, после того как я понял простое определение и увидел несколько примеров, все стало на свои места. Например, степень 2^3 означает, что нужно умножить число 2 на само себя три раза: 2 * 2 * 2 = 8. То есть, 2^3 равно 8. Это простой и понятный пример, который помог мне освоить понятие степени. Степени также могут быть отрицательными и дробными числами. Например, 2^-2 означает взятие обратного значения числа 2 в квадрате: 1/2^2 = 1/4. Также, 2^0 равно 1, потому что любое число, возведенное в степень 0, равно 1. Степень — это важное понятие в математике и используется во многих областях, включая алгебру и геометрию. Понимание степеней помогает решать сложные задачи и упрощать выражения. Мне приятно осознавать, что я могу применять это знание в повседневной жизни и решать различные математические задачи.