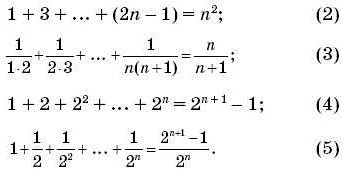Шаг и базис в математической индукции: что это такое и как использовать

Шаг и базис математической индукции — важные понятия для понимания данного метода решения задач в математике. Шагом называется переход от утверждения о k к утверждению о k+1, а базисом является проверка справедливости утверждения при k=1. Узнайте подробнее об этом методе и его применении в математике.

Математическая индукция — это один из наиболее мощных методов доказательства в математике. Он используется, когда нужно доказать утверждение для всех натуральных чисел. Этот метод состоит из двух частей: базиса и шага индукции.

Базис математической индукции — это доказательство утверждения для начального значения. Поскольку начальное значение является самым маленьким, его легко проверить, и если это верно, мы можем перейти к шагу индукции.

Шаг индукции — это доказательство, что если утверждение верно для какого-то одного целого числа n, то оно также верно и для следующего числа n+1. Это доказывается с помощью логических рассуждений на основе предположения, что утверждение верно для n.

Понимание шага и базиса математической индукции можно показать на нескольких примерах, таких как доказательство формулы суммы арифметической прогрессии, формулы бинома, а также некоторых свойств простых чисел и их кратных.

Что такое математическая индукция?

Математическая индукция — это метод доказательства утверждений, в котором для подтверждения истинности утверждения для всех натуральных чисел используются два шага:

• Базис: показывается, что утверждение верно для первого натурального числа, т.е. для n=1.
• Шаг: предполагается, что утверждение верно для некоторого натурального числа k, и доказывается, что из этого следует, что утверждение верно и для k+1.

Таким образом, используя базис и шаг, можно доказать, что утверждение верно для всех натуральных чисел.

Примером использования математической индукции может служить доказательство формулы суммы арифметической прогрессии:

• Базис: формула верна для n=1, так как в этом случае сумма состоит только из первого члена, т.е. S1=a1.
• Шаг: предположим, что формула верна для натурального числа k, т.е. Sk=k/2(a1+ak). Тогда для k+1 имеем: Sk+1 = Sk + ak+1 = k/2(a1+ak) + ak+1 = (k+1)/2(a1+ak)

Таким образом, используя базис и шаг, мы доказали формулу для всех натуральных чисел.

Как работает базис математической индукции?

Базис математической индукции — это первый шаг в доказательстве математического утверждения с помощью индукции. Базис показывает, что утверждение верно для начального значения, например, для n = 1 или n = 0.

Идея индукции состоит в том, чтобы доказать, что утверждение верно для каждого целого положительного числа n (или для всех чисел больше определенного начального значения) и, следовательно, для бесконечного числа значений n. Переход от одного значения n к следующему происходит по шагам.

Базис соответственно показывает, что первый шаг верен. Например, чтобы доказать, что сумма чисел от 1 до n равна n*(n+1)/2, нужно сначала доказать, что это верно для n = 1. Это — базис. После этого можно перейти к следующему шагу — доказательству, что утверждение верно для всех n, при условии, что это верно для n-1. Это называется шагом индукции, и он доказывается на основе предположения индукции.

Важно помнить, что базис и шаг индукции должны быть четко сформулированы, чтобы доказательство было верным. Кроме того, базис представляет собой неотъемлемую часть каждого доказательства с помощью математической индукции.

Как работает шаг математической индукции?

Шаг математической индукции — это ключевой момент при использовании метода индукции для доказательства утверждений. Суть этого метода заключается в том, чтобы из доказательства того, что утверждение верно для одного конкретного значения (базовый случай), сделать вывод о том, что утверждение верно для всех последующих значений (шаг индукции).

Для того, чтобы осуществить шаг математической индукции, необходимо сформулировать утверждение, которое хочется доказать, и разбить его на две части: базовый случай и шаг индукции.

• В базовом случае нужно показать, что утверждение верно для некоторого начального значения, как правило, самого маленького.
• В шаге индукции необходимо показать, что, если утверждение верно для некоторого числа, то оно верно и для следующего (выраженного, как правило, через увеличение значения на единицу).

Если базовый случай и шаг индукции сформулированы правильно и доказаны, то утверждение доказано для всех значений, начиная с базового. Адекватность базового случая очень важна и его выбор может зависеть от задачи и контекста ее решения.

Пример использования базиса и шага математической индукции

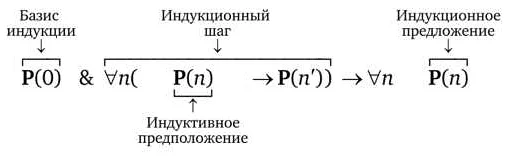
Математическая индукция — это метод доказательства утверждений в математике. Он базируется на двух основных концепциях: базисе и шаге.

Базис: Предварительное утверждение, которое необходимо доказать, называется базисом. Оно является частным случаем данного утверждения, который легко проверить непосредственно.

Шаг: Используя базис и допустив, что утверждение верно для некоторого целого числа k, нужно доказать, что оно также верно для k+1. Это называется шагом.

Рассмотрим пример использования базиса и шага математической индукции для доказательства формулы суммы последовательных чисел от 1 до n:

• Базис: Для n = 1, сумма последовательных чисел от 1 до n равна 1. Это верно, поскольку 1 = 1.
• Шаг: Предположим, что утверждение верно для некоторого числа k. Используя это предположение, докажем, что оно также верно для k+1:

ФОРМУЛА СУММЫ:

1 + 2 + … + k + (k+1) = (k+1)(k+2) / 2

Из предположения следует, что 1 + 2 + … + k = k(k+1) / 2. Подставим это выражение в формулу суммы:

1 + 2 + … + k + (k+1) =

=(k(k+1) / 2) + (k+1)	Раскрываем скобки
= (k^2 + k) / 2 + (2k+2) / 2	Общий знаменатель и сокращаем на 2
= (k^2 + 3k + 2) / 2 = (k+1)(k+2)/2	Сокращаем полученное слагаемое

Полученное утверждение соответствует формуле суммы от 1 до k+1. Следовательно, наше утверждение верно для всех натуральных чисел.

Как доказать утверждение с помощью математической индукции?

Математическая индукция — это метод доказательства утверждений о числах, на которых определена операция сложения и отношение порядка. Он состоит из двух шагов: базисного и индукционного.

Для начала необходимо проверить справедливость базисного шага, который подразумевает доказательство истинности утверждения для некоторого начального значения (обычно это ноль или единица). Если базисный шаг верен, то переходим к индукционному шагу.

Индукционный шаг доказывает, что если утверждение верно для некоторого числа, то оно верно и для следующего. Для этого необходимо предположить, что утверждение верно для некоторого f(k) и доказать, что оно верно для k + 1.

Пример доказательства с помощью математической индукции: докажем, что сумма первых n нечетных чисел равна n². Базисный шаг: если n = 1, то сумма первого нечетного числа равна 1, что равно 1². Истина базисного шага проверена.

Индукционный шаг: предположим, что утверждение верно для n = k. Докажем, что оно верно для n = k + 1. Сумма первых k нечетных чисел будет равна k², а следующее нечетное число равно 2k + 1. Суммируя эти два значения, получим:

1 + 3 + 5 + … + (2k — 1) + (2k + 1) = k² + 2k + 1 = (k + 1)²

Доказательство закончено, и по принципу математической индукции мы можем сделать вывод, что утверждение верно для всех натуральных чисел.

Пример доказательства утверждения с помощью математической индукции

Пусть у нас есть утверждение A(n), которое зависит от натурального числа n. Для доказательства этого утверждения можно использовать метод математической индукции.

Для этого нужно сделать два шага:

• Шаг базиса. Доказываем, что утверждение верно для n=1 (или для другого начального значения, если это указано в условии).
• Шаг перехода. Предполагаем, что утверждение верно для n=k и доказываем, что из этого следует, что оно верно и для n=k+1.

В качестве примера рассмотрим задачу: доказать, что для любого натурального числа n верно утверждение:

1 + 2 + 3 + … + n = n*(n+1)/2

Шаг базиса: При n=1 утверждение принимает вид 1=1*(1+1)/2, что верно.

Шаг перехода: Предположим, что утверждение верно при n=k. Нам нужно доказать, что из этого следует, что оно верно и для n=k+1.

Действительно, сумма чисел от 1 до k+1 можно разложить на сумму чисел от 1 до k и к+1:

1 + 2 + 3 + … + k + (k+1) = 1 + 2 + 3 + … + k + k+1 = k*(k+1)/2 + (k+1) = (k+1)*(k/2+1)=(k+1)*((k+1)+1)/2

Таким образом, мы доказали, что утверждение верно для любого натурального числа n исходя из того, что оно выполнено для n=1 и правильности шага перехода.

Как работает индукция второго порядка?

Индукция второго порядка – это метод математического доказательства, который используется, когда применение индукции первого порядка оказывается недостаточным для доказательства утверждения.

Для того чтобы применить индукцию второго порядка, необходимо доказать две базовые ступени, а затем показать, что любое утверждение, которое мы хотим доказать, выполнено для всех чисел, больших или равных какому-то фиксированному числу n любой из базовых ступеней.

Например, при доказательстве того, что любое натуральное число можно разложить в виде произведения простых чисел, можно использовать индукцию второго порядка. Базовые ступени можно выбрать равными 2 и 3, а затем показать, что любое натуральное число, большее 3, может быть выражено в виде произведения простых чисел.

• Шаг 1. Показываем, что любое число, большее или равное 2, может быть выражено в виде произведения простых чисел.
• Шаг 2. Показываем, что любое число, большее или равное 3, может быть выражено в виде произведения простых чисел.
• Шаг 3. Предполагаем, что любое число, большее или равное n, может быть выражено в виде произведения простых чисел.
• Шаг 4. Доказываем, что любое число, большее или равное n + 1, может быть выражено в виде произведения простых чисел.

Таким образом, применение индукции второго порядка позволяет доказать утверждения, которые не могут быть доказаны с помощью индукции первого порядка. Однако использование этого метода требуется больше усилий и внимания к деталям, поэтому его следует применять только тогда, когда это необходимо.

Пример использования индукции второго порядка

Индукция второго порядка — это метод доказательства, когда на каждом шаге индукции мы предполагаем, что утверждение верно для всех предыдущих шагов индукции, а затем доказываем его для следующего шага.

Пример использования индукции второго порядка — доказательство того, что любое дерево с n вершинами имеет n-1 ребро.

База индукции: Если n=1, то дерево состоит из одной вершины, и не имеет ребер. Таким образом, утверждение верно для n=1.

Шаг индукции: Предположим, что утверждение верно для всех деревьев с количеством вершин n меньше k. Рассмотрим дерево с k вершинами.

1. Выберем любую вершину в дереве и удалите ее, а также все ребра, связывающие ее с остальными вершинами.
2. Удалив эту вершину, мы получаем две отдельные связанные компоненты.
3. В каждой из этих компонент мы можем применить предположение индукции, т.е. утверждение верно для этих меньших деревьев.
4. После этого мы можем соединить эти компоненты общим ребром, которое связывает удаленную вершину с оставшейся частью дерева.
5. Таким образом, мы добавили одно ребро и получили дерево с k вершинами и k-1 ребром.

Таким образом, по принципу математической индукции мы доказали, что любое дерево с n вершинами имеет n-1 ребро.

Как работает индукция по натуральным числам?

Индукция по натуральным числам — это метод математического доказательства, который используется для проверки верности утверждения для всех натуральных чисел. Принцип индукции построен на двух шагах: базовом и индуктивном.

Базовый шаг — это проверка верности утверждения для самого первого натурального числа, обычно для 1 или 0. Если утверждение верно для базового случая, то переходим к следующему шагу.

Индуктивный шаг — это доказательство верности утверждения для следующего натурального числа, используя предположение, что верно для всех предыдущих чисел. Для этого необходимо представить данное натуральное число в виде суммы предыдущего числа и единицы, и применить предположение индукции.

Применение индукции позволяет доказать верность утверждения для всех натуральных чисел, что является основой многих теорий и алгоритмов в математике и информатике.

Видео по теме:

Вопрос-ответ:

Как определить шаг математической индукции?

Шаг математической индукции — это требуемое доказательство утверждения для n+1 на основе утверждения для n. В общем случае шаг индукции состоит в доказательстве того, что если утверждение верно для некоторого n, то оно верно и для n+1. Шаг индукции зависит от конкретного утверждения, которое требуется доказать.

Как определить базис математической индукции?

Базис математической индукции — это начальное утверждение, которое должно быть верно для n=1. В общем случае базис индукции требует доказательства утверждения для некоторого начального значения n (зачастую, это равно 1). Например, для доказательства утверждения «для всех натуральных чисел n сумма первых n натуральных чисел равна n(n+1)/2», базис индукции представляет собой доказательство утверждения для n=1, т.е. 1=1(1+1)/2=1.

Как часто применяется математическая индукция?

Математическая индукция — это один из наиболее распространенных методов доказательства в математике. Он используется для доказательства многих утверждений, включая теоремы, уравнения, неравенства и другие математические конструкции. В теории чисел, например, индуктивный подход к доказательству используется для доказательства сразу многих теорем и утверждений.

В каких областях математическая индукция не применима?

Математическая индукция может быть применена только для конечных последовательностей или множеств, и не может использоваться для бесконечных последовательностей или множеств. Она также не может быть использована для доказательства любых случайных утверждений, и требует, чтобы базисные и индукционные доказательства были формально доказуемы.

Как работает принцип математической индукции?

Принцип математической индукции состоит в доказательстве утверждения для всех натуральных чисел n путем доказательства утверждения для n=1 и доказательства, что если утверждение верно для некоторого n, то оно верно и для n+1. В сути, это значит, что если мы можем доказать, что утверждение при n=1 верно, и что его верность для любого n влечет его верность для n+1, то утверждение верно для всех натуральных n.

Как использовать математическую индукцию для доказательства тождества?

Для доказательства тождества с помощью математической индукции, нужно доказать, что тождество верно для n=1, а затем показать, что если выражение верно для n, то оно также верно и для n+1. Для большинства тождеств можно пользоваться правилами арифметики и алгебры, чтобы свести выражение к форме, в которой доказательство может быть проведено через математическую индукцию.

Как использовать математическую индукцию для доказательства неравенства?

Чтобы использовать математическую индукцию для доказательства неравенства, нужно доказать, что неравенство верно для n=1, а затем показать, что если оно верно для n, то оно также верно и для n+1. Кроме того, нужно показать, что неравенство является правильным для всех натуральных n, а не только для отдельных значений. Это может потребовать использования различных методов исследования чисел и знаков функций.

Примеры использования индукции по натуральным числам

Метод математической индукции широко используется в вычислительной математике. Один из примеров — доказательство формулы для суммы арифметической прогрессии:

Базис: Для случая со суммой 1 + 2 используется формула суммы первых n натуральных чисел S = n(n+1)/2, что доказывается простым подстановочным методом.

Шаг индукции: Предположим, что сумма первых n чисел равна S(n) = n(n+1)/2. Докажем, что это верно и для n+1:

S(n+1) = 1 + 2 + … + n + (n+1) = S(n) + (n+1) = (n(n+1)/2) + (n+1) = (n+1)(n+2)/2

Таким образом, доказываем формулу для суммы арифметической прогрессии для всех натуральных чисел n.

Еще один пример использования индукции — доказательство неравенства Бернулли:

Базис: Для n = 1 неравенство справедливо: 1 + x >= 1 + x.

Шаг индукции: Предположим, что (1 + x)^n >= 1 + nx для некоторого натурального числа n. Тогда для n+1:

(1 + x)^(n+1) = (1+x)^n * (1+x) >= (1+nx) * (1+x) = 1 + (n+1)x + nx^2 >= 1 + (n+1)x.

Таким образом, неравенство Бернулли справедливо для любого натурального числа n.

Как применять математическую индукцию в анализе алгоритмов?

Математическая индукция — это метод доказательства утверждений о целых числах, где сначала проверяется базис (для нашей темы — базовый случай алгоритма), а затем показывается, что если утверждение верно для некоторого числа, то оно будет верно и для следующего числа.

В анализе алгоритмов математическая индукция позволяет доказывать корректность работы алгоритма на любых входных данных. Например, для алгоритма сортировки, можно доказать, что он корректно сортирует любой набор данных, используя математическую индукцию.

Для этого необходимо показать, что алгоритм работает корректно на небольшом наборе данных (базис) и затем показать, что если алгоритм корректно работает на некотором наборе данных, то он также корректно работает и на следующем наборе данных (шаг индукции).

Для анализа алгоритмов часто используют рекуррентные формулы, которые также могут быть доказаны с помощью математической индукции. Например, для алгоритма быстрого возведения в степень можно показать, что рекуррентная формула действительно вычисляет степень числа.

Таким образом, математическая индукция является мощным инструментом для доказательства корректности работы алгоритмов. Корректность алгоритмов, доказанная с помощью математической индукции, позволяет уверенно использовать их в реальных приложениях.