Применяя метод математической индукции доказать что для любого натурального п справедливы равенства

Применяя метод математической индукции, можно доказать, что для любого натурального числа п справедливы определенные равенства. Узнайте, как применить этот метод и доказать эти равенства в данной статье.

Математическая индукция — это метод математического доказательства, который используется для проверки утверждений охватывающих все натуральные числа. Этот метод основан на двух шагах: базовом шаге и шаге индукции.

Базовый шаг — это первый шаг в доказательстве индукцией. Он заключается в проверке утверждения для первого натурального числа. Если утверждение верно для этого числа, то он считается базовым случаем.

Шаг индукции — это второй шаг в доказательстве индукцией. Он заключается в предположении, что утверждение верно для некоторого натурального числа k и доказательстве, что утверждение также верно для числа k + 1. Если это утверждение верно для всех натуральных чисел, начиная с базового случая, то оно считается верным для всех натуральных чисел.

Применение метода математической индукции широко используется для доказательства равенств. Он позволяет доказывать равенства, которые могут быть сложными для доказательства другими методами. Для этого необходимо правильно сформулировать утверждение, провести базовый шаг и шаг индукции, и в конечном итоге доказать равенство для всех натуральных чисел. Метод математической индукции является одним из основных инструментов математического доказательства и находит широкое применение в различных областях математики.

Метод математической индукции для доказательства равенств

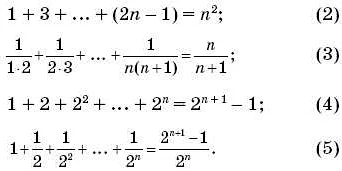
Идея метода заключается в следующем:

1. База индукции: доказываем, что равенство выполняется для некоторого начального условия (например, при n = 1).
2. Индукционный переход: предполагаем, что равенство выполняется при некотором значении n и доказываем, что оно выполняется и при n+1.

Таким образом, если равенство выполняется для базы индукции и следует из его выполнения для индукционного перехода, то оно выполняется для всех значений n.

При доказательстве равенств методом математической индукции важно следить за логической последовательностью рассуждений и строго соблюдать указанные шаги. Необходимо также учитывать допущения и ограничения, которые могут быть наложены на значения переменных.

Одна из ключевых особенностей метода математической индукции для доказательства равенств заключается в том, что он позволяет установить равенство для всех натуральных чисел, а не только для конкретного значения. Это делает его мощным инструментом в математическом анализе и дискретной математике.

Применение метода математической индукции для доказательства равенств требует аккуратности, внимательности и строгости в рассуждениях. Но при правильном применении этот метод позволяет получить строгое математическое доказательство равенств и установить их истинность для всех значений переменных.

Видео по теме:

Определение и принцип работы метода

Принцип работы метода математической индукции состоит из двух шагов:

1. База индукции: В этом шаге доказывается истинность утверждения для начального значения, обычно для наименьшего возможного числа или некоторого фиксированного значения. Это является первым шагом доказательства.
2. Шаг индукции: В этом шаге предполагается, что утверждение истинно для некоторого числа (называемого предположением индукции), и доказывается, что оно также верно и для следующего числа. Таким образом, предположение индукции распространяется на все последующие числа. Это второй шаг доказательства.

Если оба этих шага выполнены, то по принципу математической индукции утверждение считается доказанным для всех натуральных чисел или бесконечной последовательности.

Шаг базы индукции и его важность

Шаг базы индукции является фундаментом всего доказательства и его важность заключается в том, что он обеспечивает основу для последующих шагов индукции. Если шаг базы индукции выполнен корректно и утверждение верно для начального значения переменной, то можно переходить к следующему шагу индукции.

Важно провести проверку утверждения при начальном значении, чтобы убедиться, что оно действительно выполняется. Если утверждение не верно для начального значения, то оно не будет верно и для всех последующих значений переменной. Поэтому шаг базы индукции является неотъемлемой частью доказательства и необходим для его корректности.

Вопрос-ответ:

Какой метод используется для доказательства равенств?

Для доказательства равенств часто применяется метод математической индукции.

Как работает метод математической индукции?

Метод математической индукции состоит из двух этапов: базовый шаг и шаг индукции. На базовом шаге доказывается верность утверждения для некоторого начального значения. На шаге индукции доказывается, что если утверждение верно для некоторого числа, то оно верно и для следующего числа.

В каких задачах можно использовать метод математической индукции?

Метод математической индукции можно применять в задачах, где требуется доказать равенство для всех натуральных чисел или для всех целых чисел. Это может быть, например, доказательство формулы для суммы чисел, формулы для факториала, или других математических выражений.

Какие условия должны быть выполнены для применения метода математической индукции?

Для применения метода математической индукции необходимо выполнение двух условий: базовый шаг должен быть выполнен (доказано верное утверждение для начального значения), и шаг индукции должен быть выполнен (доказано, что если утверждение верно для некоторого числа, то оно верно и для следующего числа).

Как доказать равенство с помощью метода математической индукции?

Чтобы доказать равенство с помощью метода математической индукции, необходимо сначала выполнить базовый шаг — доказать верность утверждения для начального значения. Затем, на шаге индукции, нужно доказать, что если утверждение верно для некоторого числа, то оно верно и для следующего числа. Таким образом, доказательство проводится для всех чисел по порядку, начиная с начального значения.

Какой метод используется для доказательства равенств?

Для доказательства равенств часто применяется метод математической индукции. Он основан на двух шагах: базовом и индукционном. В базовом шаге нужно проверить верность утверждения для некоторого начального значения. В индукционном шаге предполагается, что утверждение верно для некоторого значения, и доказывается, что оно верно и для следующего значения. Таким образом, показывается, что утверждение верно для всех значений из рассматриваемого множества.

Как применить метод математической индукции для доказательства равенства?

Для применения метода математической индукции для доказательства равенства нужно выполнить два шага. В базовом шаге нужно доказать, что утверждение верно для начального значения (например, для n = 1). В индукционном шаге предполагается, что утверждение верно для некоторого значения n, и на этом основании доказывается, что оно верно и для следующего значения (n + 1). Таким образом, показывается, что утверждение верно для всех значений n из рассматриваемого множества.

Индукционное предположение и его формулировка

В процессе применения метода математической индукции мы формулируем индукционное предположение, которое предполагает, что утверждение верно для некоторого числа n. Затем мы доказываем, что если утверждение верно для числа n, то оно верно и для числа n+1. Таким образом, мы доказываем, что утверждение верно для всех натуральных чисел, начиная с базового случая и используя индукционное предположение.

Индукционное предположение обычно формулируется в виде утверждения: «Пусть утверждение верно для некоторого числа n». Затем в процессе доказательства индукционным методом мы предполагаем, что это утверждение верно для числа n и используем это предположение для доказательства его верности для числа n+1.

Индукционное предположение играет ключевую роль в методе математической индукции, поскольку оно позволяет нам перейти от одного числа к другому и доказать верность утверждения для всех натуральных чисел.

Шаг индукции и его роль в доказательстве

Базовый шаг заключается в проверке равенства для первого натурального числа, обычно для числа 1. Это позволяет установить базовое знание и основу для дальнейшего доказательства.

Шаг индукции представляет собой логическое рассуждение, которое позволяет перейти от одного числа к следующему. Он основан на предположении, что равенство выполняется для некоторого числа k, и доказывает, что оно выполняется и для числа k+1.

Роль шага индукции в доказательстве заключается в том, что он позволяет обобщить равенство со всеми натуральными числами. Если базовый шаг и шаг индукции выполнены корректно, то это гарантирует, что равенство выполняется для всех натуральных чисел.

Шаг индукции является мощным методом доказательства, который применяется во многих областях математики. Он позволяет установить равенства и свойства чисел, рекурсивные формулы и теоремы о последовательностях. Благодаря своей простоте и универсальности, он является одним из основных инструментов математического рассуждения и доказательства.

Доказательство базы индукции

Для этого необходимо:

1. Выбрать значение переменной, для которого будет проверяться равенство.
2. Подставить выбранное значение в выражение, которое требуется доказать.
3. Вычислить значение выражения с подставленным значением переменной и сравнить его с правой частью равенства.

Если значения совпадают, то база индукции считается доказанной и можно переходить к следующему шагу — предположению индукции. Если значения не совпадают, то требуется пересмотреть выбранное значение переменной и повторить процесс проверки.

Доказательство базы индукции является важным этапом в использовании метода математической индукции, так как оно обеспечивает начальную точку для проведения индуктивного рассуждения и доказательства равенств.

Доказательство шага индукции

1. База индукции: сначала доказывается равенство для начального значения переменной. Это является первым шагом в методе математической индукции.
2. Шаг индукции: предполагая, что равенство выполняется для некоторого значения переменной, необходимо доказать, что оно также выполняется для следующего значения переменной.

Доказательство шага индукции обычно выполняется следующим образом:

1. Предположим, что равенство выполняется для некоторого значения переменной (это называется предположением индукции).
2. Используя предположение индукции, докажем, что равенство также выполняется для следующего значения переменной.
3. В результате доказательства, равенство будет справедливым для всех значений переменной, начиная с базы индукции.

Доказательство шага индукции является основной частью метода математической индукции, так как оно позволяет расширить доказательство равенства на все значения переменной. Благодаря этому шагу, можно доказать равенства для бесконечного количества значений переменной, основываясь только на базе индукции и предположении индукции.

Применение метода математической индукции для сложных равенств

Для применения метода математической индукции к сложным равенствам необходимо следовать нескольким шагам:

1. База индукции: доказать, что равенство выполняется для начального значения, обычно это наименьшее возможное значение переменной.
2. Предположение индукции: предположить, что равенство выполняется для некоторого значения переменной.
3. Индукционный переход: доказать, что если равенство выполняется для некоторого значения переменной, то оно также выполняется для следующего значения переменной.

Применение метода математической индукции для сложных равенств требует внимательности и логического мышления. Однако, благодаря своей стройности и формальности, этот метод является эффективным инструментом для доказательства равенств, включая те, которые могут быть сформулированы в виде сложных уравнений или неравенств.

Важно отметить, что применение метода математической индукции требует точности и внимания к деталям. Необходимо четко формулировать базу индукции, предположение индукции и индукционный переход, а также логически связывать каждый шаг доказательства. Это позволяет установить строгую логическую цепочку, которая гарантирует правильность доказательства равенства.

Ограничения и преимущества метода

Ограничения:

1. Ограниченность применения: Метод математической индукции применим только для доказательства равенств, которые можно записать в виде утверждений, зависящих от натурального числа. Другие типы утверждений, такие как неравенства или исключительные случаи, требуют других методов доказательства.

2. Зависимость от базового случая: В методе математической индукции необходимо доказать базовый случай, который является основой для последующих шагов индукции. Если базовый случай неверен или недоказуем, то весь доказательство становится недействительным.

Преимущества:

1. Простота и ясность: Метод математической индукции предлагает простой и понятный подход к доказательству равенств. Он использует логические рассуждения, что делает его понятным даже для начинающих математиков.

2. Универсальность: Метод математической индукции может быть применен для доказательства равенств во многих областях математики, включая алгебру, комбинаторику, теорию чисел и дискретную математику. Это делает его универсальным инструментом для математических исследований.

В целом, метод математической индукции является надежным и эффективным способом доказательства равенств в математике. Однако, его применимость ограничена определенными типами утверждений, и он требует внимательности при выборе базового случая.