Что такое треугольник математика 5 класс

Треугольник в математике 5 класса — это геометрическая фигура, состоящая из трех отрезков, соединенных их концами. В данной статье вы узнаете основные понятия и свойства треугольника, а также способы решения задач на его построение и измерение углов.

Треугольник — это основная геометрическая фигура, состоящая из трех сторон и трех углов. Он является одним из первых объектов, с которыми знакомятся учащиеся в курсе математики 5 класса. Понимание основных понятий, свойств и формул, связанных с треугольником, является важной составляющей математического образования в начальной школе.

Одно из основных понятий связанных с треугольником — это его стороны. В треугольнике есть три стороны — это отрезки, которые соединяют вершины треугольника. Обычно стороны треугольника обозначают заглавными буквами A, B и C, а длины сторон обозначают маленькими буквами a, b и c.

Кроме сторон, треугольник имеет три угла. Углы обозначаются маленькими греческими буквами: α, β и γ. Сумма углов треугольника всегда равна 180 градусам. Это свойство называется суммой углов треугольника и является одним из основных свойств треугольника, которое необходимо знать.

Помимо сторон и углов, треугольник имеет и другие важные характеристики, такие как периметр и площадь. Периметр треугольника — это сумма длин всех его сторон. Площадь треугольника — это мера его плоской поверхности и вычисляется с помощью специальной формулы, зависящей от его сторон и углов.

В заключение, понимание основных понятий и свойств треугольника является важным шагом в учебном процессе учеников 5 класса. Это позволяет учащимся строить и анализировать треугольники, решать задачи на их основе и применять полученные знания в практических ситуациях.

Что такое треугольник математика 5 класс?

Треугольники могут иметь разные типы и свойства. Одно из основных свойств треугольников — сумма всех его углов равна 180 градусам. Также треугольники могут быть разделены на различные типы в зависимости от длин сторон и углов.

Некоторые типы треугольников, которые изучают в 5 классе:

Тип треугольникаОписание

Равносторонний треугольник	Треугольник, у которого все стороны равны
Равнобедренный треугольник	Треугольник, у которого две стороны равны
Прямоугольный треугольник	Треугольник, у которого один из углов равен 90 градусам

Треугольники также могут быть разделены на остроугольные, тупоугольные и прямоугольные в зависимости от величины их углов.

Изучение треугольников позволяет учащимся развивать навыки визуализации, анализа и решения геометрических задач. Они также помогают ученикам понять основные принципы и приложения геометрии в реальном мире.

Основные понятия

В треугольнике можно выделить следующие основные понятия:

ПонятиеОписание

Сторона	Отрезок, соединяющий две вершины треугольника.
Вершина	Точка, где сходятся две стороны треугольника.
Угол	Фигура, образованная двумя сторонами треугольника, соединяющими одну и ту же вершину.
Высота	Отрезок, соединяющий вершину треугольника с противоположной стороной и перпендикулярный этой стороне.
Медиана	Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса	Прямая, делящая угол треугольника на два равных угла.
Окружность вписанная	Окружность, которая касается всех сторон треугольника.
Окружность описанная	Окружность, которая проходит через все вершины треугольника.

Эти понятия помогают описать и изучить различные свойства и связи между элементами треугольника.

Стороны и углы

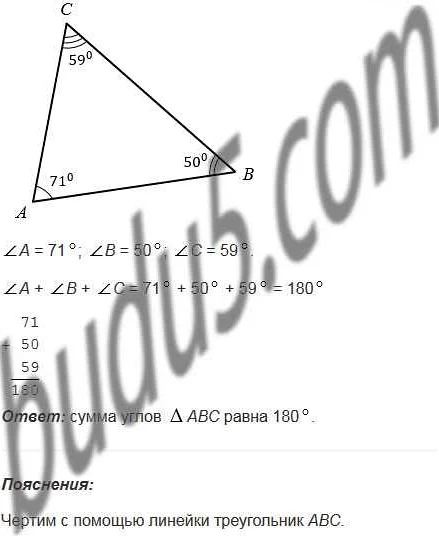
В треугольнике есть три стороны и три угла. Стороны треугольника обозначаются буквами a, b и c, а углы обозначаются буквами A, B и C.

Сторона a соответствует углу A, сторона b соответствует углу B, а сторона c — углу C.

Сумма углов треугольника всегда равна 180 градусов. Это означает, что угол A + угол B + угол C = 180°.

Также стороны треугольника могут быть классифицированы по длине:

• равносторонний треугольник — все стороны равны между собой;
• равнобедренный треугольник — две стороны равны между собой;
• разносторонний треугольник — все стороны различны.

Определение типа треугольника может быть полезным при решении задач и нахождении его свойств.

Площадь и периметр

Для вычисления площади треугольника существует несколько способов, одним из которых является использование формулы Герона. Формула Герона основана на полупериметре треугольника (половина суммы длин его сторон) и длинах его сторон. Другим распространенным способом вычисления площади треугольника является использование высоты и основания треугольника.

Что касается периметра треугольника, то его можно вычислить, сложив длины всех его сторон. Если известны длины сторон треугольника, то периметр можно найти, сложив эти длины. Если же известны координаты вершин треугольника в декартовой системе координат, то периметр можно найти, используя формулу расстояния между двумя точками на плоскости.

Площадь и периметр треугольника являются важными характеристиками при изучении геометрии и решении задач. Они помогают определить размеры треугольника и сравнить его с другими фигурами.

Разновидности треугольников

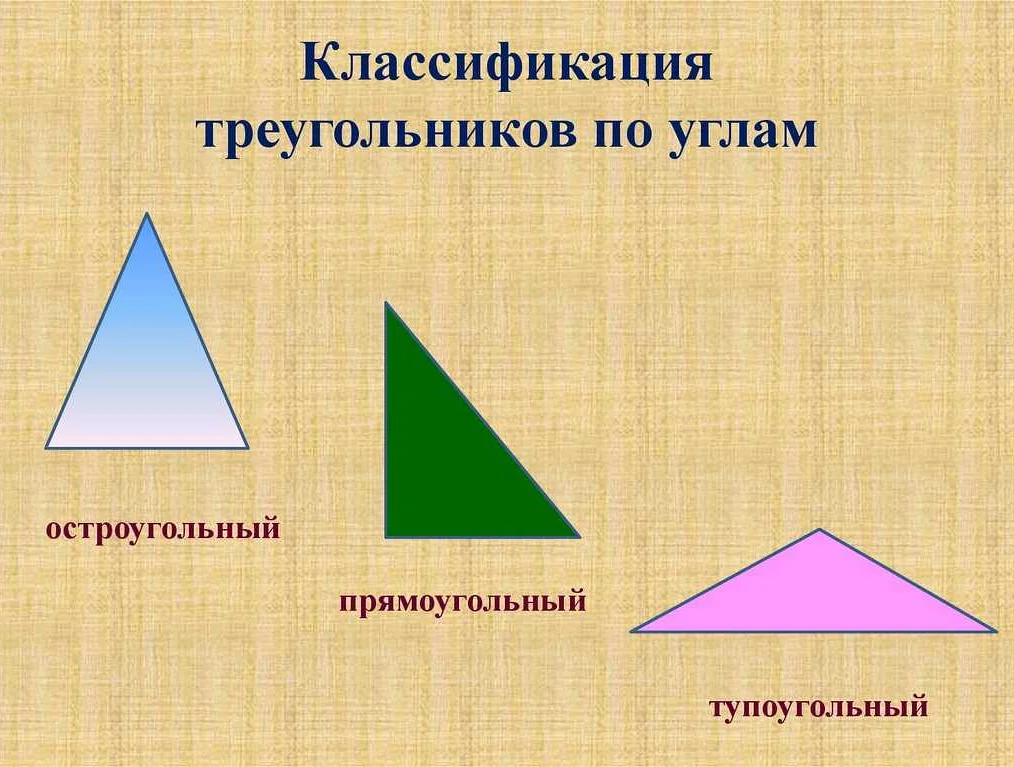
В математике существует несколько разновидностей треугольников, которые отличаются своими особенностями и свойствами. Ниже приведены основные типы треугольников:

1. Равносторонний треугольник: все три стороны и все три угла равны между собой. Углы равностороннего треугольника всегда равны 60 градусов.
2. Равнобедренный треугольник: две стороны и два угла равны между собой. В таком треугольнике две стороны, выходящие из одной вершины, равны, а углы, расположенные напротив этих сторон, равны.
3. Прямоугольный треугольник: один из углов равен 90 градусам. В прямоугольном треугольнике самая длинная сторона называется гипотенузой, а остальные две стороны — катетами.
4. Остроугольный треугольник: все углы треугольника остроугольные, т.е. меньше 90 градусов.
5. Тупоугольный треугольник: один из углов треугольника тупоугольный, т.е. больше 90 градусов.

Знание разных типов треугольников помогает нам понять и анализировать их свойства и особенности. В дальнейшем, мы будем использовать эти знания для решения задач и построения геометрических фигур.

Равнобедренный треугольник

Основными свойствами равнобедренного треугольника являются:

• У равнобедренного треугольника две равные стороны (боковые стороны) и одна отличная (основание).
• Угол между боковыми сторонами называется углом при основании.
• Углы при основании равны между собой.

Также для равнобедренного треугольника выполняются следующие свойства:

• Медиана, проведенная из вершины треугольника к основанию, является биссектрисой и высотой треугольника.
• Высота, проведенная из вершины треугольника к основанию, делит треугольник на два равных прямоугольных треугольника.
• Углы, лежащие против боковых сторон, являются смежными.

Равнобедренные треугольники встречаются в различных геометрических конструкциях и задачах, поэтому знание основных свойств равнобедренного треугольника очень важно.

Равносторонний треугольник

Основные свойства равностороннего треугольника:

1. Все стороны равны между собой.
2. Все углы равны 60 градусов.
3. Высота, проведенная из вершины равностороннего треугольника, является медианой и биссектрисой.
4. Центр описанной окружности равностороннего треугольника совпадает с его центром.

Формула для вычисления площади равностороннего треугольника:

S = (a^2 * √3) / 4,

где S — площадь, a — длина стороны.

Равносторонний треугольник является основой для изучения других типов треугольников и обладает рядом интересных свойств и применений в геометрии.

Прямоугольный треугольник

В прямоугольном треугольнике можно выделить следующие элементы:

1. Гипотенуза — это сторона треугольника, напротив прямого угла.
2. Катеты — это две оставшиеся стороны треугольника.
3. Высота — это отрезок, проведенный из вершины прямого угла к противоположной стороне.
4. Медиана — это отрезок, соединяющий вершину прямого угла с серединой гипотенузы.
5. Биссектриса — это отрезок, проведенный из вершины прямого угла к середине гипотенузы.
6. Окружность, описанная вокруг треугольника, называется описанной окружностью.

Прямоугольные треугольники широко применяются в геометрии и тригонометрии для решения различных задач и вычислений, таких как нахождение длины сторон и углов треугольника, расчет площади и периметра треугольника, а также для решения простых и сложных задач на тригонометрические функции.

Вопрос-ответ:

Что такое треугольник?

Треугольник — это геометрическая фигура, состоящая из трех сторон и трех углов.

Как классифицируются треугольники?

Треугольники могут быть классифицированы по разным параметрам, например, по длинам сторон (равносторонний, равнобедренный, разносторонний) или по величине углов (остроугольный, тупоугольный, прямоугольный).

Что такое равнобедренный треугольник?

Равнобедренный треугольник — это треугольник, у которого две стороны равны между собой. Такой треугольник имеет два равных угла, расположенных напротив равных сторон.

Как найти площадь треугольника?

Площадь треугольника можно найти, используя формулу: S = 0.5 * a * h, где a — длина основания треугольника, h — высота треугольника, проведенная к основанию.

Треугольник и его свойства

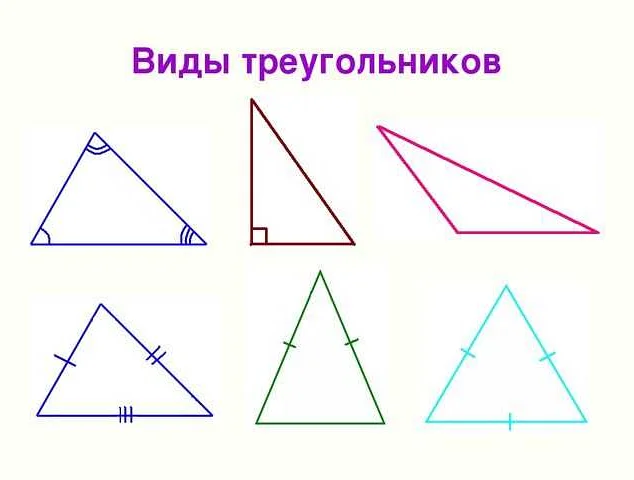
Основные понятия, связанные с треугольником:

Стороны треугольника	Треугольник имеет три стороны, которые могут быть разной длины.
Углы треугольника	Треугольник имеет три угла, которые суммируются в 180 градусов.
Равнобедренный треугольник	Треугольник, у которого две стороны равны между собой.
Равносторонний треугольник	Треугольник, у которого все три стороны равны между собой.
Прямоугольный треугольник	Треугольник, у которого один из углов равен 90 градусам.

Треугольники могут иметь различные комбинации свойств и могут быть использованы для решения разнообразных задач, как в математике, так и в реальной жизни.

Видео по теме: