Что означает знак треугольника в математике

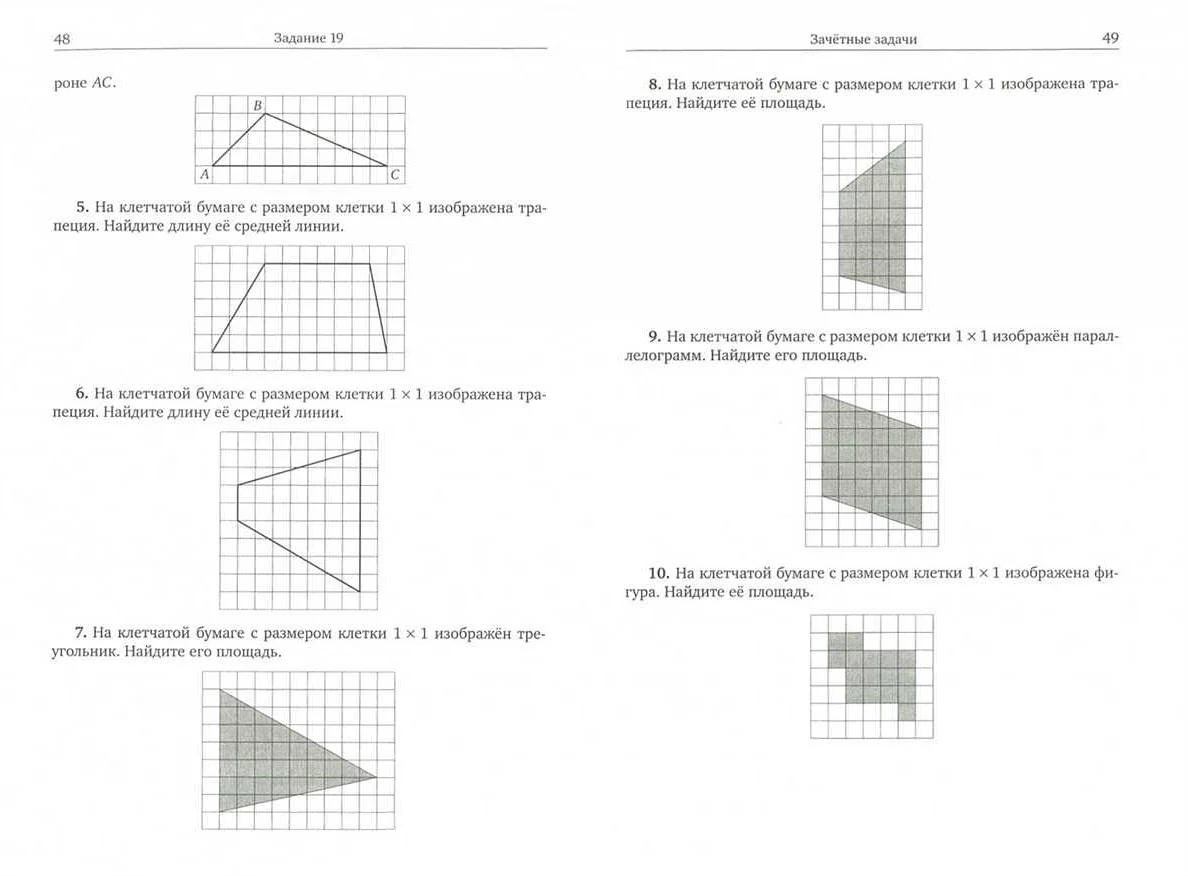
Знак треугольника в математике обычно указывает на свойства и отношения между сторонами и углами треугольника, а также на специфические формулы и теоремы, связанные с этой геометрической фигурой.

Треугольник — это одна из основных фигур в геометрии, состоящая из трех сторон и трех вершин. Треугольники широко используются в математике и имеют большое значение, как в теории, так и в практических приложениях.

Основные понятия, связанные с треугольником, включают его стороны, углы, высоты, медианы и перпендикуляры. Стороны треугольника могут быть разной длины, а углы могут быть разного размера. Высоты — это отрезки, проведенные из вершин треугольника и перпендикулярные противоположным сторонам. Медианы — это отрезки, соединяющие вершины треугольника с серединами противоположных сторон. И перпендикуляры — это линии, пересекающие стороны треугольника под прямым углом.

Треугольники имеют множество применений в различных областях науки и инженерии. Например, геодезия использует треугольники для измерения расстояний и определения формы земной поверхности. Архитектура и строительство используют треугольники для расчета прочности и стабильности конструкций. Графика и компьютерная графика используют треугольники для отображения трехмерных объектов и создания реалистичных изображений.

Треугольники также являются основой для многих других фигур и форм, и изучение их свойств и отношений играет важную роль в математике.

В заключение, треугольники являются важными объектами в математике и имеют широкое применение в различных областях. Изучение и понимание основных понятий, связанных с треугольниками, помогает в решении различных задач и проблем, а также расширяет наши знания о математике и ее приложениях.

Определение и свойства треугольника

Основные свойства треугольника:

1.	Сумма всех углов треугольника равна 180 градусам.
2.	Наибольшая сторона треугольника называется гипотенузой. Для прямоугольного треугольника гипотенуза соответствует стороне, противолежащей прямому углу.
3.	Треугольник может быть равносторонним, равнобедренным или разносторонним. Равносторонний треугольник имеет все стороны и углы равными. Равнобедренный треугольник имеет две равные стороны и два равных угла. Разносторонний треугольник имеет все стороны и углы различными.
4.	Сумма длин двух сторон треугольника всегда больше длины третьей стороны, в противном случае треугольник не существует.
5.	Высота треугольника — это линия, проведенная из вершины треугольника к основанию, перпендикулярно основанию. Высоты треугольника могут быть внутренними или внешними.

Знание определения и свойств треугольника является основой для изучения его различных свойств, формул и методов решения задач в геометрии и тригонометрии.

Видео по теме:

Различные типы треугольников

В математике есть несколько различных типов треугольников, каждый из которых имеет свои особенности и свойства. Ниже приведены основные типы треугольников:

• Равносторонний треугольник: все стороны равны между собой, а все углы равны 60 градусов.
• Равнобедренный треугольник: имеет две равные стороны и два равных угла.
• Прямоугольный треугольник: имеет один прямой угол, равный 90 градусов.
• Остроугольный треугольник: все углы острые, меньше 90 градусов.
• Тупоугольный треугольник: один угол больше 90 градусов.

Каждый из этих типов треугольников имеет свои уникальные свойства и характеристики, которые могут быть использованы для решения задач и проблем в математике и других областях науки.

Основные элементы треугольника

Основные элементы треугольника:

• Стороны: треугольник имеет три стороны, обозначаемые обычно буквами a, b и c. Сумма длин двух сторон всегда больше, чем длина третьей стороны, иначе треугольник не может существовать.
• Углы: треугольник имеет три угла, обозначаемые обычно буквами A, B и C. Сумма углов треугольника всегда равна 180 градусов.
• Высоты: треугольник имеет три высоты — отрезки, проведенные из вершины треугольника к противоположной стороне, перпендикулярные этой стороне.
• Медианы: треугольник имеет три медианы — отрезки, соединяющие вершину треугольника с серединой противоположной стороны.
• Биссектрисы: треугольник имеет три биссектрисы — линии, делящие углы треугольника на две равные части.
• Окружность вписанная: треугольник имеет вписанную окружность, которая касается всех трех сторон треугольника.
• Окружность описанная: треугольник имеет описанную окружность, которая проходит через все три вершины треугольника.

Эти элементы треугольника играют важную роль в решении геометрических задач и определении его свойств, таких как площадь, периметр, высоты, медианы, биссектрисы и т.д.

Вопрос-ответ:

Что такое треугольник?

Треугольник — это геометрическая фигура, которая состоит из трех линейных отрезков, называемых сторонами, и трех углов. У треугольника есть три вершины, где стороны соединяются.

Какие бывают треугольники по сторонам?

Треугольники могут быть различными по длине своих сторон. Есть равносторонние треугольники, у которых все стороны равны, равнобедренные треугольники, у которых две стороны равны, и разносторонние треугольники, у которых все три стороны разные.

Какие бывают треугольники по углам?

Треугольники могут быть различными по значениям своих углов. Есть остроугольные треугольники, у которых все углы меньше 90 градусов, тупоугольные треугольники, у которых один угол больше 90 градусов, и прямоугольные треугольники, у которых один угол равен 90 градусов.

Как вычислить площадь треугольника?

Площадь треугольника можно вычислить, зная длину двух его сторон и значение угла между этими сторонами. Формула для вычисления площади треугольника — это половина произведения длины одной стороны на длину другой стороны и синуса угла между ними.

Где применяются треугольники в математике?

Треугольники используются во многих областях математики. Они являются основой для изучения геометрии, тригонометрии и многих других математических дисциплин. Треугольники также широко применяются в строительстве, архитектуре, физике и других науках.

Стороны треугольника

В треугольнике существуют три стороны: a, b и c. Сторона a соединяет вершины A и B, сторона b — вершины B и C, а сторона c — вершины C и A. Каждая сторона имеет длину, которая определяется как расстояние между соответствующими вершинами.

Стороны треугольника могут быть различной длины. Треугольник, у которого все три стороны равны, называется равносторонним треугольником. Если две стороны треугольника равны, то треугольник называется равнобедренным. В противном случае треугольник называется разносторонним.

Знание длин сторон треугольника позволяет решать множество задач, связанных с его построением, вычислением площади, нахождением углов и другими геометрическими вопросами. Стороны треугольника также используются для определения его типа и свойств, что является важным аспектом в математике и других науках.

Углы треугольника

Углы треугольника определяются точками пересечения его сторон и могут быть различных типов:

• Острый угол — угол, меньший 90 градусов.
• Прямой угол — угол, равный 90 градусам.
• Тупой угол — угол, больший 90 градусов, но меньше 180 градусов.
• Равнобедренный угол — угол, у которого две стороны равны.
• Разносторонний угол — угол, у которого все три стороны различны.

Сумма углов треугольника всегда равна 180 градусам. Это свойство треугольников называется «сумма углов треугольника».

Знание углов треугольника позволяет решать различные задачи, связанные с этой геометрической фигурой, например, находить длины сторон треугольника, находить площадь треугольника или находить высоты треугольника.

Формулы и теоремы, связанные с треугольником

Одной из таких формул является формула площади треугольника. Площадь треугольника можно вычислить, зная длины двух его сторон и угол между ними. Формула площади треугольника выглядит следующим образом:

ФормулаОписание

S = (1/2) * a * b * sin(C)

Площадь треугольника, где a и b — длины сторон треугольника, C — угол между этими сторонами.

Еще одной важной теоремой, связанной с треугольником, является теорема Пифагора. Она утверждает, что квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин его катетов. Формула теоремы Пифагора выглядит следующим образом:

Теорема ПифагораОписание

c^2 = a^2 + b^2

Где c — длина гипотенузы, a и b — длины катетов прямоугольного треугольника.

Также следует отметить формулу для вычисления высоты треугольника. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к основанию. Формула для вычисления высоты треугольника зависит от известных данных о треугольнике:

ФормулаОписание

h = (2 * S) / a

Высота треугольника, где S — площадь треугольника, a — длина основания треугольника.

Это лишь некоторые из формул и теорем, связанных с треугольником. Они являются основой для решения задач и применяются в различных областях математики и физики.

Теорема Пифагора

Согласно теореме Пифагора, квадрат длины гипотенузы (самой длинной стороны) прямоугольного треугольника равен сумме квадратов длин катетов (двух других сторон).

Математическое выражение теоремы Пифагора выглядит следующим образом:

c2 = a2 + b2

Где c — длина гипотенузы, a и b — длины катетов.

Теорема Пифагора находит широкое применение в различных областях, таких как геометрия, физика и инженерия. Например, она используется при решении задач на определение расстояний и вычисления площадей фигур.

Также теорема Пифагора является основой для других математических теорем и формул, связанных с прямоугольными треугольниками, например, теоремы синусов и косинусов.

Теорема синусов и косинусов

Теорема синусов устанавливает следующую зависимость: отношение длины стороны треугольника к синусу противолежащего ей угла равно отношению длины другой стороны к синусу противолежащего ей угла.

Формула теоремы синусов имеет вид:

• $$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$$

где a, b, c — длины сторон треугольника, A, B, C — соответствующие углы.

Теорема косинусов связывает длины сторон треугольника с косинусами его углов. Она формулируется следующим образом: квадрат длины стороны треугольника равен сумме квадратов длин остальных двух сторон минус дважды произведение этих длин на косинус соответствующего угла.

Формула теоремы косинусов имеет вид:

• $$c^2 = a^2 + b^2 — 2ab\cos C$$

где a, b, c — длины сторон треугольника, C — соответствующий угол.

Теоремы синусов и косинусов широко применяются в решении различных геометрических и тригонометрических задач, а также во многих научных и инженерных областях.

Применение треугольника в реальной жизни

• Архитектура: Треугольники используются при проектировании и строительстве зданий. Они помогают определить форму и пропорции здания, а также распределить нагрузку и создать устойчивую конструкцию.
• Навигация: В навигации на море и воздухе треугольники используются для определения расстояния и направления между двумя точками, а также для вычисления скорости и времени пути.
• Тригонометрия: Треугольники играют важную роль в тригонометрии, науке, изучающей отношения между углами и сторонами треугольника. Тригонометрические функции, такие как синус, косинус и тангенс, широко используются в физике, инженерии и других науках.
• Картография: Треугольники используются при создании карт и планов местности. Путем измерения углов и расстояний между треугольниками можно построить точную карту местности.
• Графика и компьютерная графика: Треугольники являются основными элементами в графике и компьютерной графике. Они используются для создания трехмерных моделей, определения формы и размеров объектов, а также для создания гладких поверхностей.
• Инженерия: В инженерии треугольники используются для решения различных задач. Они помогают определить направление и угол наклона грунта при строительстве дорог и зданий, а также при проведении геодезических измерений.

Это лишь некоторые примеры использования треугольника в реальной жизни, и его значение и применение охватывают множество других областей.

Инженерия и архитектура

В инженерии треугольники используются для вычисления расстояний, углов и площадей. Например, в геодезии треугольники используются для измерения расстояний между точками на земной поверхности и определения их координат. В строительстве треугольники используются для построения фундаментов, стен и других конструкций.

В архитектуре треугольники используются для создания прочных и устойчивых конструкций. Треугольники являются стабильными и прочными фигурами, поэтому они широко применяются в архитектурных проектах. Они используются для построения каркасов зданий, арок, куполов и других элементов архитектуры.

Кроме того, треугольники используются в компьютерной графике и дизайне. Они являются основными элементами для создания трехмерных моделей, анимаций и графических эффектов.

Таким образом, треугольники имеют большое значение в инженерии и архитектуре. Они являются основным инструментом для решения различных задач и создания прочных и эстетичных конструкций.