Что такое треугольник в математике 5 класс

Узнайте, что такое треугольник в математике для ученика 5 класса. Разберитесь с его определением, свойствами и типами треугольников. Подробно изучите формулы для вычисления периметра и площади треугольника. Получите полезные советы и примеры задач для углубленного понимания этой фигуры.

Треугольник — это плоская геометрическая фигура, состоящая из трех отрезков, называемых сторонами, и трех точек, называемых вершинами. Для того чтобы треугольник существовал, сумма длин любых двух его сторон должна быть больше длины третьей стороны.

В математике 5 класса треугольники рассматриваются в рамках изучения геометрии. Одной из основных целей изучения треугольников является определение их свойств. Основные свойства треугольников включают такие понятия, как углы, стороны, высоты и медианы.

Углы треугольника — это углы, образованные его сторонами. Сумма углов треугольника всегда равна 180 градусам. Также треугольники могут быть различных типов в зависимости от величины их углов. Например, прямоугольный треугольник имеет один прямой угол, равный 90 градусам.

Стороны треугольника — это отрезки, соединяющие его вершины. Стороны треугольника могут быть разной длины, что определяет его форму. Например, равнобедренный треугольник имеет две равные стороны.

Высоты и медианы треугольника — это отрезки, соединяющие вершины треугольника с противоположными сторонами и их середины соответственно. Высоты и медианы являются важными элементами треугольника и помогают в решении различных задач и нахождении его площади.

Знание основных свойств треугольников позволяет анализировать и решать задачи, связанные с этой геометрической фигурой. Понимание углов, сторон, высот и медиан треугольника является важным шагом в изучении математики и развитии логического мышления.

Определение треугольника в математике

Треугольник обозначается обычно буквами A, B и C, которые соответствуют его вершинам. Стороны треугольника обозначаются маленькими буквами a, b и c, а углы — заглавными буквами A, B и C, соответственно.

Примеры треугольников:

— Равносторонний треугольник имеет все стороны одинаковой длины и все углы равны 60 градусам.

— Равнобедренный треугольник имеет две равные стороны и два равных угла.

— Прямоугольный треугольник имеет один прямой угол (90 градусов).

Треугольники в математике широко используются для решения задач и анализа геометрических взаимосвязей. Изучая треугольники, можно определить их свойства, вычислить значения углов и сторон, а также провести различные геометрические построения.

Основные свойства треугольника

Основные свойства треугольника:

• Сумма внутренних углов треугольника всегда равна 180 градусам.
• Сумма длин любых двух сторон треугольника всегда больше длины третьей стороны.
• Наибольшая сторона треугольника всегда лежит против наибольшего угла, а наименьшая сторона — против наименьшего угла.
• Высота треугольника — это перпендикуляр, опущенный из вершины к противолежащей стороне.
• Медиана треугольника — это отрезок, соединяющий вершину с серединой противолежащей стороны.
• Биссектриса треугольника — это отрезок, делящий угол на два равных угла.

Знание основных свойств треугольника позволяет решать различные задачи, связанные с измерением углов, длин сторон и высот треугольника.

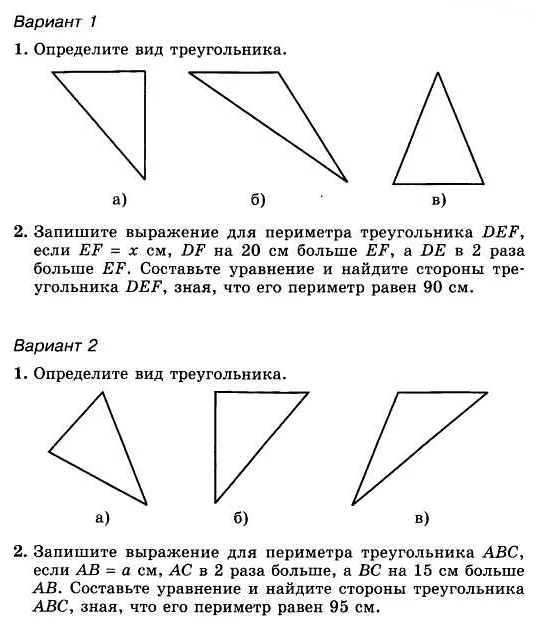
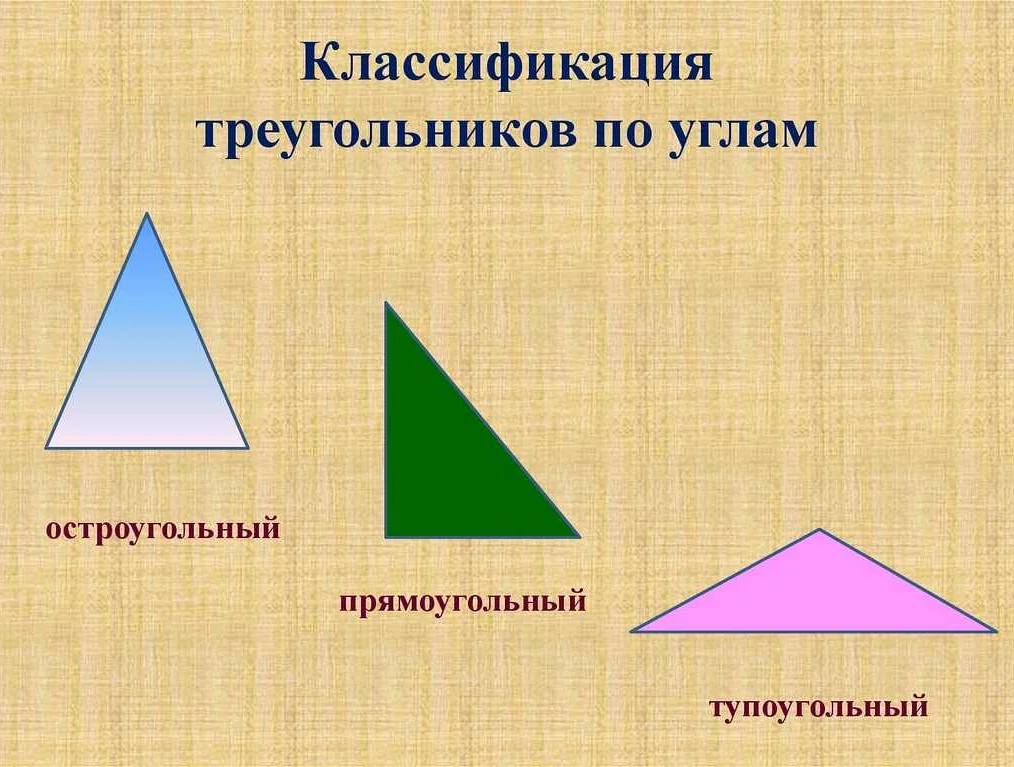
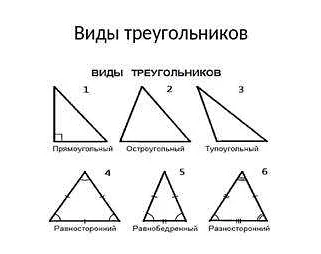
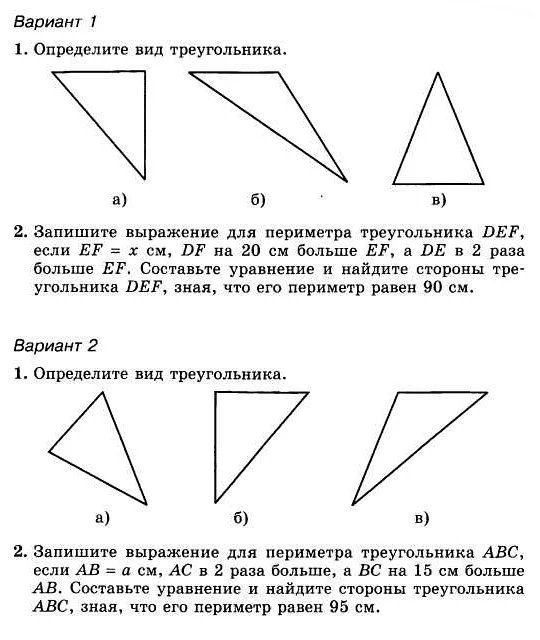
Разновидности треугольников

В математике существуют различные разновидности треугольников, которые отличаются своими свойствами и характеристиками.

Основные разновидности треугольников:

• Равносторонний треугольник — треугольник, у которого все стороны равны.
• Равнобедренный треугольник — треугольник, у которого две стороны равны.
• Прямоугольный треугольник — треугольник, у которого один из углов является прямым углом, то есть равен 90 градусам.
• Остроугольный треугольник — треугольник, у которого все углы острые, то есть меньше 90 градусов.
• Тупоугольный треугольник — треугольник, у которого один из углов является тупым углом, то есть больше 90 градусов.

Каждая разновидность треугольника имеет свои особенности и характеристики, которые определяются его сторонами и углами. Изучение этих разновидностей позволяет лучше понять и анализировать свойства и особенности треугольников в математике.

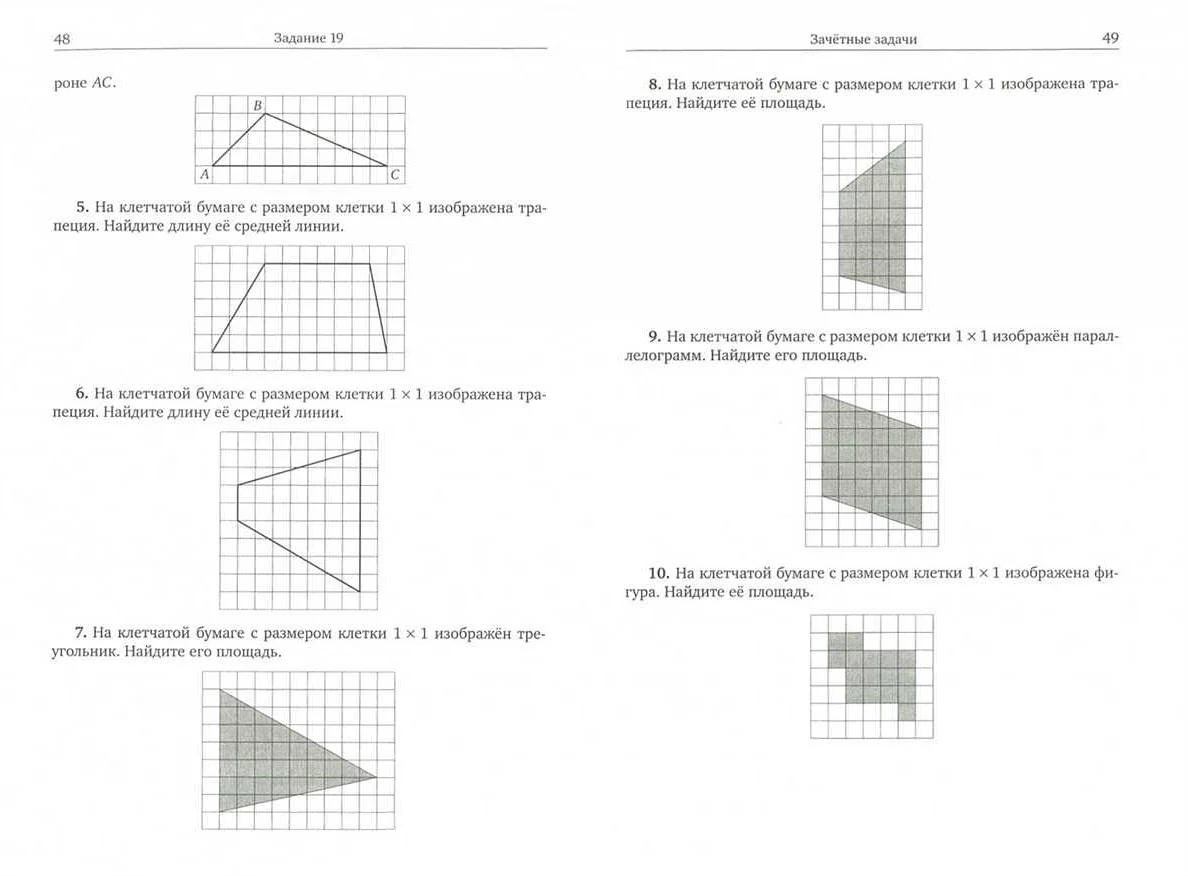
Формулы для вычисления площади треугольника

Если известны длины основания треугольника (a) и высота, опущенная на это основание (h), то площадь (S) может быть найдена по формуле:

ФормулаОписание

S = (a * h) / 2

Формула для вычисления площади треугольника по основанию и высоте

Если известны длины всех трех сторон треугольника (a, b, c), то площадь (S) может быть найдена по формуле Герона:

ФормулаОписание

S = √(p * (p — a) * (p — b) * (p — c))	Формула Герона для вычисления площади треугольника по длинам сторон
p = (a + b + c) / 2	Полупериметр треугольника

По формулам для вычисления площади треугольника можно найти площадь треугольника в различных ситуациях, включая случаи, когда известны длины основания и высоты или все длины сторон треугольника.

Сумма углов треугольника

Для доказательства этого свойства можно воспользоваться различными способами. Один из них — построение параллельных прямых. Если провести параллельные прямые к двум сторонам треугольника, то получится два параллельных пересекающихся отрезка, которые образуют некоторый угол. Этот угол называется фактически внутренним углом треугольника. Если сложить все внутренние углы треугольника, то получится 180 градусов.

Другой способ доказательства состоит в использовании свойства параллельных прямых, которое гласит, что когда прямая пересекает две параллельные прямые, то все внутренние углы, образуемые пересекаемыми прямыми, равны между собой. Проведя параллельные прямые к двум сторонам треугольника, мы получим два параллельных пересекающихся отрезка, которые образуют некоторые углы. Поскольку эти углы равны, то и сумма всех внутренних углов треугольника равна 180 градусам.

Сумма углов треугольника — это важное геометрическое свойство, которое помогает в решении различных задач и построении различных фигур.

Треугольная неравенство

Формально, для треугольника с сторонами a, b и c, треугольное неравенство записывается следующим образом:

a + b > c

a + c > b

b + c > a

Если хотя бы одно из этих неравенств не выполняется, то треугольник с такими сторонами не может существовать.

Треугольная неравенство является важным инструментом в геометрии и находит применение в различных задачах, например, при доказательстве существования треугольника или при определении его типа (остроугольный, прямоугольный или тупоугольный).

Теорема Пифагора

Согласно теореме Пифагора, в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Формула теоремы Пифагора выглядит следующим образом:

c2 = a2 + b2

где c — гипотенуза, а a и b — катеты треугольника.

Теорема Пифагора позволяет найти длину одной из сторон треугольника, если известны длины двух других сторон. Она является основой для решения множества задач в геометрии и физике.

Вопрос-ответ:

Что такое треугольник в математике?

Треугольник — это геометрическая фигура, состоящая из трех отрезков, соединяющих три точки, которые не лежат на одной прямой.

Какие свойства имеет треугольник?

Треугольник имеет несколько основных свойств. Например, сумма внутренних углов треугольника равна 180 градусам. Также, длины сторон треугольника могут быть разными, но сумма любых двух сторон всегда больше третьей стороны.

Какие виды треугольников существуют?

В математике существует несколько видов треугольников. Например, треугольник может быть равносторонним, если все его стороны равны. Треугольник может быть равнобедренным, если две его стороны равны. Также существуют прямоугольные треугольники, у которых один из углов равен 90 градусам.

Как найти площадь треугольника?

Для нахождения площади треугольника можно использовать формулу Герона. Для этого необходимо знать длины его сторон. Площадь треугольника равна квадратному корню из произведения полупериметра треугольника и разности полупериметра и длины каждой из его сторон.

Какие формулы можно использовать для нахождения длин сторон треугольника?

Существует несколько формул, позволяющих найти длины сторон треугольника. Например, для прямоугольного треугольника можно использовать теорему Пифагора. Для равнобедренного треугольника можно использовать формулу для нахождения высоты. Для общего треугольника можно использовать теорему косинусов или теорему синусов.

Тригонометрические функции треугольника

Основными тригонометрическими функциями треугольника являются:

ФункцияОбозначениеОпределение

Синус	sin	Отношение противолежащего катета к гипотенузе
Косинус	cos	Отношение прилежащего катета к гипотенузе
Тангенс	tan	Отношение противолежащего катета к прилежащему катету
Котангенс	cot	Обратное значение тангенсу

Тригонометрические функции позволяют вычислить значения углов треугольника, а также находить длины сторон треугольника при известных значениях углов и одной из сторон. Они играют важную роль в решении геометрических задач и построении математических моделей в различных областях науки.

Видео по теме: