Математика пределы как решать

Узнайте, как решать задачи по нахождению пределов в математике. Получите подробные инструкции и примеры решения, а также узнайте основные правила и приемы, которые помогут вам успешно решить задачу по нахождению предела функции.

Математика – один из самых важных предметов в школе, который требует от учеников глубокого понимания и умения решать различные задачи. Одна из наиболее сложных тем в математике – это пределы. Понимание пределов позволяет решать задачи, связанные с приближением значений функций в бесконечно малой окрестности точки. В данной статье мы рассмотрим детальное объяснение и примеры, которые помогут вам научиться решать задачи по математике пределы.

Одной из основных концепций в пределах является понятие бесконечно малой последовательности. Бесконечно малая последовательность – это последовательность чисел, которая стремится к нулю приближаясь к бесконечности. Используя эту концепцию, можно определить предел функции. Предел функции показывает, к какому значению приближается функция при приближении аргумента к некоторому значению или бесконечности.

Пример: Рассмотрим функцию f(x) = 2x + 1. Если аргумент x приближается к значению 3, то значение функции f(x) будет приближаться к 7. То есть предел функции f(x) при x, стремящемся к 3, равен 7.

Для решения задач по пределам необходимо знать основные свойства пределов функций. Одно из таких свойств – это свойство суммы пределов. Если пределы функций f(x) и g(x) существуют при приближении аргумента к некоторому значению a, то предел функции суммы f(x) + g(x) будет равен сумме пределов функций f(x) и g(x).

Другое важное свойство пределов – это свойство произведения. Если пределы функций f(x) и g(x) существуют при приближении аргумента к некоторому значению a, то предел функции произведения f(x) * g(x) будет равен произведению пределов функций f(x) и g(x).

Определение предела функции

Пусть дана функция f(x) и точка a на числовой прямой. Говорят, что предел функции f(x) при x стремящемся к a равен числу L, если для любого положительного числа ε существует положительное число δ, такое что для всех x, отличных от a, удовлетворяющих условию 0 < |x — a| < δ, выполняется неравенство |f(x) — L| < ε.

Это определение можно переформулировать следующим образом: предел функции существует, если при достаточно малых значениях аргумента функция принимает значения, близкие к заданному числу L.

Если предел функции существует, то его значение не зависит от значения функции в самой точке a. Если предел не существует, то говорят, что функция не имеет предела в точке a.

Определение предела функции играет важную роль в различных областях математики и науки, таких как дифференциальное и интегральное исчисление, физика, экономика и другие.

Видео по теме:

Как найти предел функции аналитически

Для нахождения предела функции аналитически необходимо использовать алгебраические методы и свойства пределов. Это позволяет найти точное значение предела функции без необходимости использовать численные методы.

Основной шаг для нахождения предела функции аналитически — это приведение функции к виду, в котором можно легко вычислить пределы. Для этого можно использовать различные алгебраические преобразования, такие как раскрытие скобок, сокращение дробей, факторизация и т.д.

После приведения функции к удобному виду можно использовать свойства пределов функций, такие как арифметические свойства (сумма, разность, произведение, частное), свойства монотонности (пределы монотонной функции), свойства ограниченности (предел ограниченной функции) и другие.

Для более сложных функций может потребоваться применение специальных методов, таких как правило Лопиталя, использование тригонометрических тождеств, замена переменной и другие.

Важно помнить о граничных условиях и ограничениях на значения переменных, так как они могут влиять на предел функции. Также следует учитывать, что предел может быть равен бесконечности или не существовать в некоторых случаях.

Найденный аналитически предел функции позволяет узнать поведение функции вблизи данной точки, что может быть полезно при решении задач и анализе функций.

Предельные свойства функций

Основные предельные свойства функций включают:

1. Предел суммы: Если пределы функций f(x) и g(x) при x стремящемся к a существуют, то предел их суммы равен сумме пределов: lim(f(x) + g(x)) = lim(f(x)) + lim(g(x)).
2. Предел произведения: Если пределы функций f(x) и g(x) при x стремящемся к a существуют, то предел их произведения равен произведению пределов: lim(f(x) * g(x)) = lim(f(x)) * lim(g(x)).
3. Предел отношения: Если пределы функций f(x) и g(x) при x стремящемся к a существуют, и предел g(x) не равен нулю, то предел их отношения равен отношению пределов: lim(f(x) / g(x)) = lim(f(x)) / lim(g(x)).
4. Предел композиции: Если предел функции g(x) при x стремящемся к a равен b, а предел функции f(x) при x стремящемся к b существует, то предел их композиции равен пределу f(x) при x стремящемся к b: lim(f(g(x))) = lim(f(x)).

Эти предельные свойства играют важную роль в анализе и позволяют решать сложные задачи, связанные с определением пределов функций.

Вопрос-ответ:

Что такое предел функции?

Предел функции — это значение, к которому приближается функция, когда ее аргумент стремится к некоторому числу. Формально, если функция f(x) приближается к числу L, когда x стремится к числу a, то говорят, что предел функции равен L и записывается как lim f(x) = L при x → a.

Какой смысл имеет предел функции?

Предел функции позволяет понять, как функция ведет себя близко к определенной точке. Он позволяет вычислить значение функции в точке, которая может быть недоступна для вычислений напрямую. Предел также позволяет определить особенности функции, такие как разрывы и асимптоты.

Как решать задачи по пределам?

Для решения задач по пределам можно использовать различные методы, включая прямое вычисление, арифметические свойства пределов, замены переменной, использование известных пределов и использование теорем о пределах. Важно знать базовые правила и методы вычисления пределов, а также практиковаться в решении задач.

Какие арифметические операции можно применять при вычислении пределов?

При вычислении пределов можно применять арифметические операции, такие как сложение, вычитание, умножение и деление функций. Если пределы функций существуют, то пределы суммы, разности, произведения и частного этих функций также существуют и могут быть вычислены с использованием соответствующих правил.

Можно ли использовать графическое представление функции для решения задач по пределам?

Да, графическое представление функции может быть полезным инструментом для решения задач по пределам. График позволяет визуализировать поведение функции вблизи определенной точки и понять, какой предел у функции в этой точке. Графический метод также может помочь обнаружить особенности функции, такие как разрывы, асимптоты и экстремумы.

Таблица пределов основных функций

Для решения задач по математике, связанных с пределами, важно быть знакомым с таблицей пределов основных функций. Таблица представляет собой список наиболее часто встречающихся функций и их предельных значений.

Ниже приведена таблица пределов основных функций:

ФункцияПредел

константа $c$	$\lim\limits_{x \to a} c = c$
единичная функция $x$	$\lim\limits_{x \to a} x = a$
степенная функция $x^n$	$\lim\limits_{x \to a} x^n = a^n$
экспоненциальная функция $e^x$	$\lim\limits_{x \to \infty} e^x = \infty$
логарифмическая функция $\log_a{x}$	$\lim\limits_{x \to 0^+} \log_a{x} = -\infty$
тригонометрическая функция $\sin{x}$	$\lim\limits_{x \to 0} \sin{x} = 0$
обратная тригонометрическая функция $\arcsin{x}$	$\lim\limits_{x \to 0} \arcsin{x} = 0$

Зная эти пределы, вы сможете более эффективно решать задачи, связанные с определением предельного значения функции.

Примечание: В таблице приведены только некоторые основные функции и их предельные значения. Существует много других функций и их пределов, которые также могут быть полезны при решении задач по математике.

Логарифмические и тригонометрические функции

Логарифмические функции определяются через основание логарифма и аргумент. Они обратны экспоненциальным функциям и позволяют решать уравнения, связанные с изменением величин с течением времени или пространства. Основными свойствами логарифмических функций являются:

• Логарифм от произведения двух чисел равен сумме логарифмов от этих чисел: $\log(ab) = \log(a) + \log(b)$
• Логарифм от деления двух чисел равен разности логарифмов от этих чисел: $\log\left(\frac{a}{b}
  ight) = \log(a) — \log(b)$
• Логарифм от возведения числа в степень равен произведению степени и логарифма числа: $\log(a^b) = b \cdot \log(a)$

Тригонометрические функции определяются через угол и позволяют изучать связь между сторонами и углами в треугольниках. Они широко используются в физике, инженерии и других областях науки и техники. Основными свойствами тригонометрических функций являются:

• Синус угла равен отношению противолежащего катета к гипотенузе: $\sin(\theta) = \frac{opposite}{hypotenuse}$
• Косинус угла равен отношению прилежащего катета к гипотенузе: $\cos(\theta) = \frac{adjacent}{hypotenuse}$
• Тангенс угла равен отношению противолежащего катета к прилежащему катету: $\tan(\theta) = \frac{opposite}{adjacent}$

Знание этих свойств и правил работы с логарифмическими и тригонометрическими функциями поможет вам успешно решать задачи по пределам и использовать их в других областях математики и наук.

Примеры решения задач по математике пределы

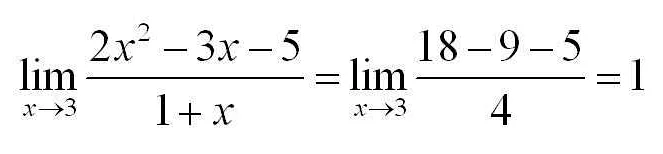
Рассмотрим несколько примеров решения задач по математике, связанных с пределами функций.

1. Пример 1:

   Найти предел функции f(x) = 2x + 3 при x стремящемся к 4.

   Решение:

   Для нахождения предела данной функции, необходимо подставить значение предела вместо переменной x и вычислить значение функции.

   Подставим x = 4 в функцию:

   f(4) = 2(4) + 3 = 11

   Таким образом, предел функции f(x) = 2x + 3 при x стремящемся к 4 равен 11.

2. Пример 2:

   Найти предел функции f(x) = (x^2 — 1)/(x — 1) при x стремящемся к 1.

   Решение:

   Для нахождения предела данной функции, можно воспользоваться алгебраическими преобразованиями, чтобы устранить неопределенность вида 0/0.

   Разложим числитель по формуле разности квадратов:

   f(x) = [(x — 1)(x + 1)]/(x — 1)

   Сократим (x — 1) в числителе и затем подставим x = 1:

   f(1) = x + 1 = 2

   Таким образом, предел функции f(x) = (x^2 — 1)/(x — 1) при x стремящемся к 1 равен 2.

3. Пример 3:

   Найти предел функции f(x) = sin(x)/x при x стремящемся к 0.

   Решение:

   Для нахождения предела данной функции, можно воспользоваться тригонометрическим соотношением:

   lim(sin(x)/x) = 1

   Таким образом, предел функции f(x) = sin(x)/x при x стремящемся к 0 равен 1.

В этих примерах продемонстрировано, как можно находить пределы функций при различных значениях переменных. Решая подобные задачи, можно лучше разобраться с понятием предела и его применением в математике.

Трюки при решении задач по пределам

1. Применение арифметических свойств пределов:

При решении задач по пределам можно использовать арифметические свойства пределов, такие как сумма, разность, произведение и частное пределов. Это позволяет сократить выражение и упростить его вычисление.

2. Применение замечательных пределов:

Замечательные пределы – это пределы, которые можно выразить в явном виде и использовать при решении задач. Например, пределы вида lim(x -> 0) (sin(x) / x) = 1 и lim(x -> ∞) (1 + 1/x)^x = e являются замечательными пределами и часто встречаются в задачах.

3. Использование замены переменной:

При решении сложных задач по пределам можно использовать замену переменной. Замена переменной может сделать выражение более простым и позволить легче найти предел.

4. Применение правила Лопиталя:

Правило Лопиталя позволяет находить пределы некоторых функций, которые оказываются неопределенными вида 0/0 или ∞/∞. С помощью правила Лопиталя можно заменить функцию на ее производную и продолжить вычисление предела.

5. Использование геометрического смысла предела:

Геометрический смысл предела позволяет визуализировать процесс стремления переменной к определенному значению. Это может помочь понять, какие значения переменной следует рассматривать при вычислении предела и каким образом он стремится к этому значению.

6. Разложение функции в ряд Тейлора:

При решении некоторых сложных задач по пределам можно использовать разложение функции в ряд Тейлора. Ряд Тейлора позволяет приближенно выразить функцию в виде бесконечной суммы слагаемых, что облегчает вычисление предела.

Использование этих трюков и методов позволяет более эффективно и точно решать задачи по пределам. Однако, важно помнить, что такие трюки следует применять с осторожностью и всегда проверять результаты вычислений.

Проверка правильности решения задач по пределам

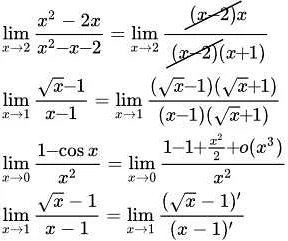
После того, как вы решили задачу по пределам, важно проверить правильность своего решения. Это поможет вам убедиться, что вы не допустили ошибок и получили правильный ответ.

Для проверки решения задачи по пределам можно использовать несколько методов. Вот некоторые из них:

МетодОписание

Аналитический метод	Этот метод заключается в анализе алгебраических и арифметических операций, проведенных в ходе решения, и вычислении предела по определению. Если все операции выполнены правильно и предел вычислен верно, то решение считается правильным.
Графический метод	В этом методе необходимо построить график функции, представленной в задаче, и визуально оценить поведение функции в окрестности точки предела. Если график подтверждает полученный ответ, то решение считается правильным.
Численный метод	В этом методе предлагается вычислить значение функции для нескольких значений, стремящихся к точке предела, и сравнить полученные результаты. Если все значения приближаются к одному и тому же числу, то решение считается правильным.

Важно помнить, что при проверке решения задач по пределам необходимо учитывать все условия, указанные в задаче, и следовать математическим правилам и свойствам пределов. Также рекомендуется использовать калькулятор или программное обеспечение для вычисления сложных арифметических операций.

Если вы обнаружили ошибку в своем решении, необходимо вернуться к задаче и перепроверить каждый шаг решения. Также можно обратиться к учебнику или преподавателю за помощью.