Что такое верный корень в математике

Верный корень в математике – это значение, которое при возведении в заданную степень даёт исходное число. Узнайте, как найти верный корень и как он применяется в различных математических задачах.

Верный корень — это математическое понятие, которое используется для нахождения решений квадратных уравнений и корней других степеней. Он представляет собой число, возведенное в степень, которая дает исходное число.

Для примера, квадратный корень из числа 9 равен 3, потому что 3 в квадрате равно 9. Таким образом, 3 является верным корнем числа 9. Верные корни могут быть положительными и отрицательными, так как квадраты чисел могут быть как положительными, так и отрицательными.

Верные корни широко используются в различных областях математики, физики, инженерии и других науках. Они позволяют решать уравнения, моделировать физические явления и проводить точные расчеты.

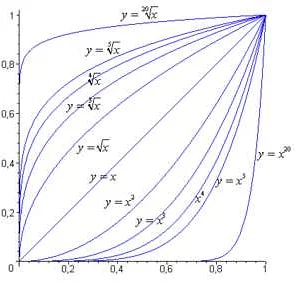
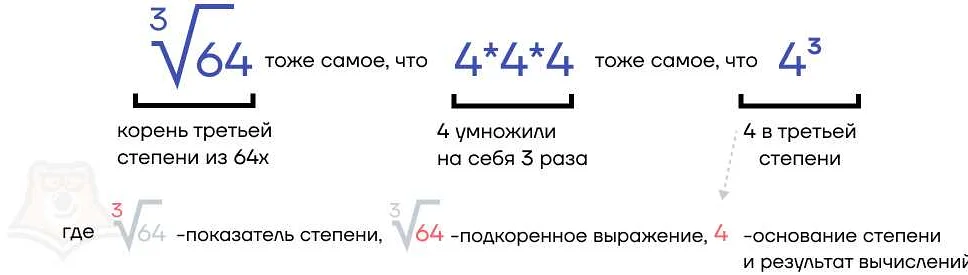
В математике используется специальный символ для обозначения верного корня — радикал. Например, корень из числа 16 записывается как √16. Верный корень может быть выражен как рациональное или иррациональное число, в зависимости от того, можно ли его представить в виде отношения двух целых чисел.

Верные корни могут быть использованы для решения различных задач, таких как нахождение длины стороны квадрата или прямоугольника, определение времени падения объекта или расчет электрического сопротивления. Они также применяются в финансовой математике для расчета процентной ставки и дисконтирования будущих денежных потоков. Понимание верных корней является важным элементом для успешного решения таких задач.

Что такое верный корень в математике?

Чтобы найти верный корень, необходимо найти число, которое при возведении в квадрат даст исходное число. Например, корень из 9 равен 3, потому что 3^2 = 9.

Верный корень может быть извлечен из любого положительного числа, но не из отрицательного числа. Если число отрицательное, то верный корень будет комплексным числом.

Кроме того, верный корень может быть извлечен не только из целых чисел, но и из десятичных дробей. Например, корень из 2 равен примерно 1,4142.

Верный корень играет важную роль в математике и находит свое применение во многих областях, включая физику, инженерию и экономику.

Примеры расчета верного корня:

1. Корень из 16 равен 4, потому что 4^2 = 16.
2. Корень из 25 равен 5, потому что 5^2 = 25.
3. Корень из 36 равен 6, потому что 6^2 = 36.

Определение и свойства

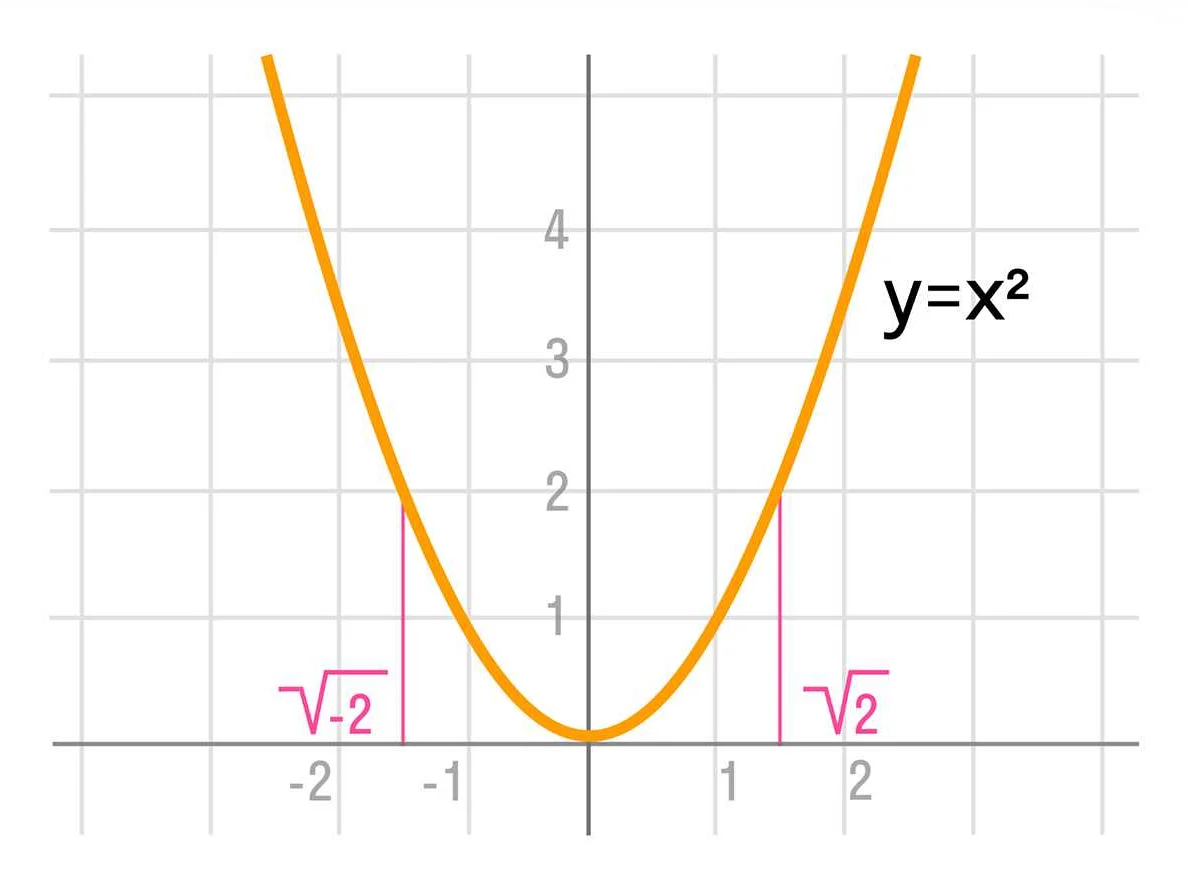
Для примера, рассмотрим уравнение x2 — 4 = 0. В данном случае, верными корнями будут числа, которые при подстановке вместо x приведут к верному равенству. В данном случае, верными корнями будут числа 2 и -2, так как 22 — 4 = 4 — 4 = 0 и (-2)2 — 4 = 4 — 4 = 0.

Основные свойства верных корней:

1. Уравнение может иметь один или более верных корней.
2. Каждый верный корень возводящего в него уравнения является решением этого уравнения.
3. Если уравнение имеет верный корень, то оно является многочленом.
4. Некоторые уравнения могут иметь только комплексные верные корни.

Определение и свойства верных корней являются важными понятиями в математике, и используются в различных областях, таких как алгебра, анализ, физика и технические науки.

Расчеты с верным корнем

Расчеты с верным корнем часто применяются для решения уравнений. Например, рассмотрим простое уравнение:

x^2 — 4x + 3 = 0

Для нахождения верных корней этого уравнения можно воспользоваться формулой дискриминанта:

D = b^2 — 4ac

где a, b и c — коэффициенты уравнения. В данном случае a = 1, b = -4 и c = 3.

Подставим значения коэффициентов в формулу:

D = (-4)^2 — 4 * 1 * 3 = 16 — 12 = 4

Извлекая квадратный корень из дискриминанта, получаем:

√D = √4 = ±2

Таким образом, уравнение имеет два верных корня:

x1 = (-b — √D) / (2a) = (-(-4) — 2) / (2 * 1) = (4 — 2) / 2 = 2 / 2 = 1

x2 = (-b + √D) / (2a) = (-(-4) + 2) / (2 * 1) = (4 + 2) / 2 = 6 / 2 = 3

Таким образом, верными корнями данного уравнения являются x1 = 1 и x2 = 3.

Расчеты с верным корнем позволяют найти значения переменных, при которых уравнение выполняется и оказывается верным. Это полезный инструмент в математике, который позволяет решать различные задачи и находить точные значения переменных.

Примеры задач

Рассмотрим несколько примеров задач, в которых при расчетах используется понятие верного корня.

Пример 1:

Найдите верный корень уравнения: x2 — 3x + 2 = 0.

Решение:

Для нахождения верного корня уравнения, нужно решить квадратное уравнение для x.

Вычислим дискриминант: D = b2 — 4ac.

В нашем случае: a = 1, b = -3, c = 2.

Тогда: D = (-3)2 — 4 * 1 * 2 = 9 — 8 = 1.

Так как дискриминант равен положительному числу, у уравнения есть два верных корня.

Найдем верные корни уравнения, используя формулу: x = (-b ± √D) / (2a).

Подставим значения: x1 = (-(-3) + √1) / (2 * 1) = (3 + 1) / 2 = 4 / 2 = 2.

Таким образом, верный корень уравнения x2 — 3x + 2 = 0 равен 2.

Теперь найдем второй верный корень:

x2 = (-(-3) — √1) / (2 * 1) = (3 — 1) / 2 = 2 / 2 = 1.

Итак, уравнение x2 — 3x + 2 = 0 имеет два верных корня: 2 и 1.

Пример 2:

Вычислите верный корень выражения: √(9 + 16).

Решение:

Сначала произведем вычисление внутреннего выражения: 9 + 16 = 25.

Затем возьмем корень из получившегося числа: √25 = 5.

Таким образом, верный корень выражения √(9 + 16) равен 5.

Пример 3:

Решите уравнение: 2x + 3 = 11.

Решение:

Перенесем число 3 на другую сторону уравнения:

2x = 11 — 3 = 8.

Далее разделим обе части уравнения на 2:

x = 8 / 2 = 4.

Таким образом, верный корень уравнения 2x + 3 = 11 равен 4.

Алгоритм нахождения верного корня

Для нахождения верного корня можно использовать различные алгоритмы, в зависимости от типа уравнения или системы уравнений. Один из таких алгоритмов — это метод итераций.

Метод итераций основан на принципе последовательного приближения к верному корню. Алгоритм состоит из следующих шагов:

1. Выбрать начальное приближение верного корня.
2. Подставить это приближение в уравнение или систему уравнений.
3. Вычислить значение функции или системы уравнений для данного приближения.
4. Если значение функции или системы уравнений близко к нулю, то текущее приближение является верным корнем. Процесс останавливается.
5. Если значение функции или системы уравнений не равно нулю, то текущее приближение не является верным корнем. Переход к следующему шагу.
6. Использовать полученное значение функции или системы уравнений для уточнения приближения к верному корню.
7. Вернуться к шагу 2 и повторить процесс до достижения заданной точности или достижения верного корня.

Примером применения алгоритма нахождения верного корня может служить решение уравнения x^2 — 4 = 0. Начальное приближение верного корня можно выбрать, например, равным 2. Подставив это значение в уравнение, получим 2^2 — 4 = 0. Результат равен нулю, что означает, что текущее приближение является верным корнем. Процесс останавливается.

Алгоритм нахождения верного корня является важным инструментом для решения различных математических задач. Его применение позволяет найти значения переменных, которые удовлетворяют уравнениям и системам уравнений, и таким образом решить поставленные задачи.

Более сложные примеры расчетов

Верный корень в математике используется для нахождения числа, которое возведенное в квадрат дает исходное число. При решении более сложных примеров с использованием верного корня, необходимо учитывать особенности выражений и правила их преобразования.

Рассмотрим пример: найти верный корень уравнения x2 + 4x — 12 = 0. Для этого нужно привести уравнение к квадратному виду и применить формулу дискриминанта.

Перенесем все слагаемые в левую часть уравнения: x2 + 4x — 12 = 0. Получим x2 + 4x — 12 = 0.

Применим формулу дискриминанта: D = b2 — 4ac, где a = 1, b = 4, c = -12.

Вычисляем: D = 42 — 4 * 1 * (-12) = 16 + 48 = 64.

Если D > 0, то уравнение имеет два корня. Вычисляем корни по формуле: x1,2 = (-b ± √D) / 2a.

Подставляем значения: x1,2 = (-4 ± √64) / 2 * 1.

Вычисляем: x1 = (-4 + 8) / 2 = 4 / 2 = 2 и x2 = (-4 — 8) / 2 = -12 / 2 = -6.

Таким образом, верные корни уравнения x2 + 4x — 12 = 0 равны 2 и -6.

В более сложных примерах расчетов с использованием верного корня может потребоваться применение различных методов и формул. Важно правильно анализировать задачу и применять соответствующие математические приемы для ее решения.

Вопрос-ответ:

Что такое верный корень в математике?

Верный корень в математике — это число, которое при возведении в заданную степень даёт исходное число.

Можете привести примеры верных корней?

Конечно! Например, корень квадратный из 9 равен 3, так как 3 * 3 = 9. Или корень кубический из 8 равен 2, так как 2 * 2 * 2 = 8.

Какие виды корней существуют в математике?

В математике существуют различные виды корней, включая квадратный корень, кубический корень, корень с любой другой четной степенью и корень с отрицательным показателем степени.

Как найти верный корень из числа?

Для нахождения верного корня из числа нужно найти число, возведенное в заданную степень, которое будет равно исходному числу. Для этого можно использовать специальные математические операции и формулы.

Зачем нужно знать понятие верного корня в математике?

Знание понятия верного корня в математике позволяет решать различные задачи и проблемы, связанные с вычислениями, а также упрощает работу с математическими формулами и уравнениями.

Значение верного корня в практическом применении

Одним из примеров практического применения верного корня является решение квадратного уравнения. Например, уравнение x^2 — 4x + 3 = 0 имеет два верных корня: x = 1 и x = 3. Подставляя эти значения в уравнение, мы получаем:

При x = 1:

1^2 — 4 * 1 + 3 = 1 — 4 + 3 = 0

При x = 3:

3^2 — 4 * 3 + 3 = 9 — 12 + 3 = 0

Таким образом, значения x = 1 и x = 3 являются верными корнями квадратного уравнения.

Верные корни также широко используются в физике, инженерии и других областях науки. Например, при решении задач по механике, электричеству и другим физическим явлениям, верные корни позволяют определить значения физических величин. Кроме того, они используются при моделировании и прогнозировании различных процессов и явлений.

Верные корни также могут быть использованы для проверки правильности решений уравнений и систем уравнений. Подстановка верных корней в уравнение или систему уравнений должна давать равенство, что позволяет убедиться в правильности найденного решения.

Таким образом, понимание и использование верных корней в практическом применении позволяет решать уравнения, определять значения переменных и проводить проверку правильности решений.

Видео по теме: