Что относится к математическому моделированию
Содержимое
- 1 Что относится к математическому моделированию
- 1.1 Значение математического моделирования
- 1.2 Видео по теме:
- 1.3 Важность математического моделирования в науке и технике
- 1.4 Основные принципы математического моделирования
- 1.5 Методы математического моделирования
- 1.6 Примеры применения математического моделирования
- 1.7 Вычислительные алгоритмы в математическом моделировании
- 1.8 Основные сложности и ограничения математического моделирования
- 1.9 Преимущества и недостатки математического моделирования
- 1.10 Вопрос-ответ:
- 1.10.0.1 Какие основные аспекты включает в себя математическое моделирование?
- 1.10.0.2 Какие шаги включает в себя процесс математического моделирования?
- 1.10.0.3 Зачем нужно математическое моделирование?
- 1.10.0.4 Какие примеры применения математического моделирования в разных областях?
- 1.10.0.5 Какие инструменты и методы применяются в математическом моделировании?
- 1.10.0.6 Что такое математическое моделирование?
Математическое моделирование включает в себя использование математических методов и инструментов для создания абстрактных моделей реальных систем и процессов. В данной статье рассматривается, что относится к математическому моделированию и какие применяются методы для решения различных задач и прогнозирования будущих событий.
Математическое моделирование — это процесс создания математической модели, которая описывает реальный объект или систему. Основная цель математического моделирования заключается в получении количественного описания явлений, процессов и взаимодействий в реальном мире.
В процессе математического моделирования важную роль играют основные аспекты, которые необходимо учесть. Во-первых, необходимо определить, какие явления и процессы необходимо учесть при создании модели. Во-вторых, необходимо выбрать математические методы и инструменты для описания этих явлений и процессов. В-третьих, необходимо провести верификацию и валидацию модели, чтобы убедиться в ее точности и соответствии реальным данным.
Математическое моделирование находит применение в различных областях науки и техники, таких как физика, химия, экономика, биология, инженерия и другие. С помощью математического моделирования ученые и исследователи могут анализировать сложные системы, прогнозировать их поведение, оптимизировать процессы и принимать взвешенные решения на основе полученных результатов.
Важно отметить, что математическое моделирование не является абсолютной истиной, а лишь приближенным описанием реальности. Ошибки и неточности могут возникать как при создании модели, так и при сборе и анализе данных. Поэтому важным аспектом математического моделирования является критическое отношение к результатам и постоянное совершенствование моделей на основе новых данных и открытий.
Значение математического моделирования
Одним из основных аспектов математического моделирования является возможность предсказывать поведение и свойства объектов или явлений на основе этих моделей. Математические модели позволяют анализировать и понимать различные процессы, оптимизировать решения, прогнозировать развитие событий и оценивать риски.
Математическое моделирование также помогает упростить сложные задачи и процессы, а также исследовать их в различных условиях и вариантах. Оно позволяет проводить численные эксперименты, которые могут быть невозможны или слишком дорогостоящими в реальности.
Кроме того, математическое моделирование способствует разработке новых теорий, методов и алгоритмов. Оно помогает находить оптимальные решения в различных задачах и принимать обоснованные решения на основе количественного анализа и оценки.
Таким образом, математическое моделирование является неотъемлемой частью современной науки и техники. Оно помогает углубить наше понимание мира, предсказать его возможное развитие и принять обоснованные решения в различных областях деятельности.
Видео по теме:
Важность математического моделирования в науке и технике
Одним из основных аспектов математического моделирования является возможность предсказания поведения системы или процесса в различных условиях. Это позволяет исследователям и инженерам прогнозировать результаты экспериментов и оптимизировать процессы.
Математическое моделирование также позволяет проводить виртуальные эксперименты, которые могут быть слишком опасными, дорогостоящими или времязатратными в реальности. Например, при проектировании новых автомобилей или самолетов, математические модели позволяют проверять их характеристики и безопасность до того, как они будут построены и испытаны в реальных условиях.
Благодаря математическому моделированию, исследователи и инженеры могут также оптимизировать системы и процессы, чтобы достичь оптимальных результатов. Например, в производстве товаров или услуг, математические модели могут помочь определить оптимальные параметры процессов и распределение ресурсов, что в конечном итоге может привести к снижению затрат и повышению эффективности.
Кроме того, математическое моделирование позволяет исследователям и инженерам изучать сложные и непредсказуемые системы, такие как погода, климатические изменения или распространение эпидемий. Моделирование помогает анализировать и понимать эти системы, что может быть полезным для прогнозирования и разработки стратегий управления.
Таким образом, математическое моделирование играет критическую роль в науке и технике, обеспечивая возможность прогнозирования, оптимизации и анализа различных систем и процессов. Оно помогает исследователям и инженерам принимать обоснованные решения, сокращать расходы и улучшать качество жизни людей.
Основные принципы математического моделирования
- Упрощение и абстракция: Для создания математической модели необходимо упростить сложность реальной системы, выделить наиболее важные аспекты и абстрагироваться от незначительных деталей.
- Формализация: Математическая модель должна быть выражена с помощью формального языка, такого как алгебраические уравнения, дифференциальные уравнения или стохастические процессы.
- Валидация: Проверка математической модели на соответствие реальным данным и явлениям. Валидация позволяет убедиться, что модель действительно описывает систему или явление и может быть использована для прогнозирования.
- Адаптация и оптимизация: В процессе математического моделирования модель может быть изменена и уточнена на основе новых данных и наблюдений. Также может производиться оптимизация модели с целью достижения наилучших результатов.
- Интерпретация и практическое применение: Результаты математического моделирования должны быть интерпретированы и применены на практике для решения конкретных задач, прогнозирования будущих событий или улучшения процессов.
Основные принципы математического моделирования помогают ученым, инженерам и другим специалистам создавать эффективные модели, которые могут быть использованы для анализа и предсказания различных систем и явлений в науке, технике, экономике и других областях.
Методы математического моделирования

Математическое моделирование включает в себя различные методы и подходы, которые позволяют описывать и анализировать реальные явления и процессы с помощью математических моделей. Вот некоторые из основных методов математического моделирования:
- Аналитический метод — в основе этого метода лежит использование аналитического подхода к построению математической модели. Он основывается на математических законах и формулах, которые позволяют найти точные решения уравнений и описать явления с высокой точностью.
- Численный метод — этот метод основывается на использовании численных алгоритмов для приближенного решения математических моделей. С помощью численных методов можно анализировать сложные системы, которые не могут быть решены аналитически.
- Статистический метод — данный метод используется для моделирования случайных процессов и явлений. Он основывается на статистическом анализе данных и позволяет предсказывать вероятности различных событий.
- Оптимизационный метод — этот метод используется для нахождения оптимальных решений и оптимизации различных процессов. Он основывается на математических методах оптимизации и позволяет найти наилучшие решения с учетом заданных ограничений.
Каждый из этих методов имеет свои преимущества и недостатки и может быть применен в зависимости от конкретной задачи и требований моделирования. Важно выбрать подходящий метод и правильно применить его для достижения поставленных целей.
Примеры применения математического моделирования

Математическое моделирование находит широкое применение в различных областях науки, техники и бизнеса. Ниже приведены несколько примеров использования математического моделирования:
1. Физика: Математическое моделирование позволяет предсказывать поведение физических систем, таких как движение тел, электромагнитные поля и теплопередача. Оно используется для разработки новых технологий и оптимизации существующих процессов.
2. Экономика: Математические модели используются для анализа экономических процессов, таких как рыночная конкуренция, потребительское поведение и инвестиционные стратегии. Они помогают прогнозировать экономические показатели и принимать обоснованные решения.
3. Медицина: Математическое моделирование применяется для изучения биологических систем, таких как динамика заболеваний и эффективность лекарственных препаратов. Оно помогает разрабатывать новые методы диагностики и лечения.
4. Инженерия: Математические модели используются для проектирования и оптимизации инженерных систем, таких как электрические сети, автомобили и самолеты. Они позволяют предсказывать поведение системы и улучшать ее характеристики.
5. Климатология: Математическое моделирование позволяет изучать климатические процессы и прогнозировать изменения в погоде и климате. Оно помогает улучшать понимание климатических явлений и принимать меры по адаптации к изменению климата.
Примеров применения математического моделирования гораздо больше, и это лишь некоторые из них. Оно играет важную роль в научном и техническом прогрессе, позволяя анализировать сложные системы и принимать обоснованные решения.
Вычислительные алгоритмы в математическом моделировании
Вычислительные алгоритмы играют важную роль в математическом моделировании. Они позволяют решать сложные задачи, связанные с моделированием реальных систем, анализом данных и прогнозированием результатов.
Одним из основных алгоритмов, используемых в математическом моделировании, является численное интегрирование. Этот алгоритм позволяет приближенно находить значение определенного интеграла, что особенно полезно при решении задач, в которых аналитическое решение неизвестно или трудно получить.
Другим важным алгоритмом является численное решение дифференциальных уравнений. Дифференциальные уравнения широко используются для описания динамики систем, и численное решение позволяет получить приближенное решение таких уравнений на заданном интервале времени.
В математическом моделировании также используются алгоритмы оптимизации. Они позволяют находить оптимальные значения параметров модели или функции, учитывая ограничения и целевую функцию. Алгоритмы оптимизации могут быть применены, например, для оптимизации расписания производства или для нахождения наилучшей стратегии управления.
Большое значение в математическом моделировании имеют также алгоритмы статистического анализа данных. Они позволяют находить закономерности и зависимости в данных, проводить статистические тесты гипотез, строить модели прогнозирования и анализировать риски.
Все эти вычислительные алгоритмы требуют правильного выбора методов и адекватной реализации. Кроме того, они требуют компьютерного программирования и использования специализированных программных средств. Все это делает вычислительные алгоритмы неотъемлемой частью математического моделирования.
Основные сложности и ограничения математического моделирования

Одной из основных сложностей является необходимость учета всех взаимосвязей и факторов, которые могут оказывать влияние на моделируемую систему. Реальные системы часто имеют сложную структуру и множество взаимодействующих элементов, что делает точное моделирование невозможным. Поэтому моделирующие математические модели должны быть упрощены, что может привести к потере части информации и некоторым неточностям.
Другой сложностью является необходимость определения и оценки значений параметров модели. В реальных системах могут быть неизвестные или неполные данные, что может затруднить процесс моделирования. Ошибки в определении параметров могут приводить к неточным результатам и неверным прогнозам.
Ограничения математического моделирования также связаны с ограничениями математических методов и алгоритмов. Некоторые модели могут быть слишком сложными для точного решения, а некоторые проблемы могут быть формализованы только частично. Кроме того, существуют проблемы с вычислительной сложностью и временем выполнения моделей, особенно в случае больших и сложных систем.
Все эти сложности и ограничения необходимо учитывать при математическом моделировании, чтобы получить адекватные результаты и прогнозы. Важно также учитывать, что моделирование — это упрощение реальности, и результаты моделирования всегда являются приближенными и предположительными.
Преимущества и недостатки математического моделирования

Преимущества математического моделирования:
- Позволяет исследовать системы, которые сложно или невозможно изучить в реальности.
- Позволяет проводить эксперименты в виртуальной среде, что экономит время и ресурсы.
- Позволяет предсказывать результаты и оптимизировать процессы.
- Позволяет делать прогнозы на будущее и принимать обоснованные решения.
- Позволяет проводить исследования и тестирования без риска для жизни и здоровья людей.
Недостатки математического моделирования:
- Моделирующая система может быть слишком упрощенной и не учитывать все факторы.
- Точность модели зависит от точности входных данных и параметров модели.
- Возможность ошибки в моделировании, особенно при сложных системах.
- Необходимость математических и программных навыков для создания и анализа моделей.
- Моделирующая система может быть неэффективной или затратной по времени и ресурсам.
В целом, математическое моделирование имеет множество преимуществ, но также сопровождается некоторыми недостатками. Поэтому, при использовании этого инструмента необходимо учитывать его ограничения и особенности для достижения максимальной точности и полезности.
Вопрос-ответ:
Какие основные аспекты включает в себя математическое моделирование?
Математическое моделирование включает в себя разработку математических моделей, описание и анализ системы, решение математической модели, интерпретацию результатов и их применение в практических задачах.
Какие шаги включает в себя процесс математического моделирования?
Процесс математического моделирования включает в себя следующие шаги: формулирование задачи, построение математической модели, решение модели, интерпретация результатов и проверка модели на соответствие реальности.
Зачем нужно математическое моделирование?
Математическое моделирование используется для исследования и анализа сложных систем, предсказания их поведения, принятия решений и оптимизации процессов. Оно позволяет упростить и изучить систему, а также предсказать ее будущее состояние.
Какие примеры применения математического моделирования в разных областях?
Математическое моделирование применяется в различных областях, например, в физике для описания движения тел, в экономике для моделирования рынков, в биологии для изучения популяций, в психологии для анализа человеческого поведения и т.д.
Какие инструменты и методы применяются в математическом моделировании?
В математическом моделировании используются различные инструменты и методы, такие как дифференциальные уравнения, статистические методы, оптимизация, численные методы, компьютерное моделирование и другие.
Что такое математическое моделирование?
Математическое моделирование — это процесс создания математической модели, которая описывает определенную систему или процесс. Математическая модель представляет собой абстрактную форму системы, в которой используются математические символы, уравнения и принципы, чтобы описать поведение и свойства системы.

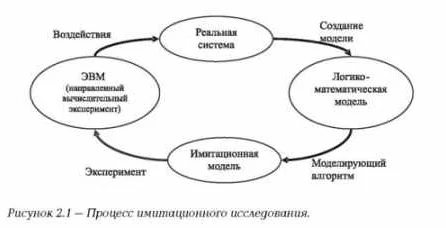
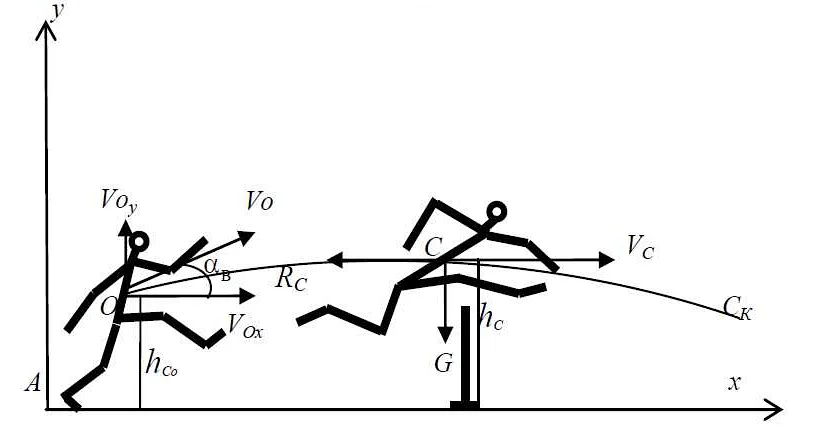

Математическое моделирование — это мощный инструмент, который позволяет нам понять и предсказывать различные явления и процессы в нашем мире. В основе математического моделирования лежит анализ и формализация реальных ситуаций с помощью математических методов и уравнений. Важными аспектами математического моделирования являются выбор и построение подходящей математической модели, а также ее верификация и валидация. Для этого необходимо учитывать различные факторы, такие как физические законы, параметры системы, начальные условия и граничные условия. Математическое моделирование может применяться в различных областях, таких как физика, биология, экономика, инженерия и другие. В физике, например, математическое моделирование позволяет предсказывать поведение физических систем, таких как движение тел или электромагнитные волны. В биологии оно может помочь исследовать динамику популяций или распространение заболеваний. Однако математическое моделирование имеет свои ограничения. Модель может быть только приближенной, и ее результаты зависят от точности исходных данных и использованных математических методов. Кроме того, модель может учитывать только определенные аспекты реальной ситуации, что может привести к упрощению искажению результатов. В целом, математическое моделирование — это мощный инструмент, который помогает нам понять и предсказывать сложные явления и процессы в нашем мире. Однако его результаты следует интерпретировать с осторожностью, учитывая его ограничения и приближенный характер.
Статья очень интересная и полезная! Математическое моделирование включает в себя множество аспектов, которые позволяют предсказывать и анализировать различные явления и процессы в нашей жизни. Благодаря математическим моделям мы можем понять, как работает мир вокруг нас и принимать обоснованные решения. Важно отметить, что математическое моделирование требует не только глубоких знаний математики, но и умения адаптироваться к различным условиям и ограничениям. Кроме того, оно также включает в себя работу с компьютерами и программами, которые помогают проводить сложные вычисления и визуализировать результаты моделирования. Основные аспекты математического моделирования включают выбор подходящей математической модели, сбор и анализ данных, проверку и верификацию модели, а также интерпретацию полученных результатов. В целом, математическое моделирование — это мощный инструмент, который позволяет нам лучше понимать мир вокруг нас и принимать обоснованные решения.
Математическое моделирование — это процесс создания абстрактной математической модели, которая позволяет описать и предсказать реальные явления или системы. Такие модели могут быть использованы в различных областях, включая физику, экономику, биологию и технику. Одним из основных аспектов математического моделирования является формулировка математических уравнений, которые описывают поведение системы. Эти уравнения могут быть дифференциальными, алгебраическими или комбинированными. Затем модель решается численно с использованием методов численного анализа. Полученные результаты могут быть использованы для анализа и оптимизации системы, а также для прогнозирования ее поведения в различных условиях. Важно отметить, что математическое моделирование — это лишь упрощенное представление реальной системы, и результаты моделирования всегда требуют проверки на эксперименте или наблюдении.