Что такое диагональ в математике

Диагональ в математике — это линия, соединяющая две несоседние вершины многоугольника или точки на прямой. Узнайте, как определить длину диагонали и использовать ее в геометрии и теории чисел.

Диагональ – это прямая линия, соединяющая две несоседние вершины многоугольника. В математике диагональ имеет особое значение и является одним из основных элементов геометрических фигур. Она позволяет нам изучать различные свойства и особенности многоугольников, а также применять их в решении разнообразных задач.

Диагонали обладают несколькими важными свойствами. Во-первых, они делят многоугольник на два треугольника или более. Во-вторых, диагонали могут быть равными или неравными. Неравные диагонали обычно пересекаются внутри многоугольника, в то время как равные диагонали могут быть параллельными или совпадать. В-третьих, длины диагоналей могут быть использованы для вычисления площади многоугольника и его периметра.

Например, в ромбе все четыре диагонали равны между собой и делят фигуру на четыре равных треугольника. В квадрате все диагонали равны, а в прямоугольнике с равными сторонами диагонали являются равными, а с противоположными сторонами — перпендикулярными. Диагонали треугольника и, в частности, медианы, могут использоваться для нахождения центра тяжести треугольника и построения его высот.

Изучение диагоналей многоугольников помогает понять их структуру, взаимосвязи между сторонами и углами, а также применять полученные знания для решения задач разной сложности. Это ключевой элемент геометрии, который находит свое применение в различных областях науки, техники и искусства.

Определение диагонали в математике

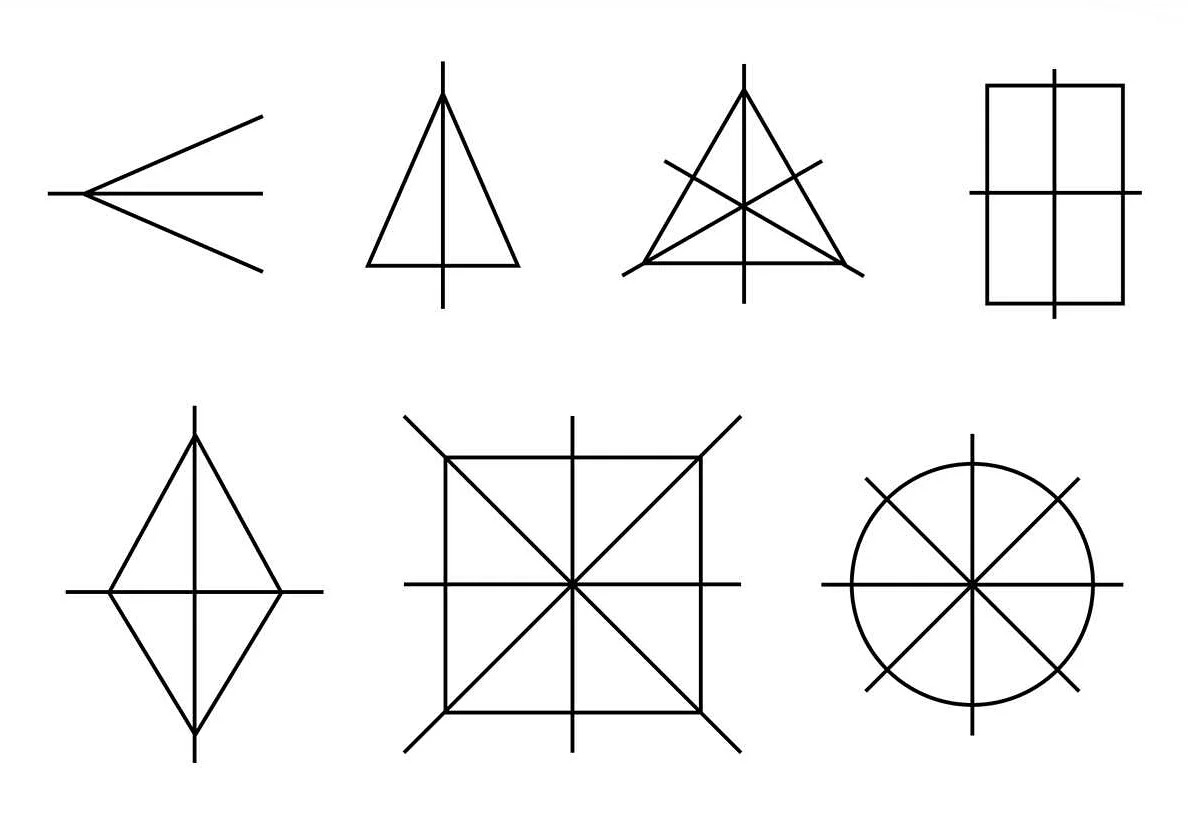
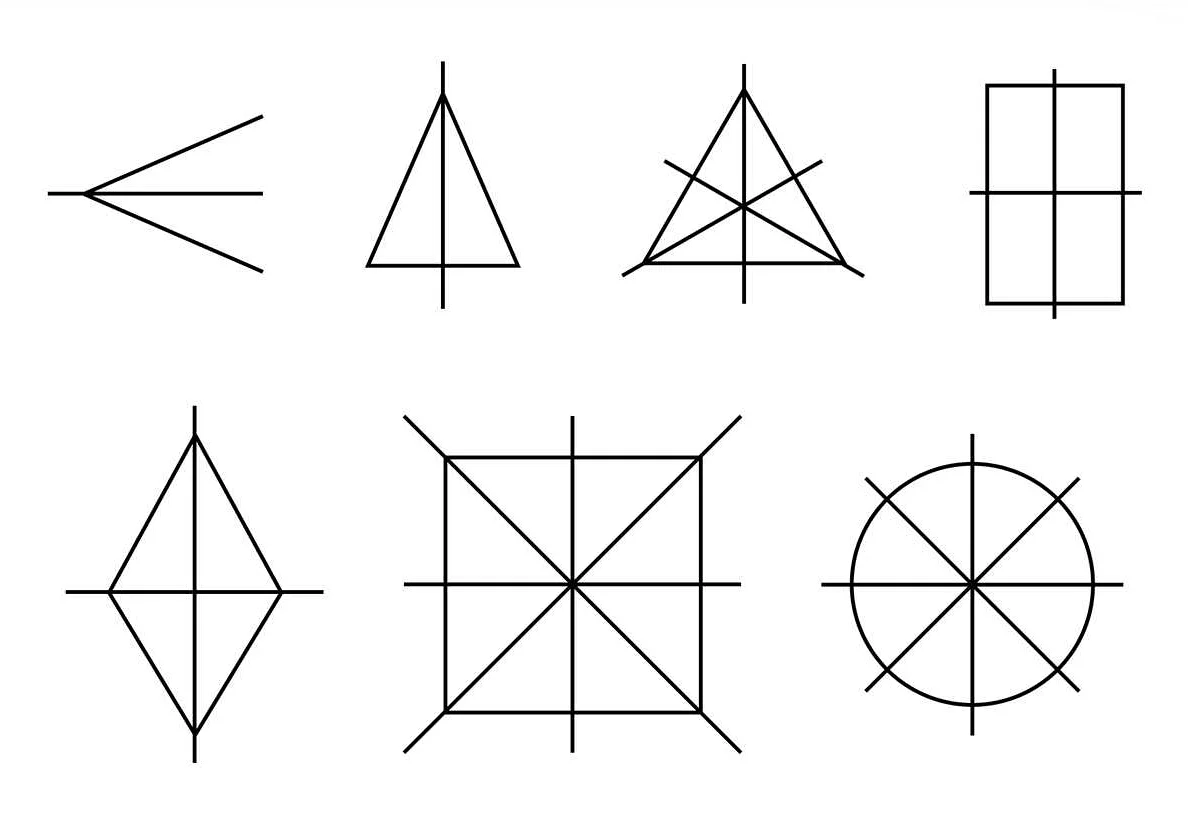
Диагональ может быть проведена в различных фигурах, таких как прямоугольник, квадрат, ромб, трапеция и многие другие. В прямоугольнике и квадрате диагональ делит фигуру на два равных прямоугольных треугольника, а в ромбе и трапеции диагонали соединяют вершины таким образом, что разделяют фигуру на пары равных треугольников.

Диагонали в некоторых фигурах, например, в ромбе и квадрате, обладают особыми свойствами. Например, в каждом ромбе все диагонали являются взаимно перпендикулярными, а в каждом квадрате все диагонали равны между собой.

ФигураОписаниеСвойства диагоналей

Прямоугольник	Фигура с противоположными параллельными сторонами и прямыми углами.	Диагональ делит фигуру на два равных прямоугольных треугольника.
Квадрат	Фигура с четырьмя равными сторонами и прямыми углами.	Все диагонали равны между собой.
Ромб	Фигура с четырьмя равными сторонами и противоположными равными углами.	Все диагонали взаимно перпендикулярны.
Трапеция	Фигура с двумя параллельными сторонами.	Диагонали соединяют вершины таким образом, что разделяют фигуру на пары равных треугольников.

Видео по теме:

Геометрическое свойство диагонали

Одно из главных свойств диагонали заключается в том, что она является наибольшей диагональю в многоугольнике. Другими словами, диагональ, соединяющая две самые удаленные вершины, имеет наибольшую длину по сравнению с остальными диагоналями.

Геометрическое свойство диагонали позволяет использовать ее для нахождения различных характеристик многоугольника, таких как площадь, периметр и углы. Например, с помощью диагоналей можно вычислить площадь многоугольника, разбив его на треугольники и суммируя их площади.

Также диагонали многоугольника могут быть использованы для определения некоторых его свойств, таких как симметрия и взаимное расположение вершин. Например, если диагональ делит многоугольник на два равных треугольника, то можно сделать вывод о его осевой симметрии.

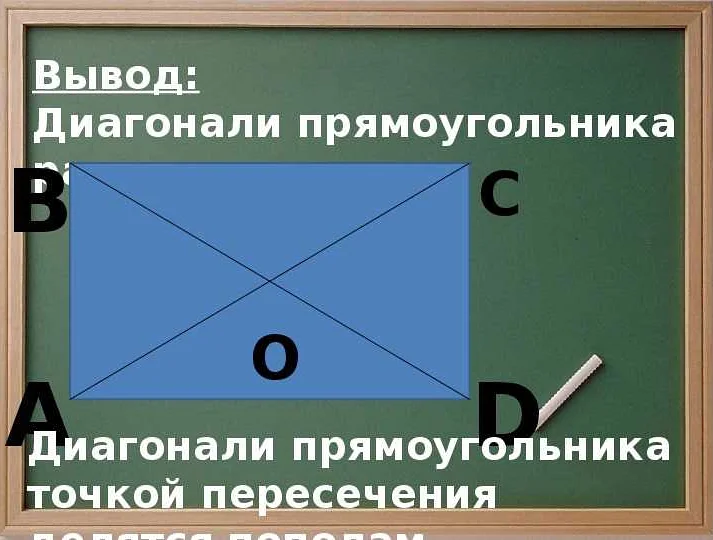
Диагональ в прямоугольнике и квадрате

В прямоугольнике диагональ делит фигуру на два прямоугольных треугольника, которые являются подобными. Это свойство позволяет находить длину диагонали, зная длины сторон прямоугольника по теореме Пифагора.

В квадрате диагональ является стороной равностороннего треугольника, образованного диагональю и двумя сторонами квадрата. Длина диагонали в квадрате можно найти, зная длину стороны квадрата по теореме Пифагора.

Прямоугольник	Квадрат

Свойства диагонали в многоугольниках

1. Количество диагоналей: В n-угольнике (многоугольнике с n вершинами) количество диагоналей равно n(n-3)/2. Например, в треугольнике (n=3) нет диагоналей, в четырехугольнике (n=4) есть две диагонали, в пятиугольнике (n=5) их уже пять, и так далее.

2. Пересечение диагоналей: Диагонали в многоугольнике могут пересекаться внутри него. Количество точек пересечения зависит от количества вершин многоугольника. Например, в треугольнике нет пересечений диагоналей, в четырехугольнике есть одно пересечение, в пятиугольнике их уже два, и так далее.

3. Длина диагонали: Длина диагонали зависит от длин сторон и углов многоугольника. В некоторых случаях можно применить теорему косинусов для нахождения длины диагонали. Однако, в общем случае, для нахождения длины диагонали необходимо провести соответствующие измерения или использовать геометрические свойства многоугольника.

Знание свойств диагонали в многоугольниках позволяет лучше понять и анализировать их форму и структуру, а также применять их в решении различных задач и проблем. Изучение диагоналей многоугольников имеет важное значение в геометрии и математике в целом.

Диагональ в треугольнике

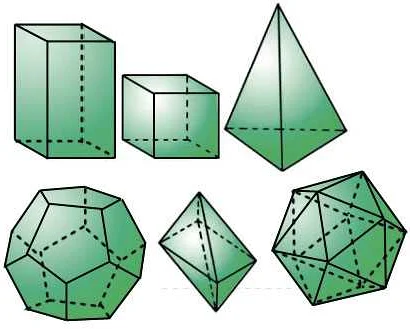
В треугольнике диагональю называется отрезок, соединяющий две вершины, не являющиеся соседними. Диагональ делит треугольник на два треугольника меньшей площади.

Диагональ в треугольнике обладает следующими свойствами:

1. Длина диагонали меньше суммы длин двух сторон, образующих треугольник: d < a + b, где d — длина диагонали, a и b — длины сторон треугольника.

2. Длина диагонали больше модуля разности длин двух сторон: d > |a — b|.

3. Диагональ может быть наибольшей стороной треугольника.

4. Диагональ может быть наименьшей стороной треугольника.

5. Диагональ может быть равна одной из сторон треугольника, что означает, что треугольник является вырожденным.

Примеры:

1. В прямоугольном треугольнике диагональ является гипотенузой.

2. В равностороннем треугольнике все стороны равны, следовательно, диагонали равны сторонам треугольника.

3. В равнобедренном треугольнике, диагональ, соединяющая вершину с основанием, разделяет треугольник на два прямоугольных треугольника.

Примеры использования диагоналей

Диагонали широко используются в различных областях математики и науки. Вот несколько примеров:

1. Геометрия: В геометрии диагонали играют важную роль при вычислении периметра и площади фигур. Например, в прямоугольнике диагональ делит его на два равных треугольника.
2. Графы: В теории графов диагонали используются для определения связей между вершинами. Например, в графе диагонали могут представлять пути или ребра, соединяющие вершины.
3. Матрицы: В матрицах диагонали играют особую роль. Главная диагональ матрицы — это линия, соединяющая левый верхний и правый нижний элементы матрицы. Второстепенная диагональ — это линия, соединяющая правый верхний и левый нижний элементы матрицы.
4. Физика: В физике диагонали могут использоваться для описания траекторий движения объектов или для определения направления сил.
5. Кристаллография: В кристаллографии диагонали могут помочь определить структуру кристалла или направление его осей.

Это лишь некоторые примеры использования диагоналей в математике и науке. Диагонали являются важными и полезными инструментами, которые помогают нам лучше понять и описать мир вокруг нас.

Диагональ в матрицах и графах

В матрицах диагональ обозначается как главная диагональ и состоит из элементов, у которых индексы строки и столбца совпадают. Например, в матрице 3×3 элементы на главной диагонали имеют индексы (1, 1), (2, 2) и (3, 3).

В графах диагональ обозначает ребра, которые соединяют вершины с собой же. Такие ребра называются петлями. Например, если в графе имеется вершина А и у нее есть петля, то это означает, что из вершины А можно перейти в нее же саму.

Диагональные элементы в матрицах и петли в графах могут быть полезны при анализе и решении различных задач. Например, в матрицах диагональ содержит информацию о главных характеристиках системы, а в графах петли позволяют определить связность и цикличность графа.

Вопрос-ответ:

Что такое диагональ в математике?

Диагональ — это отрезок, соединяющий две вершины многоугольника, которые не являются соседними.

Каковы свойства диагоналей многоугольника?

Диагонали многоугольника обладают несколькими свойствами: сумма их длин всегда больше суммы длин сторон, они делят многоугольник на треугольники и могут быть пересечены только в вершинах.

Как найти длину диагонали многоугольника?

Длина диагонали многоугольника может быть найдена с помощью различных методов, в зависимости от известных данных. Например, если известны длина стороны многоугольника и угол между диагональю и стороной, то длину диагонали можно найти с помощью тригонометрических функций.

Какие примеры можно привести в качестве иллюстрации к понятию диагональ?

Примерами диагоналей могут служить отрезки, соединяющие вершины различных многоугольников, например, диагонали квадрата, прямоугольника или пятиугольника.

В каких случаях диагональ многоугольника может быть равна его стороне?

Диагональ многоугольника может быть равна его стороне только в случае правильного многоугольника, то есть в таком многоугольнике все стороны и углы равны.

Что такое диагональ в математике?

В математике диагональ — это отрезок, соединяющий две несоседние вершины многоугольника или прямоугольника.

Какие свойства имеет диагональ в математике?

Диагональ многоугольника делит его на два треугольника, имеет длину меньшую, чем периметр многоугольника, и является гипотенузой внутреннего прямоугольного треугольника.